The period of oscillation of a mass m suspended by an ideal spring is 2s. If an additional mass of 2 kg be suspended, the time period is increased by 1s. Find the value of m.
The correct Answer is:1.6 kg
To solve the problem, we need to find the value of the mass m suspended from an ideal spring, given the conditions of the oscillation periods.
1. Understanding the Time Period Formula:
The time period T of a mass m suspended from a spring with spring constant K is given by the formula:
T=2π√mK
From the problem, we know that the initial time period T1=2 seconds.
2. Setting Up the First Equation:
Using the time period formula for the initial mass m:
2=2π√mK
Dividing both sides by 2π:
22π=√mK
Squaring both sides gives:
(1π)2=mK
Thus, we can express m in terms of K:
m=Kπ2
3. Adding the Additional Mass:
When an additional mass of 2 kg is added, the new total mass becomes m+2. The new time period T2 is given as 3 seconds. Using the time period formula again:
3=2π√m+2K
Dividing both sides by 2π:
32π=√m+2K
Squaring both sides gives:
(32π)2=m+2K
Rearranging gives:
m+2=94π2K
4. Setting Up the System of Equations:
Now we have two equations:
1. m=Kπ2
2. m+2=94π2K
5. Substituting the First Equation into the Second:
Substitute m from the first equation into the second:
Kπ2+2=94π2K
To eliminate K, multiply through by 4π2:
4K+8π2=9K
Rearranging gives:
9K−4K=8π2
Thus:
5K=8π2
Therefore:
K=8π25
6. Finding the Value of m:
Substitute K back into the equation for m:
m=Kπ2=8π25π2=85
Therefore, the value of m is:
m=1.6 kg
Final Answer:
The value of m is 1.6 kg.
The time period T of a mass m suspended from a spring with spring constant K is given by the formula:
T=2π√mK
From the problem, we know that the initial time period T1=2 seconds.
Using the time period formula for the initial mass m:
2=2π√mK
Dividing both sides by 2π:
22π=√mK
Squaring both sides gives:
(1π)2=mK
Thus, we can express m in terms of K:
m=Kπ2
When an additional mass of 2 kg is added, the new total mass becomes m+2. The new time period T2 is given as 3 seconds. Using the time period formula again:
3=2π√m+2K
Dividing both sides by 2π:
32π=√m+2K
Squaring both sides gives:
(32π)2=m+2K
Rearranging gives:
m+2=94π2K
Now we have two equations:
1. m=Kπ2
2. m+2=94π2K
Substitute m from the first equation into the second:
Kπ2+2=94π2K
To eliminate K, multiply through by 4π2:
4K+8π2=9K
Rearranging gives:
9K−4K=8π2
Thus:
5K=8π2
Therefore:
K=8π25
Substitute K back into the equation for m:
m=Kπ2=8π25π2=85
Therefore, the value of m is:
m=1.6 kg
The value of m is 1.6 kg.
Topper's Solved these Questions
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise
233 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Problem
23 Videos
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66 Videos
- Physical worldBOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise
49 Videos
Similar Questions
A period of oscillation of a mass m kg is suspended by an ideal spring is 1.5s. If an additional mass 3kg be suspended, the time period is increased by 1s. Find the value of m.
View SolutionA mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.
View Solution
Knowledge Check
If the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
A1sB2sC3sD4sIf the period of oscillation of mass M suspended from a spring is one second, then the period of 4M will be
A1/2 sB1/4 sC2 sD4sThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
ATBT/√2C2TD√2T

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionThe period of oscilation of a mass M suspended a spring negligible mass is T if along with it and there mass M is also suspended the period of oscillation now be
View SolutionWhen a mass m attached to a spring it oscillates with period 4s. When an additional mass of 2 kg is attached to a spring, time period increases by 1s. The value of m is :-
View SolutionA mass m attached to a light spring oscillates with a period of 2 s. If the mass is increased by 2 kg, the period increases by 1 s. Then the value of m is
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
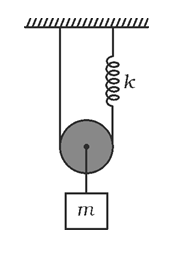
View Solution
