The periodic times of oscillation of a dip needle in two perpendicular vertical planes are t1 and t2 respectively. If the periodic time of the same needle in the magnetic meridian is t, showthat
1t41+1t42=1t4(1+sin2δ)
where δ is the angle of dip.
Step by step video & image solution for The periodic times of oscillation of a dip needle in two perpendicular vertical planes are t_(1) and t_(2) respectively. If the periodic time of the same needle in the magnetic meridian is t, showthat (1)/(t_(1)^(4))+(1)/(t_(2)^(4))=(1)/(t_(4))(1+sin^(2)delta ) where delta is the angle of dip. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETISMBook:SL ARORAChapter:MAGNETISMExercise:Based on Coulomb s law and dipole moment of a magnet
Explore 5 Videos
- MAGNETISMBook:SL ARORAChapter:MAGNETISMExercise:Based on Torque and potential energy of dipole in magnetic field
Explore 14 Videos
- MAGNETISMBook:SL ARORAChapter:MAGNETISMExercise:Based on (i) Earth s Magnetism (ii) magnetic field of a bar magnet
Explore 60 Videos
- MAGNETIC EFFECTS OF CURRENTBook:SL ARORAChapter:MAGNETIC EFFECTS OF CURRENTExercise:TYPE C
Explore 4 Videos
- OPTICAL INSTRUMENTSBook:SL ARORAChapter:OPTICAL INSTRUMENTSExercise:Problems for self practice
Explore 35 Videos
Similar Questions
The period of oscillation of a dip needle when vibrating in the magnetic meridian is 1.5s. In a plane at right angles to the magnetic meridian it is 2s. Find the dip of the place
View SolutionThe bae of a triangle is divided into three equal parts. If t1,t2,t3 be the tangent sof the angles subtended by these parts at the opposite vertex, prove that :
(1t1+1t2)(1t1+1t3)=4(1+1t21)
View Solution
Knowledge Check
A binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
AT1>T2 if R1>R2BT1>T2 if M1>M2CT1=T2DT1T2=(R1R2)3/2The period of oscillation of compass needle is 8 s at a place where dip angle is 30∘ and magnetic field is B1 . At another place where dip angle is 60∘ and magnetic field is B2 , the period of oscillation is 4 is then B2B1 is
A4√3B3√3C57D87The decay constant of radio isotope is λ. If A1andA2 are its activities at times t1andt2 respectively, the number of nuclei which have decayed during the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)
The base of a triangle is divided into three equal parts. If t1,t2,t3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1t1+1t2)(1t2+1t3)=4(1+1t22).
View SolutionFind the are of triangle whose vertex are: (at1,at1)(at2,at2)(at3,at3)
View Solutionshows an oscillating pendulum.
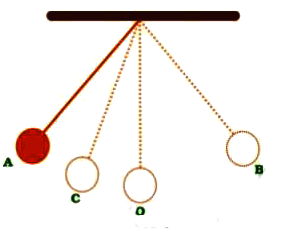
Time taken by the bob to move from A to C is t1 and from C to O is t2. The time period of this simple pendulum is
View SolutionIf T and T' are the periods of a simple pendulum and a conical pendulum of the sample length then .
View SolutionTwo planets move around the sun. The periodic times and the mean radii of the orbits are T1,T2 and r1r2 respectively. The ratio T1/T2 is equal to
View Solution