The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
The correct Answer is:3
To solve the problem, we need to analyze the relationship between power, force, and the velocity of a particle moving in a straight line, given that the velocity varies with displacement as x(1/K).
1. Understanding Power:
Power (P) is defined as the work done per unit time. Mathematically, it can be expressed as:
P=Wt=F⋅v
where F is the force acting on the particle and v is its velocity.
2. Expressing Force:
The force can also be expressed using Newton's second law:
F=m⋅a
where m is the mass of the particle and a is its acceleration.
3. Relating Acceleration and Velocity:
We know that acceleration a can be expressed in terms of velocity v and displacement s using the kinematic equation:
a=dvdt=dvds⋅dsdt=dvds⋅v
Therefore, we can write:
a=vdvds
4. Substituting into Power Equation:
Substituting a into the power equation gives:
P=m⋅(vdvds)⋅v=mv2dvds
5. Constant Power:
Since the power P is constant, we can express it as:
P=mv2dvds=constant
6. Rearranging the Equation:
Rearranging the equation gives:
v2dvds=Pm=constant
7. Integrating:
Let C=Pm (a constant). We can write:
v2dv=Cds
Integrating both sides:
∫v2dv=∫Cds
This results in:
v33=Cs+C1
where C1 is the constant of integration.
8. Expressing Velocity in Terms of Displacement:
Rearranging gives:
v3=3Cs+3C1
This shows that v3 is proportional to s:
v3∝s
9. Relating to Given Expression:
We are given that v∝s(1/K). From our result, we have:
v∝s1/3
This implies:
1K=13⟹K=3
Final Answer:
The value of K is 3.
Power (P) is defined as the work done per unit time. Mathematically, it can be expressed as:
P=Wt=F⋅v
where F is the force acting on the particle and v is its velocity.
The force can also be expressed using Newton's second law:
F=m⋅a
where m is the mass of the particle and a is its acceleration.
We know that acceleration a can be expressed in terms of velocity v and displacement s using the kinematic equation:
a=dvdt=dvds⋅dsdt=dvds⋅v
Therefore, we can write:
a=vdvds
Substituting a into the power equation gives:
P=m⋅(vdvds)⋅v=mv2dvds
Since the power P is constant, we can express it as:
P=mv2dvds=constant
Rearranging the equation gives:
v2dvds=Pm=constant
Let C=Pm (a constant). We can write:
v2dv=Cds
Integrating both sides:
∫v2dv=∫Cds
This results in:
v33=Cs+C1
where C1 is the constant of integration.
Rearranging gives:
v3=3Cs+3C1
This shows that v3 is proportional to s:
v3∝s
We are given that v∝s(1/K). From our result, we have:
v∝s1/3
This implies:
1K=13⟹K=3
The value of K is 3.
Topper's Solved these Questions
Similar Questions
The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
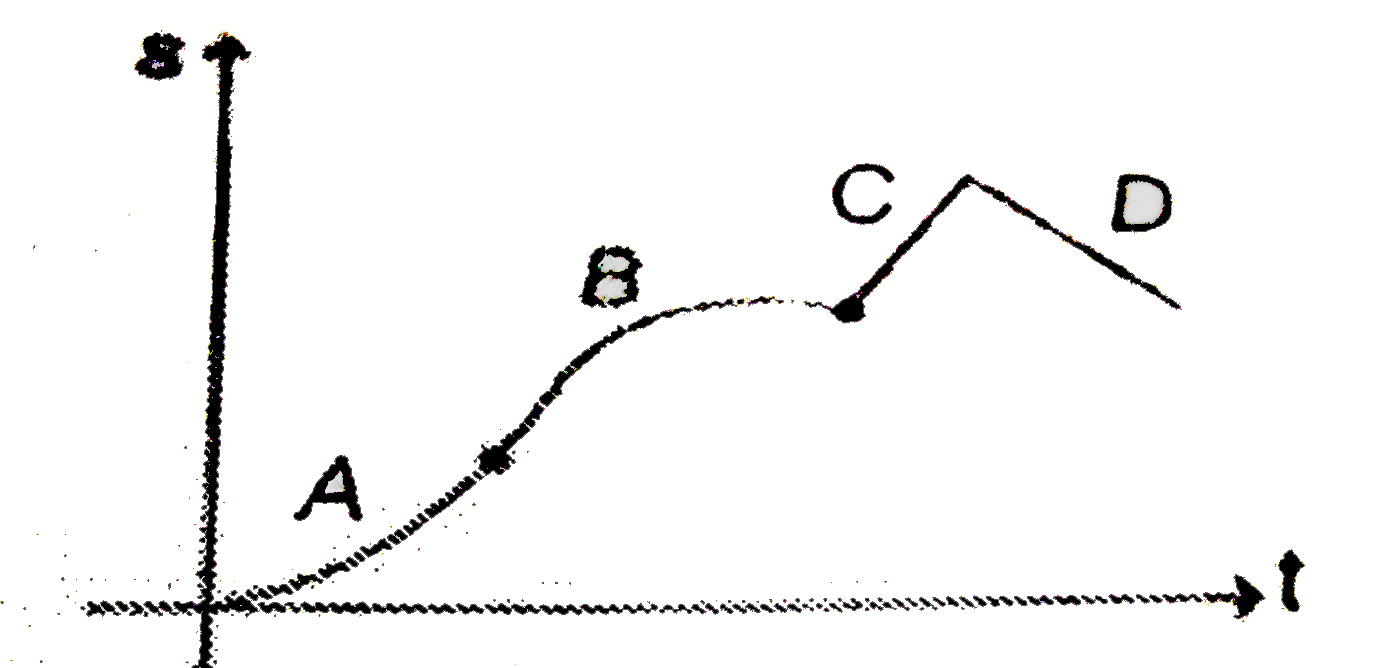
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.

The acceleration of the particle.
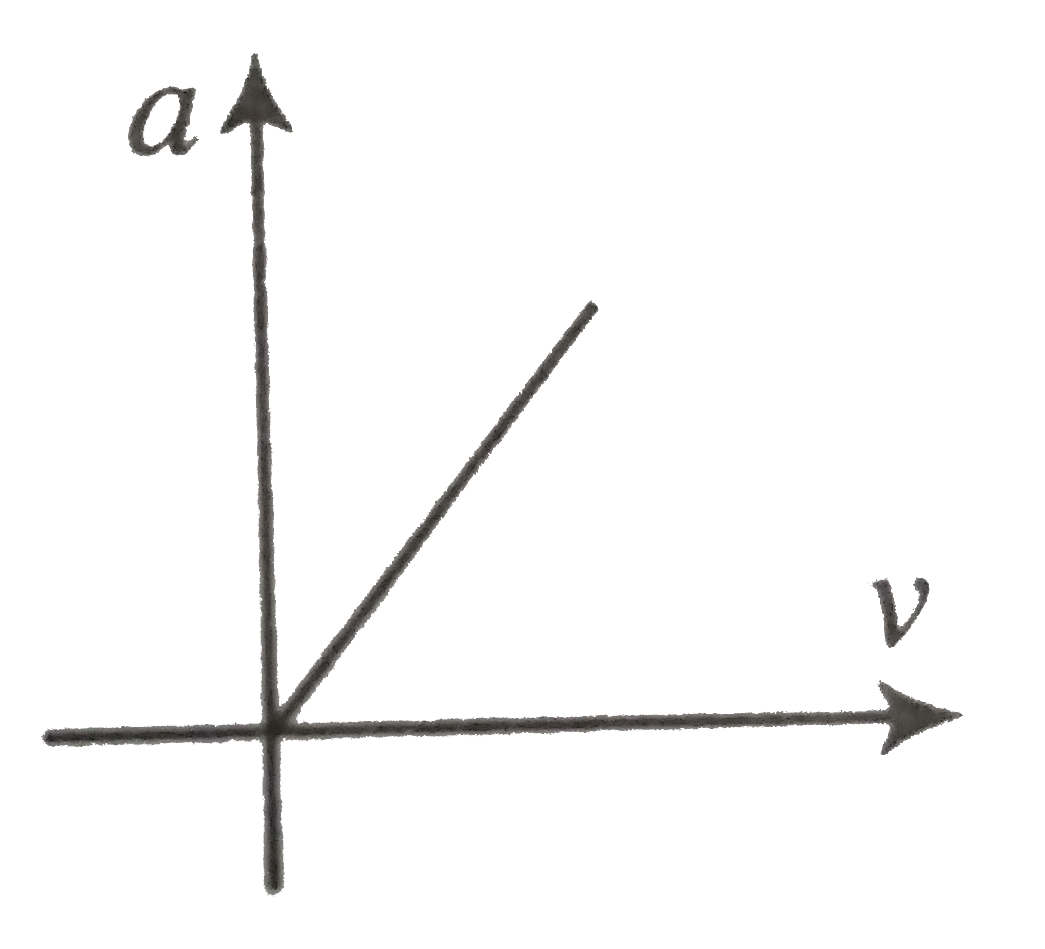
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
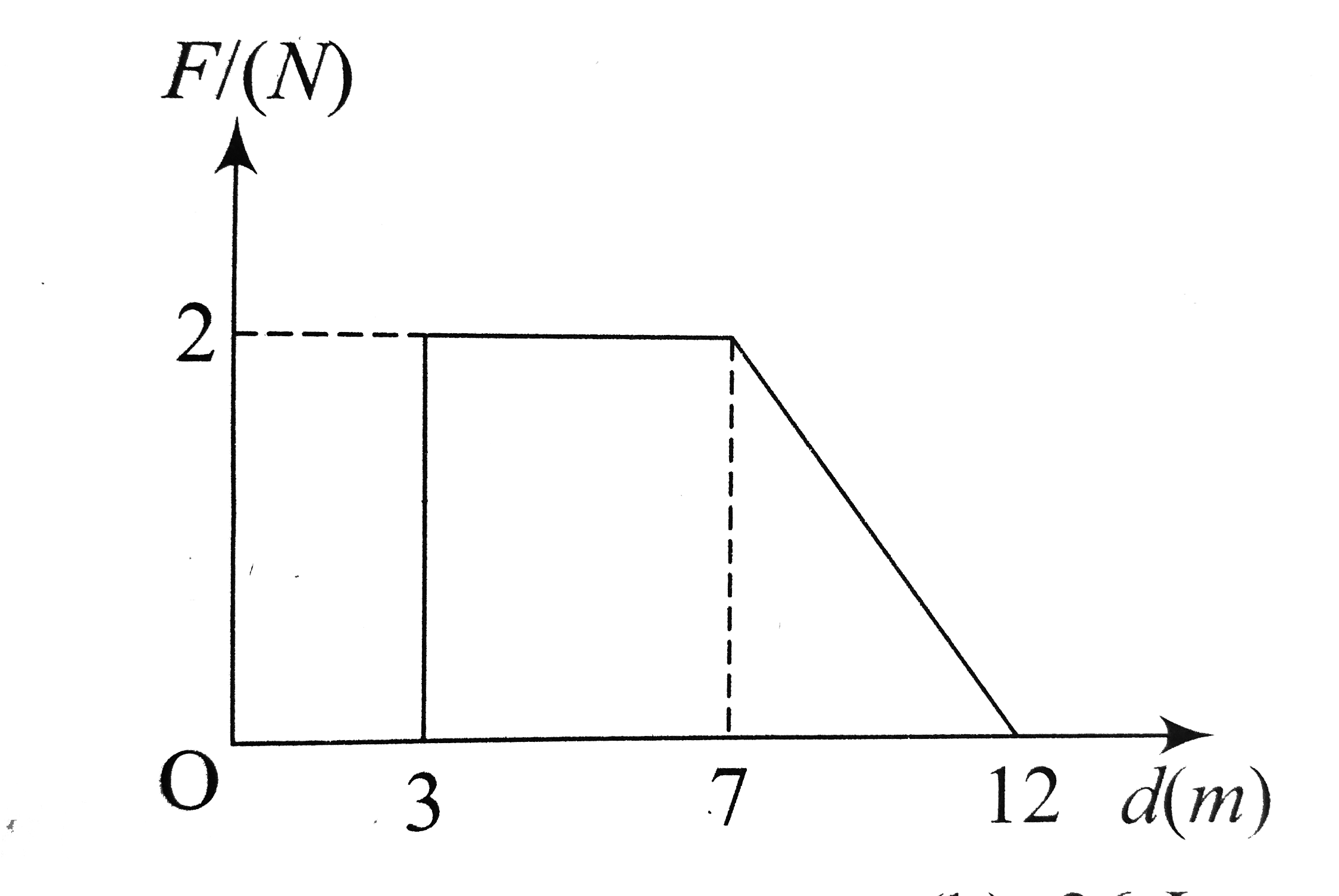
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
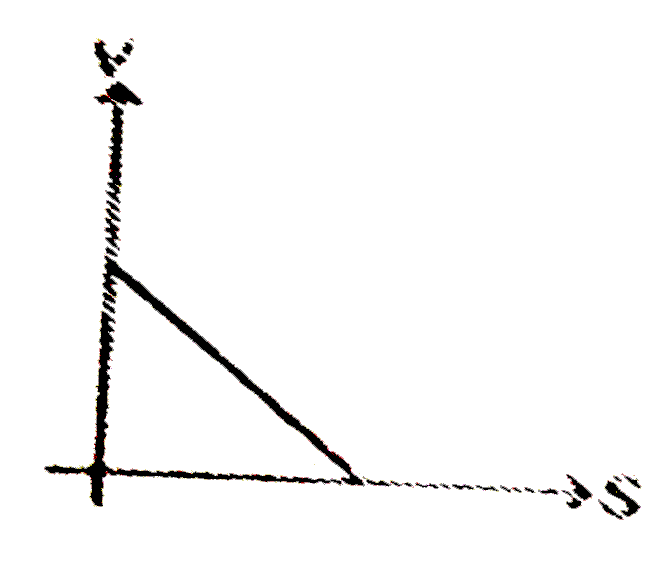
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
View SolutionGraph of velocity versus displacement of a particle moving in a straight line is as shown in figure.
The acceleration of the particle is.
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View Solution