The pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor. (Take : density of water = 1000kg m−3,g=10m s−2 )
To find the height of the first floor based on the given pressures, we can follow these steps:
Step 1: Understand the relationship between pressure, height, and density
The pressure difference between two points in a fluid can be expressed using the formula:
ΔP=ρgh
where:
- ΔP is the difference in pressure,
- ρ is the density of the fluid,
- g is the acceleration due to gravity,
- h is the height difference.
Step 2: Calculate the difference in pressure
Given:
- Pressure on the ground floor, P1=40,000Pa
- Pressure on the first floor, P2=10,000Pa
The difference in pressure (ΔP) is:
ΔP=P1−P2=40,000Pa−10,000Pa=30,000Pa
Step 3: Substitute the known values into the pressure formula
We can rearrange the pressure formula to solve for height h:
h=ΔPρg
Substituting the known values:
- ΔP=30,000Pa
- ρ=1000kg/m3
- g=10m/s2
We get:
h=30,000Pa1000kg/m3×10m/s2
Step 4: Calculate the height
Now, calculating the height:
h=30,00010,000=3m
Final Answer
The height of the first floor is 3m.
---
The pressure difference between two points in a fluid can be expressed using the formula:
ΔP=ρgh
where:
- ΔP is the difference in pressure,
- ρ is the density of the fluid,
- g is the acceleration due to gravity,
- h is the height difference.
Given:
- Pressure on the ground floor, P1=40,000Pa
- Pressure on the first floor, P2=10,000Pa
ΔP=P1−P2=40,000Pa−10,000Pa=30,000Pa
We can rearrange the pressure formula to solve for height h:
h=ΔPρg
- ΔP=30,000Pa
- ρ=1000kg/m3
- g=10m/s2
h=30,000Pa1000kg/m3×10m/s2
Now, calculating the height:
h=30,00010,000=3m
The height of the first floor is 3m.
Topper's Solved these Questions
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (4 Marks Questions )
10 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (2 Marks Questions )
45 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (4 Marks Questions )
16 Videos
- ELECTRICITY AND MAGNETISM BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )
6 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
Similar Questions
A water pump raises 50 litres of water through a height of 25 m in 5 .Calculate the power of the pump required . (Take g=10 N kg−1 and density of water =1000 kg m−3)
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View Solution
Knowledge Check
At What velocity does water emerge from an orifice in a tank in which gauge pressure is 3×105Nm−2 before the flow starts ? (Take the density of water =1000kgm−3.)
A24.5ms−1B14.5ms−1C34.5ms−1D44.5ms−1A drop of water of radius 0.0015 mm is falling in air .If the cofficient of viscosity of air is 2.0×10−5kgm−1s−1 ,the terminal velocity of the drop will be
(The density of water = 103kgm−3 and g = 10ms−2 )A1. 1.0×10−4ms−1B2. 2.0×10−4ms−1C3. 2.5×10−4ms−1D4. 5.0×10−4ms−1
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
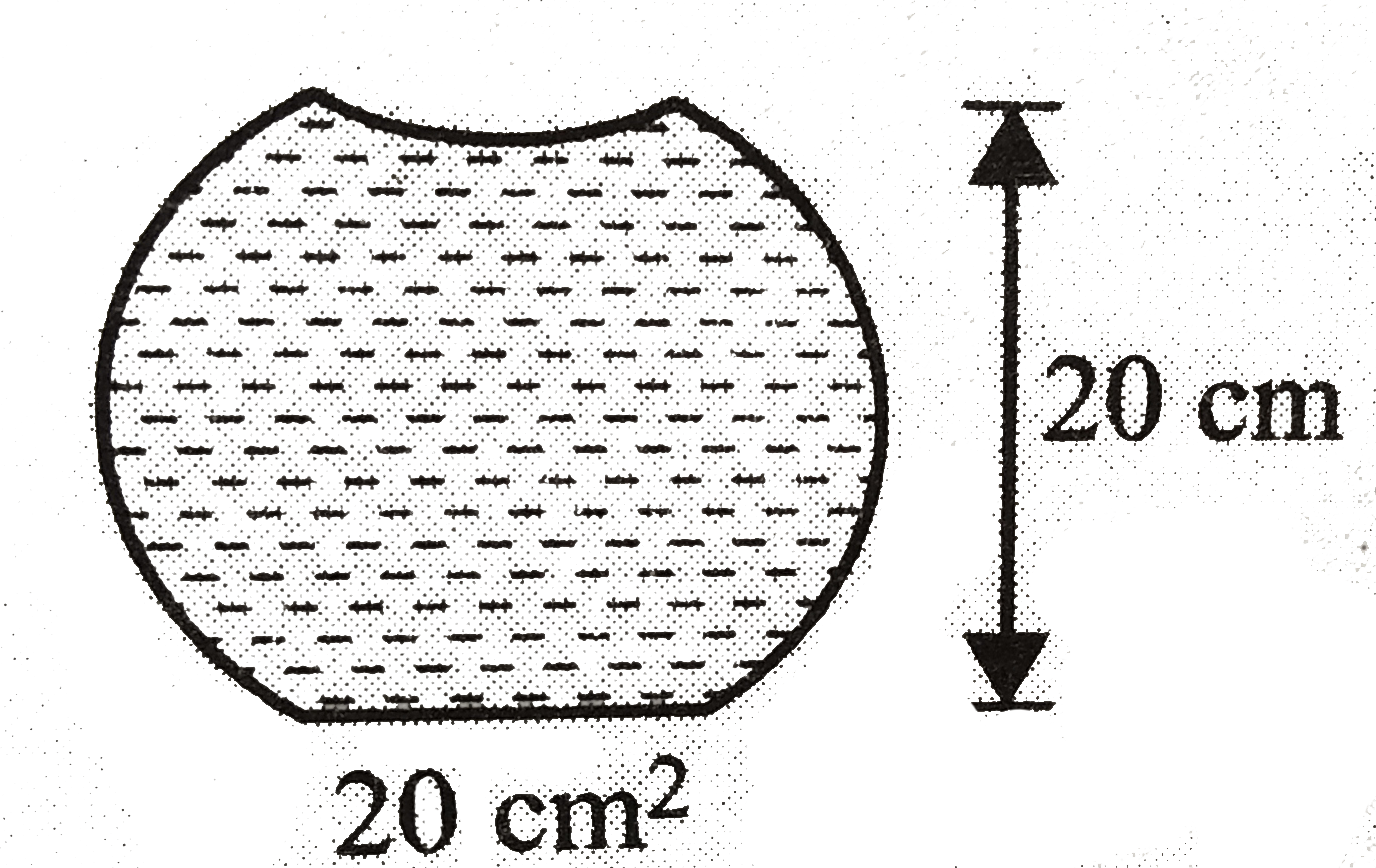
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionThe rate of water gushing out of a pipe of radius 5 cm is 100Lmin−1. The Reynolds number for the flow is of the orderof [density of water = 1000kgm−3 ,coefficient of viscosity of water = 1m Pa s ]
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View Solution
