The pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

Let in equilibrium extension of spring is x0, tension in spring is T=kx0

mg=2T=2kx0
x0=mg2k
After equilibrium position, pulley goes down by x, spring extends by 2x.
The energy of the system is
E=12mv2+12Iω2−mgx+12k(x0+2x)2
=12mv2+12Iv2r2−mgx+12k(x0+2x)2
Since total energy is constant
dEdt=0
0=12(m+Ir2)2vdvdt−mg(dxdt)
+12k⋅2(x0+2x)2dxdt
=(m+Ir2)va−mgv+2k(x0+2x)v
=(m+Ir2)a−mg+2kx0+4kx
(m+Ir2)a=−4kx
a=−4k(m+I/r2)x=−ω2x
T=2π√m+I/r24k
Topper's Solved these Questions
Similar Questions
The pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.
 View Solution
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
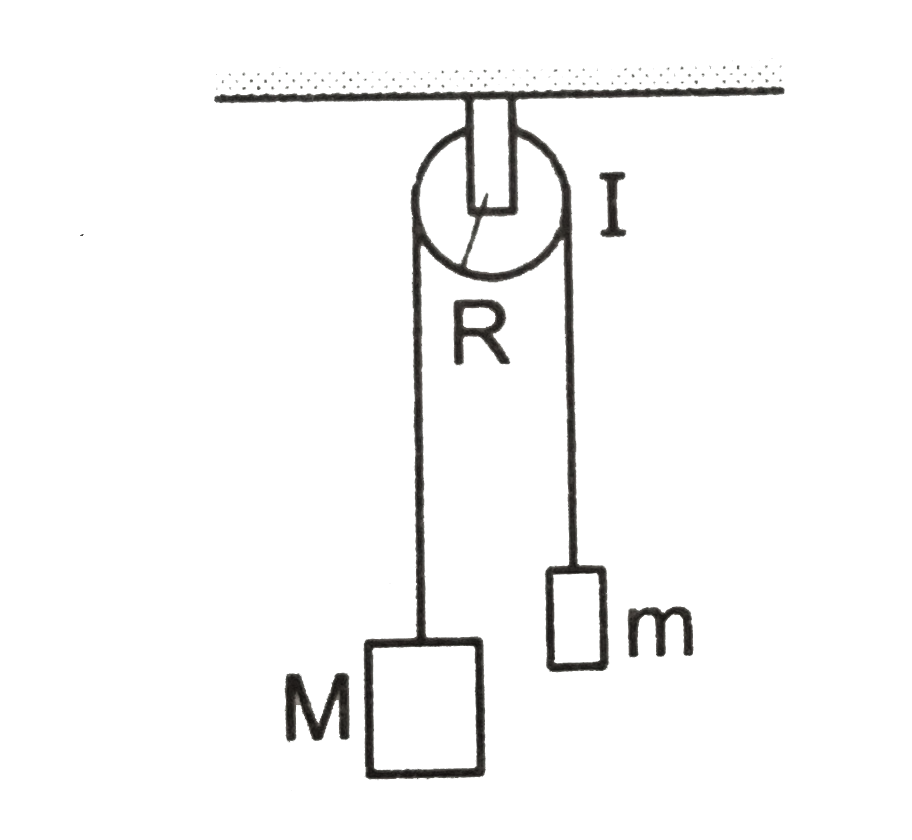 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k - Question 2 - Select One
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
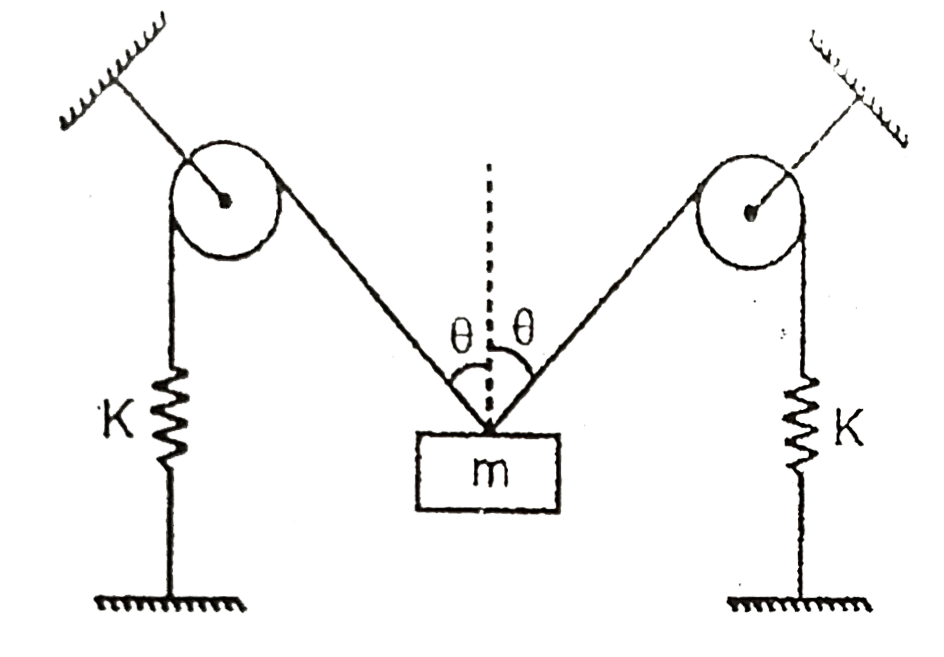 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k - Question 3 - Select One
An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
AA√k/mBA2k/mCA√m/kDAm/k
Figure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
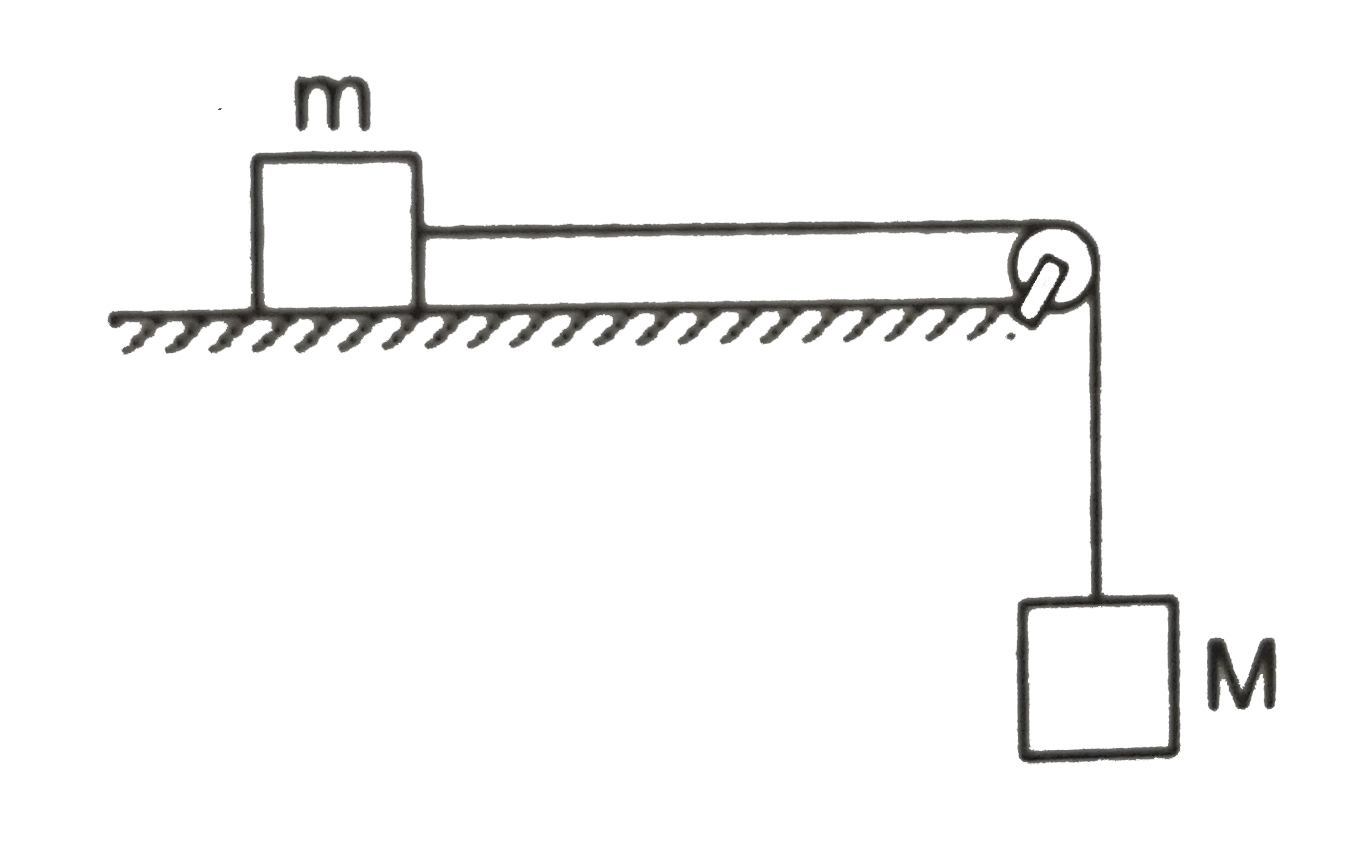 View Solution
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
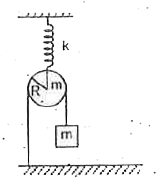 View Solution
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
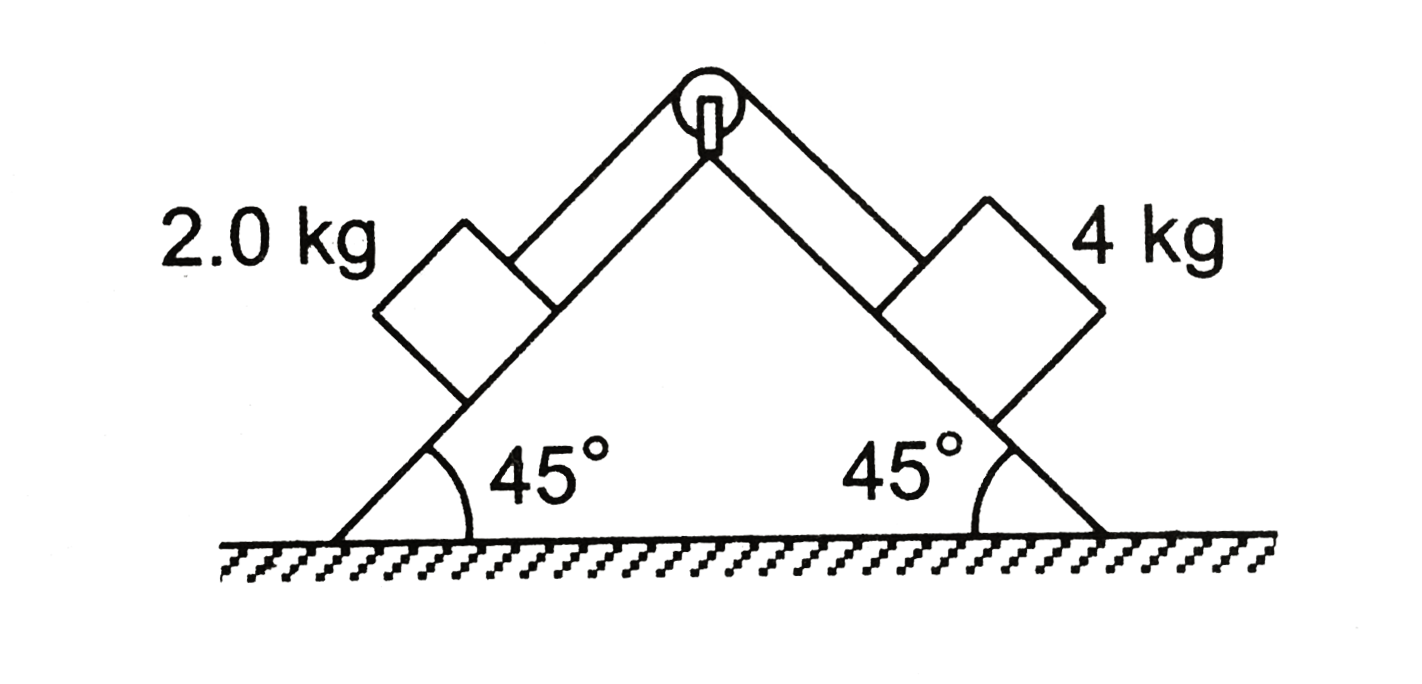 View Solution
View SolutionFind the frequency of small oscillations of the arrangement illustrated in figure. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x.The mass of the thread and the spring is negligible , the thread does not slide over the pulley, there is no friction in the axis of the pulley
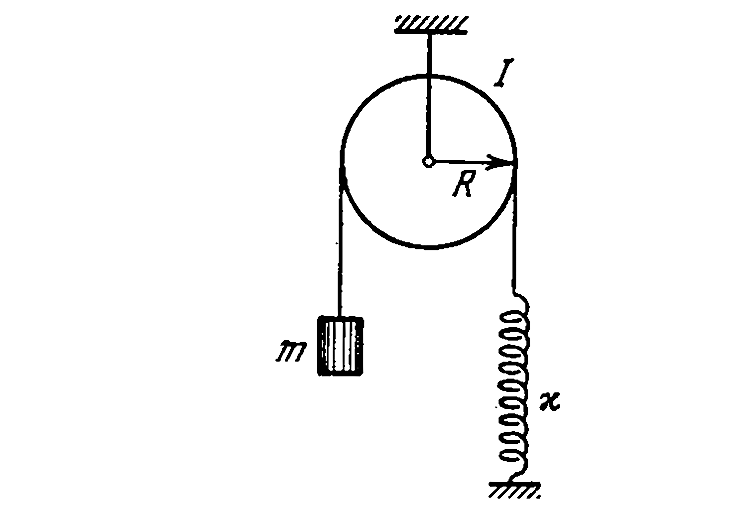 View Solution
View Solution

