Consider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
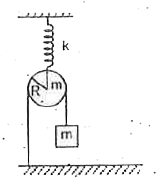
At equilibrium position let be the deformation in the spring
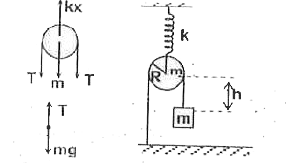
Let the pulley is displaced by x then total energy of system
As string does not slip over pulley so .
So
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - COMPREHENSION
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
The pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

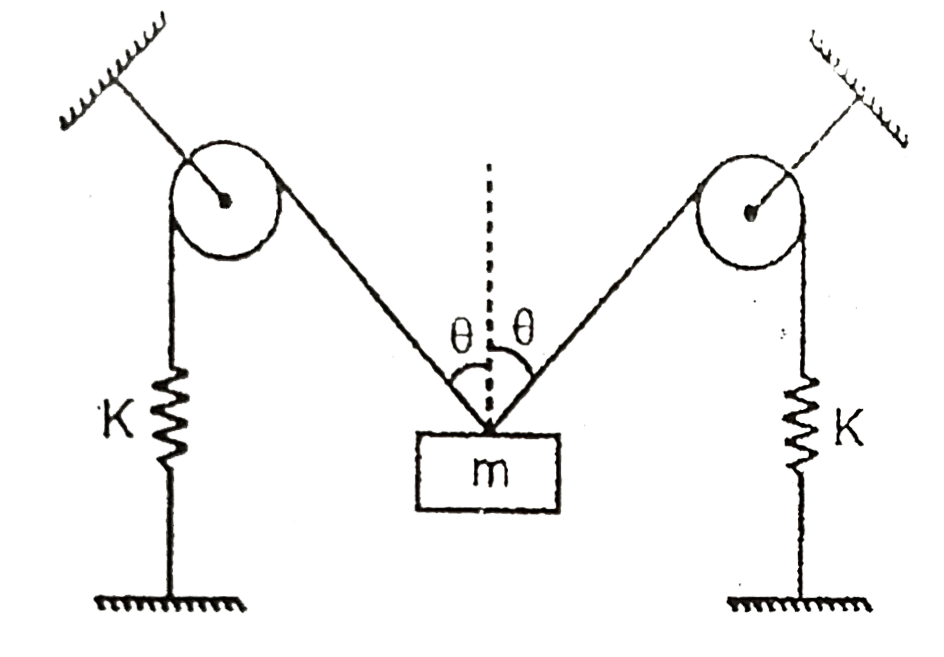
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
View Solution
Knowledge Check
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
The string, the spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionThe pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionThe time period of block of mass m is (Assume pulleys and string are massless)
_PHY_E06_345_Q01.png) .
.
View Solution
