Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
The correct Answer is:B
Let us slove the problem by energy method, iniltial extension of the spring in the mean position δ=mgk
During oscilating at ny positin x below the equlibrium positon let tehh velocilty of m be v and angular velocity of the puley be omega. If r is the radius of the pulley, then
v=rω
At any instant total energy
=constant (For SHM)
∴12mv2+12Iω2+12k[(x+δ)2−δ2]−mgx
=constant
→(12mv2+(12)Iω2+(12)kx2+kxd−mgx ltbrgeconstant
→(12)mv2+(12)1(v2+r2)+(12)kx2
=constant (δ=mgk)
Taking derivative of both sides with respect of t
mv.dvdt1r2v.dvdt+kxdxdt=0
→a(m+1r2)=−kx
⟨.=dxdtanda=dvdt)
→ar=km+1r2=ω2
→T=2π
⎷m+1r2k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Figure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
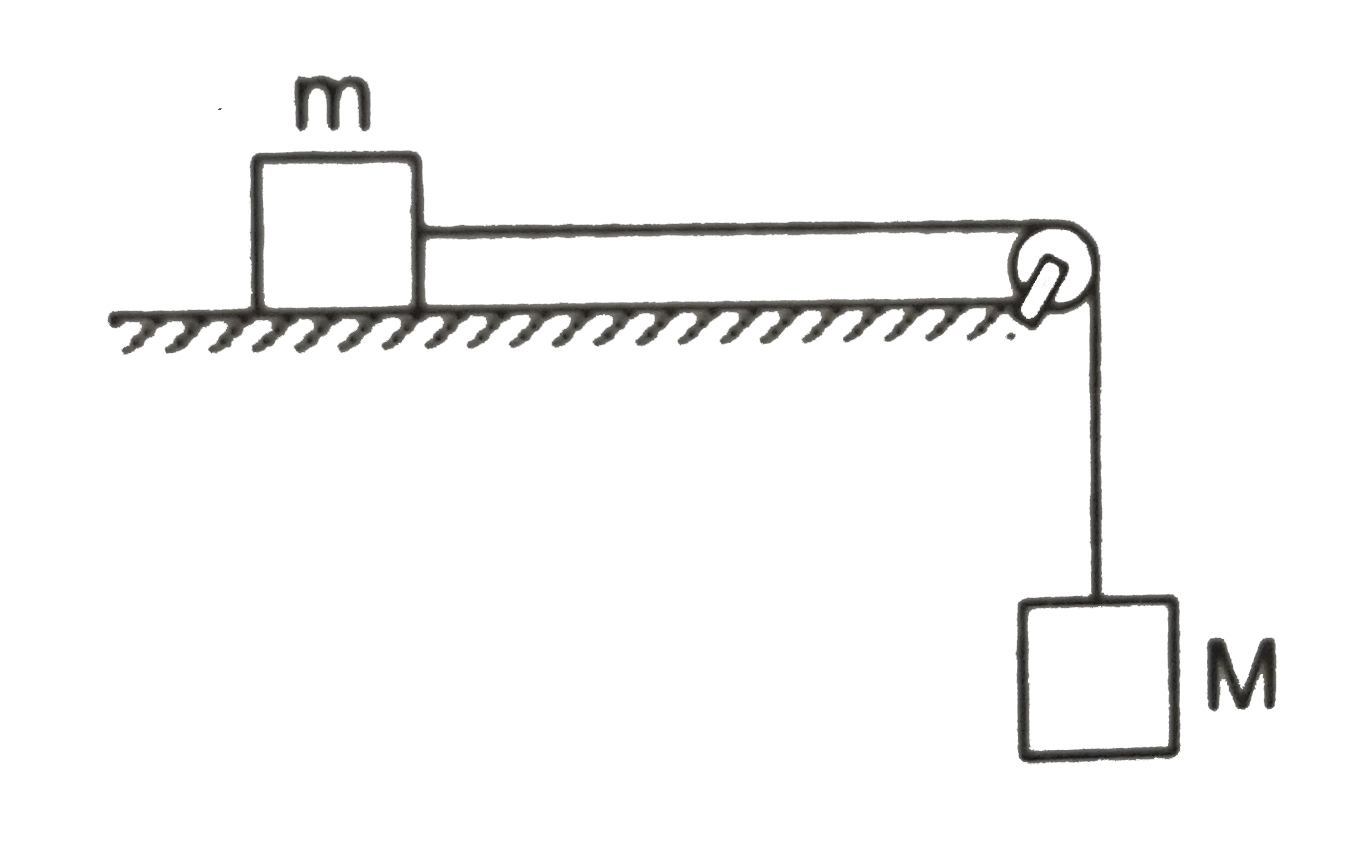
View SolutionFigure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.

View Solution
Knowledge Check
Consider two masses with m1>m2 connected by a light inextensible string that passes over a pulley of radius R and moment of inertia I about its axis of rotation. The string does not slip on the pulley and the pulley turns without friction. The two masses are released from rest separated by a vertical distance 2h. When the two masses pass each other, the speed of the masses is proportional to
A ⎷m1−m2m1+m2+1R2B ⎷(m1−m2)(m1−m2)m1+m2+1R2C ⎷m1+m2+1R2m1−m2D ⎷1R2m1+m2Consider two object with m1>m2 connected by a light string that passes over a pulley having a moment of inertia of I about its axis of rotation as shown in figure. The string does not slip on the pulley or strech. The pulley turns without friction. The two objects are released from rest separated by a vertical distance 2h. The translational speeds of the objects as they pass each other is.
 .A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2
.A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2
A block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not realtive to the pulley. Find the frequency of small oscillations.
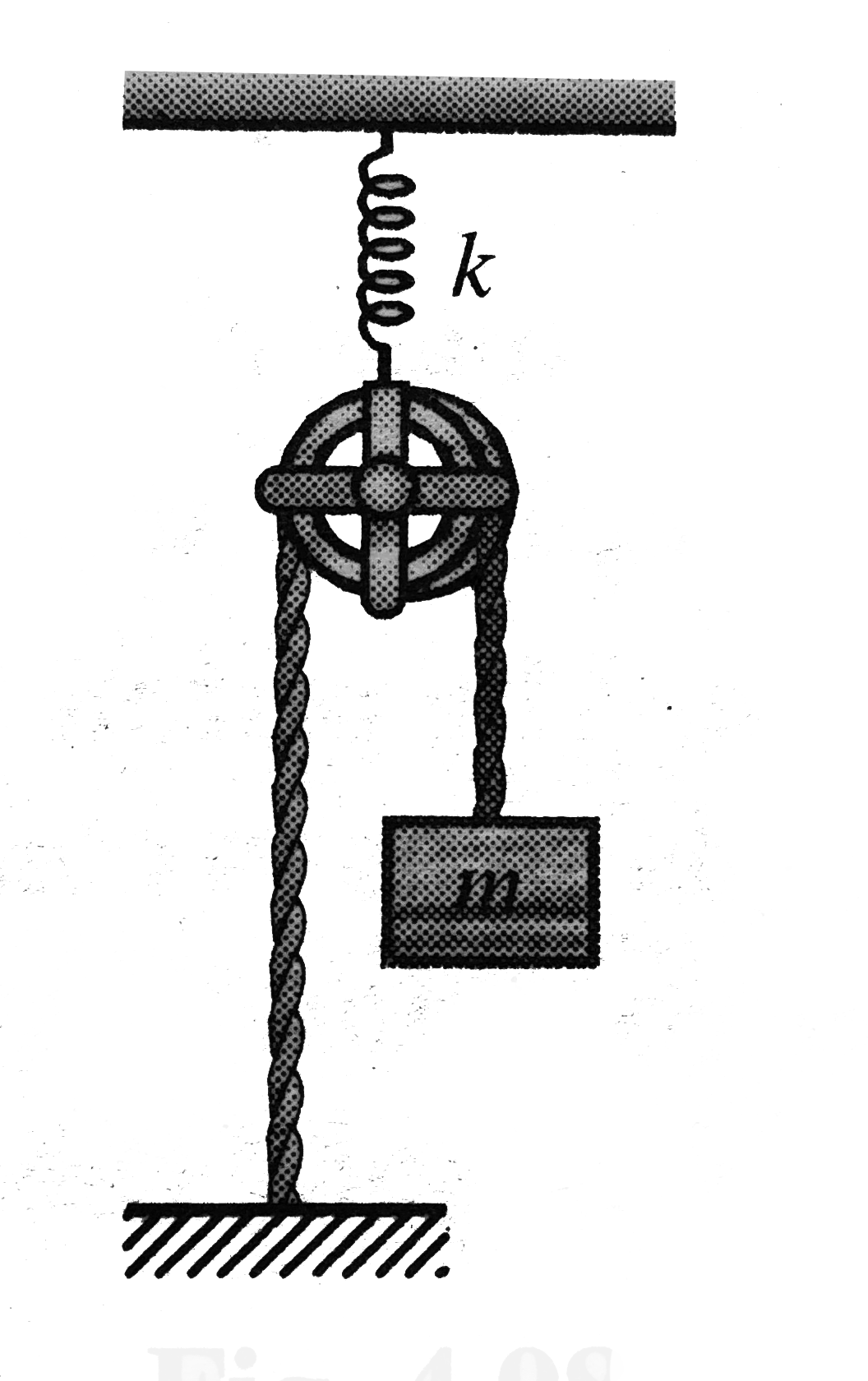
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
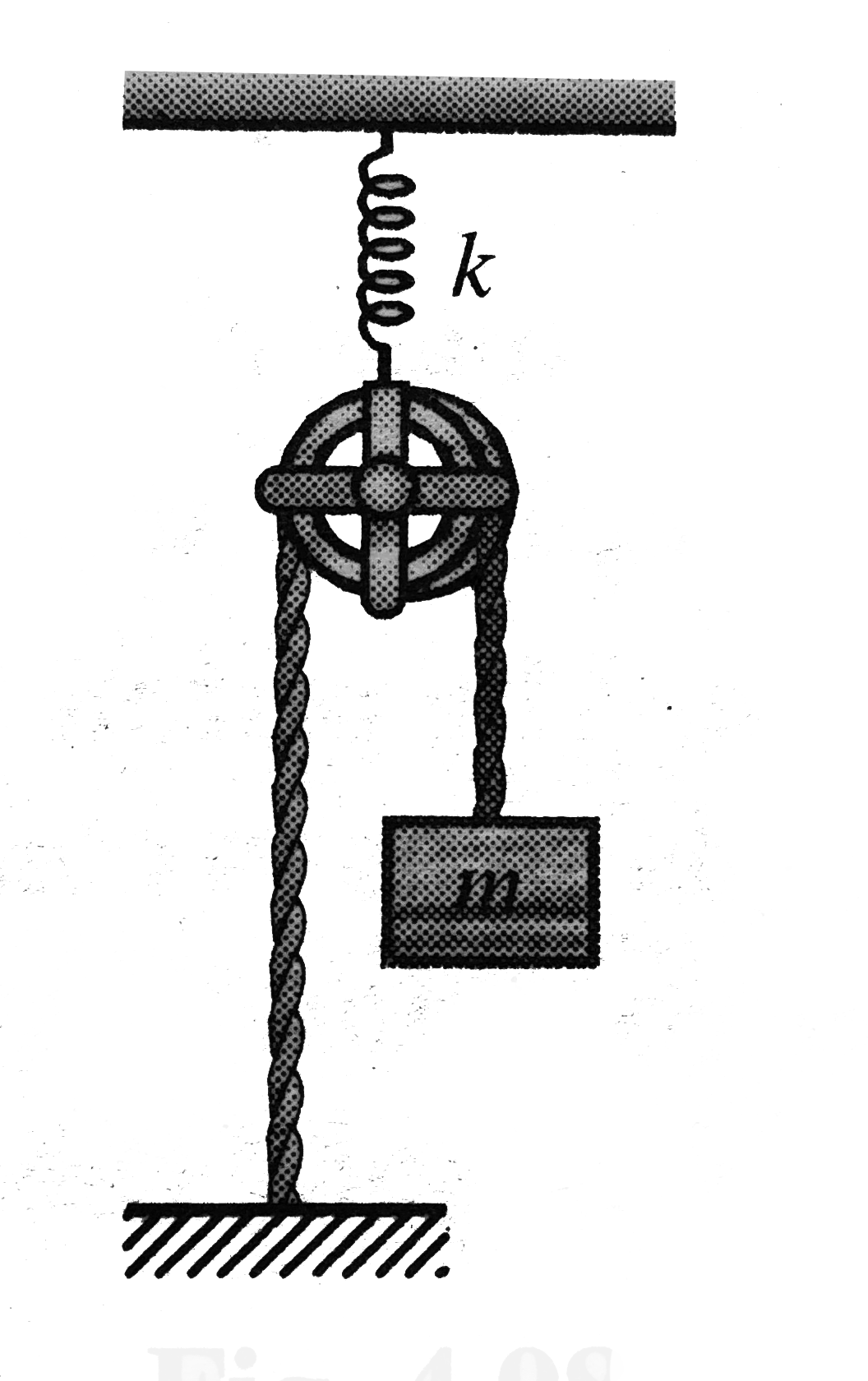
View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
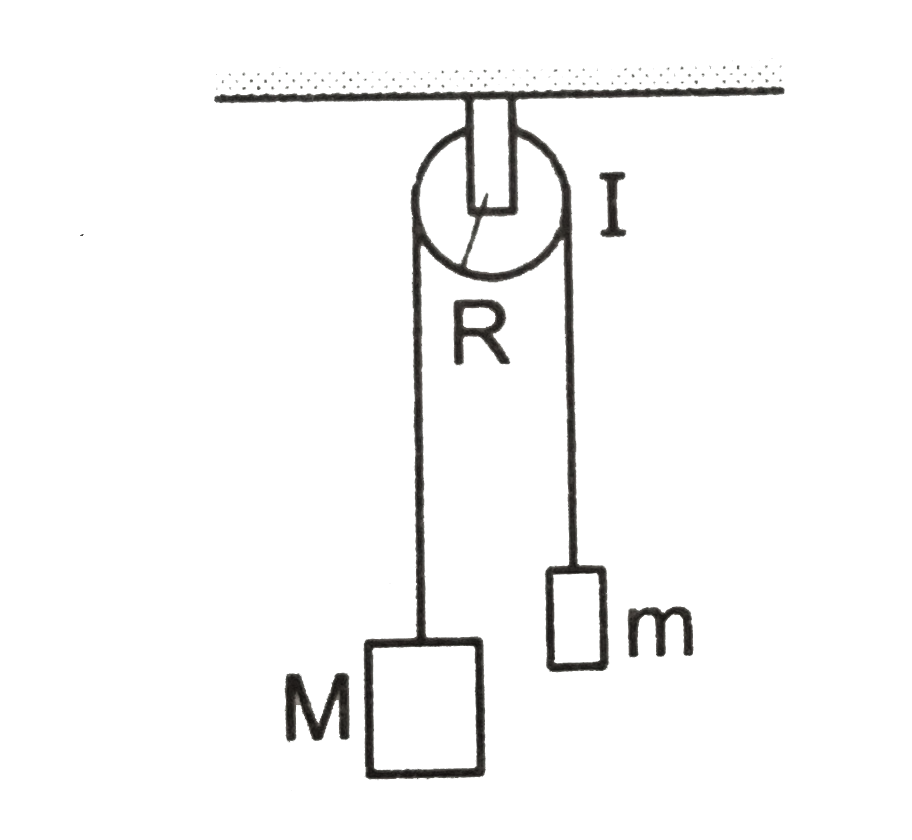
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

View SolutionThe pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View Solution
