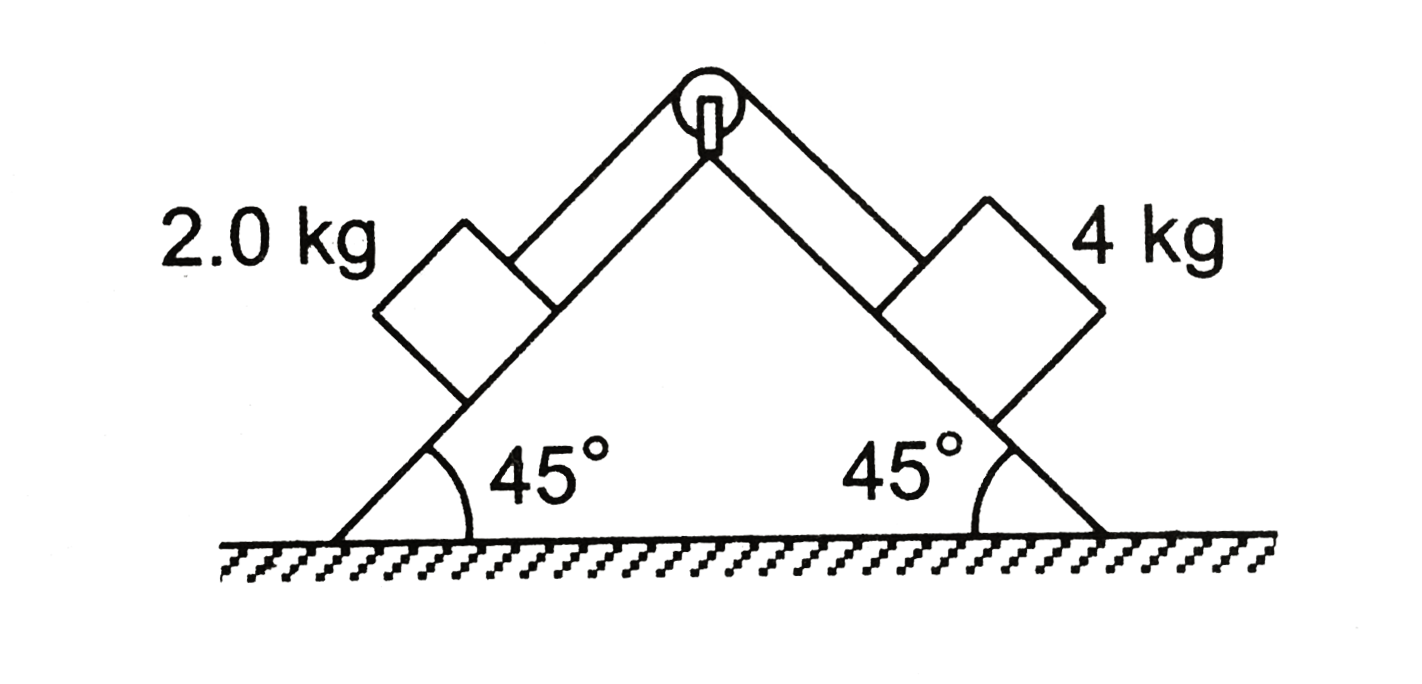
The pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
The correct Answer is:B
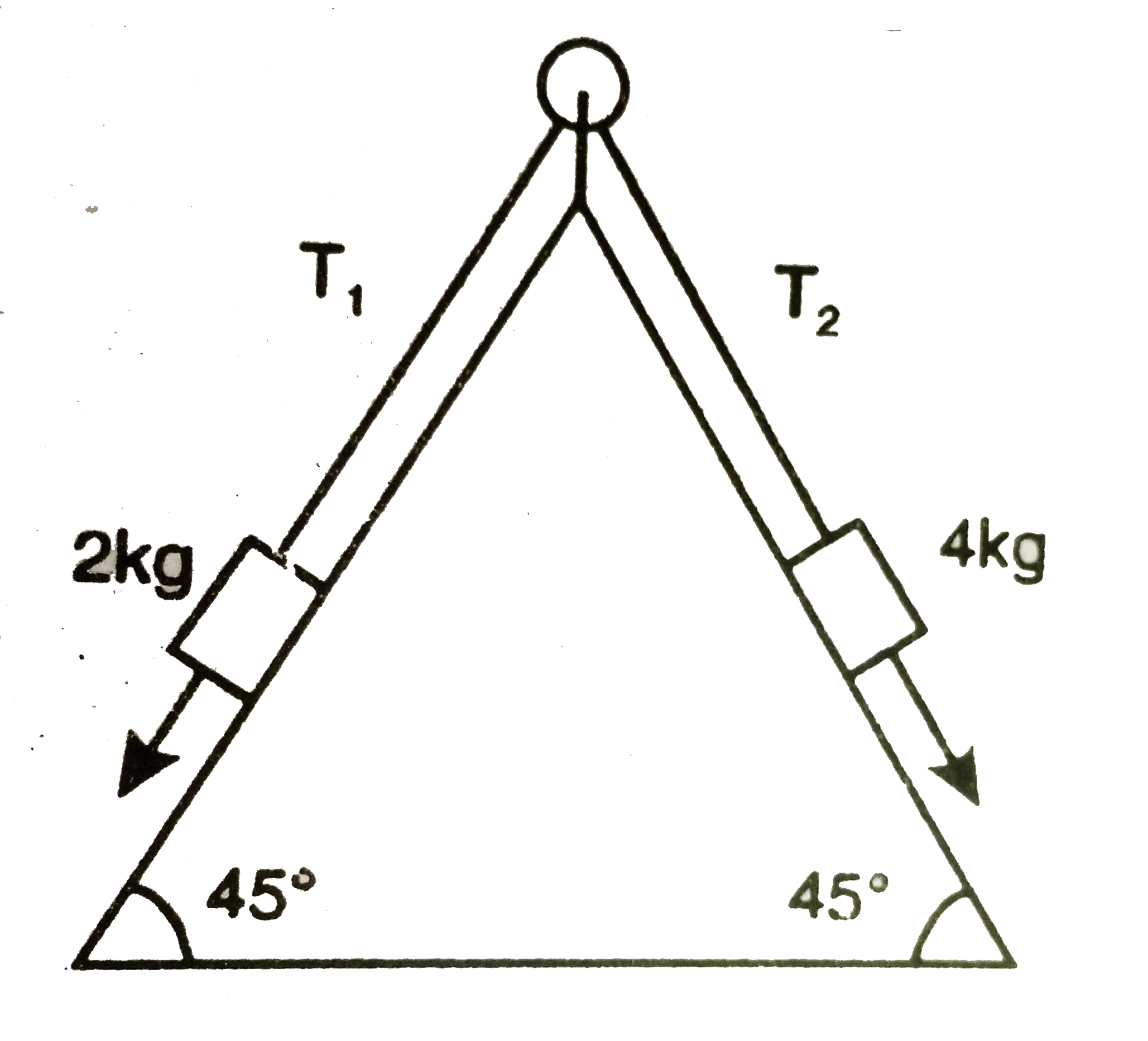
…….1
…..2
…….3
Adding the equation 1 and 3 we will get
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
The descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m^2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.

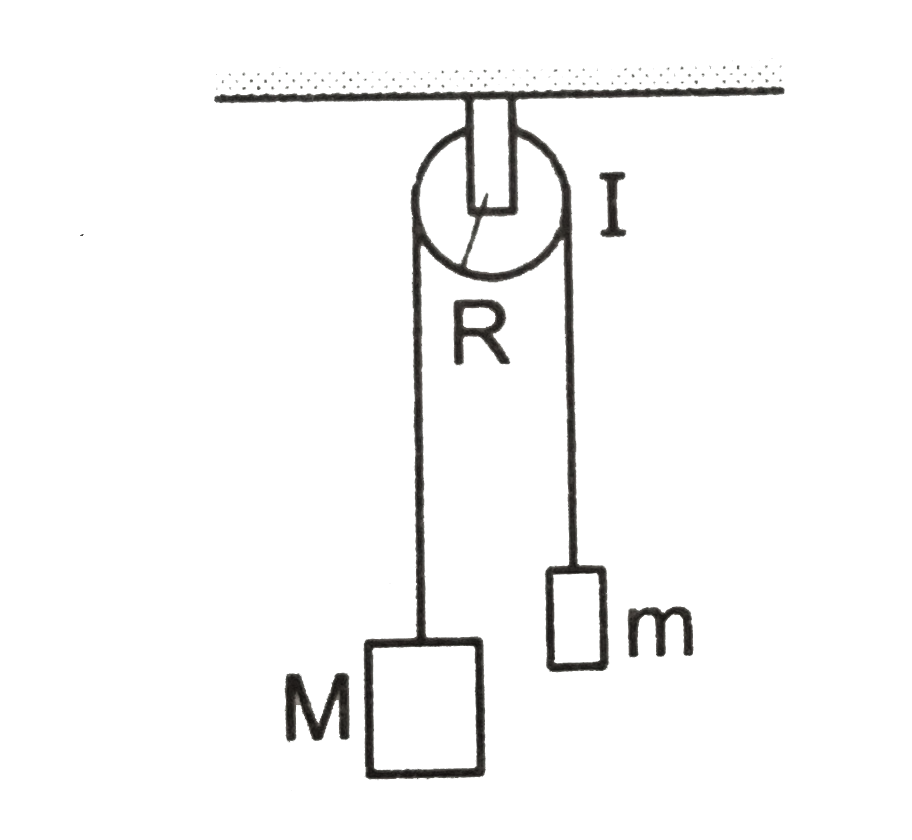
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View Solution
Knowledge Check
The rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
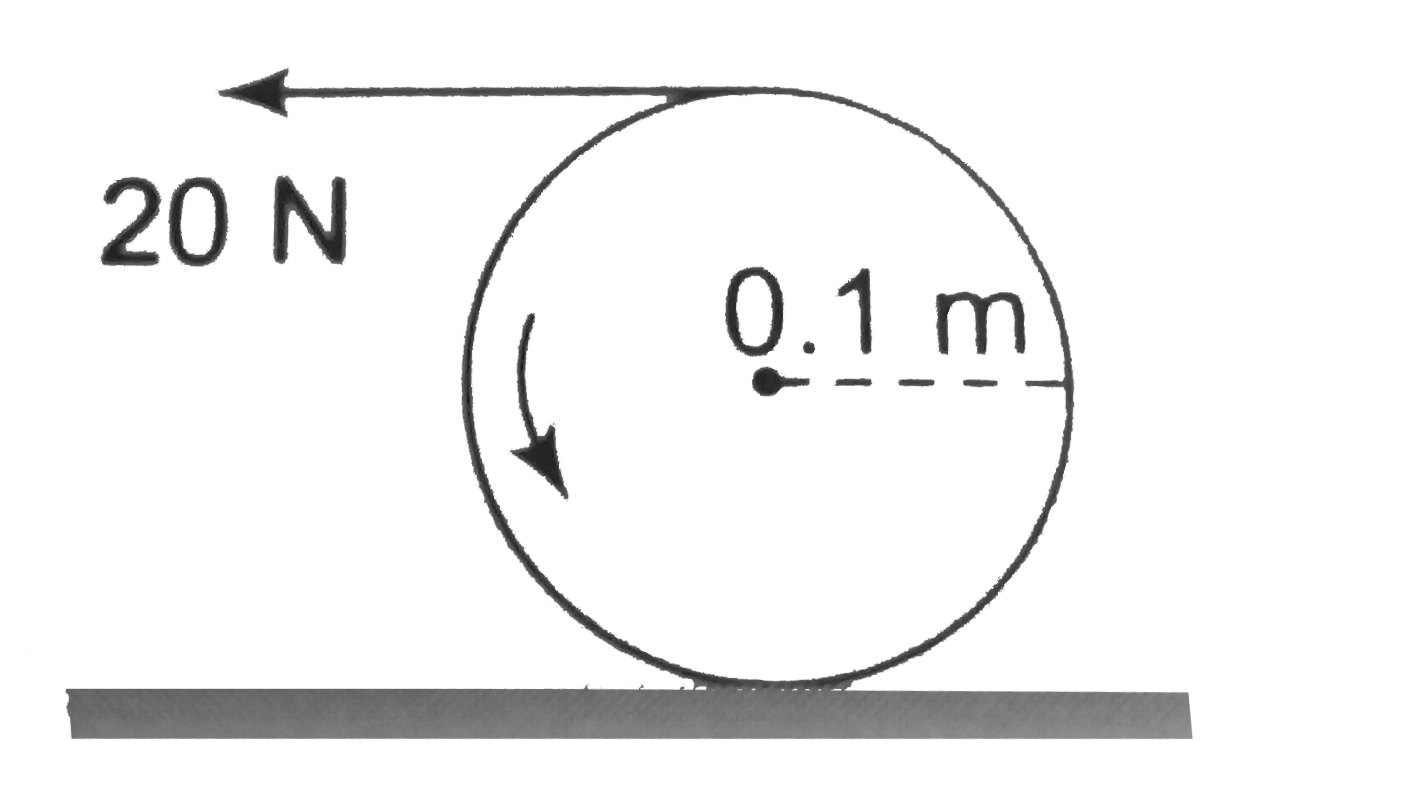 .A6.7m/s2B10.0m/s2C3.3m/s2Dnone of these
.A6.7m/s2B10.0m/s2C3.3m/s2Dnone of theseA wheel of mass 10 kg has a moment of inertia of 160kg−m2 about its own axis, the radius of gyration will be
A10mB8mC6mD4mA wheel of mass 15 kg has a moment of inertia of 200 kg m2 about its own axis, the radius of gyration will be
A3.6mB4mC4.6mD1.21m
Suppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m^2. Find the tension in the part of the string joiningk the pulleys.
View SolutionTwo blocks 4 kg and 2 kg are sliding down an incline plane as shown in figure. The acceleration of 2 kg block is.

View SolutionA thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… .
View Solution
A small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will be
View SolutionA fixed pulley of radius 20 cm and moment of inertia 0.32 kg.m2 about its axle has a massless cord wrapped around its rim. A mass M of 2 kg is attached to the end of the cord. The pulley can rotate about its axis without any friction. The acceleration of the mass M is :- (Assuming g=10m/s2)

View Solution
