The radii of spherical capacitor electrodes are equal to a and b, with a<b. The interlectordes ε and resistivity ρ. Inititally the capacitor is not charged. At the moment t=0 the internal electorde gets a charge q0 Find:
(a) the times variation of the charge on the internal elecrtordes,
(b) the amount of the heat generated during the spreading of the charge.
(a) Let us mentally isolatate a thin spherical layer with inner and outer radii r and r+dr respective. Lince of current at all the points of this layer are perpendicular to it and therefore such a layer can be treated as a spherical conductor of thickness dr and cross sectional area 4πr3. Now we know that resistance,
dR=ρdrS(r)=ρdr4πr2 ....(1)
Intergating expression (1) between teh Hints,
∫R0dR=∫bRρdr4πr2 or, R=ρ4π[1a−1b] ......(2)
Capacitance of the network, C=4πε0ε[1a−1b] ......(3)
and q=Cφ [where q is the charge at any arbitary moment] ....(4)
also, φ=(−dqdt)Ras capacitor is discharging, ....(5)
From Eqs.(2), (3),(4) and (5) we get,
q=4πε0ε[1a−1b][−dqdt]ρ[1a−1b]4π or, dqq=dtρεε0
Intergating ∫qq0−dqq=1ρε0ε∫t0dt=dtρεε0
Hence q=q0e−tρε0ε
(b) From energy conservation heat generated,m during the spreading of the charge,
H=Ui−Uf [because Acell=0]
=12q204πε0ε[1a−1b]−0=q208πε0εonb−aab
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
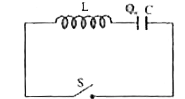 Aπ√LCB32π√LCCπ2√LCD2π√LC
Aπ√LCB32π√LCCπ2√LCD2π√LC - Question 2 - Select One
A capacitor of 4μF is connected as shwon in the figure. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
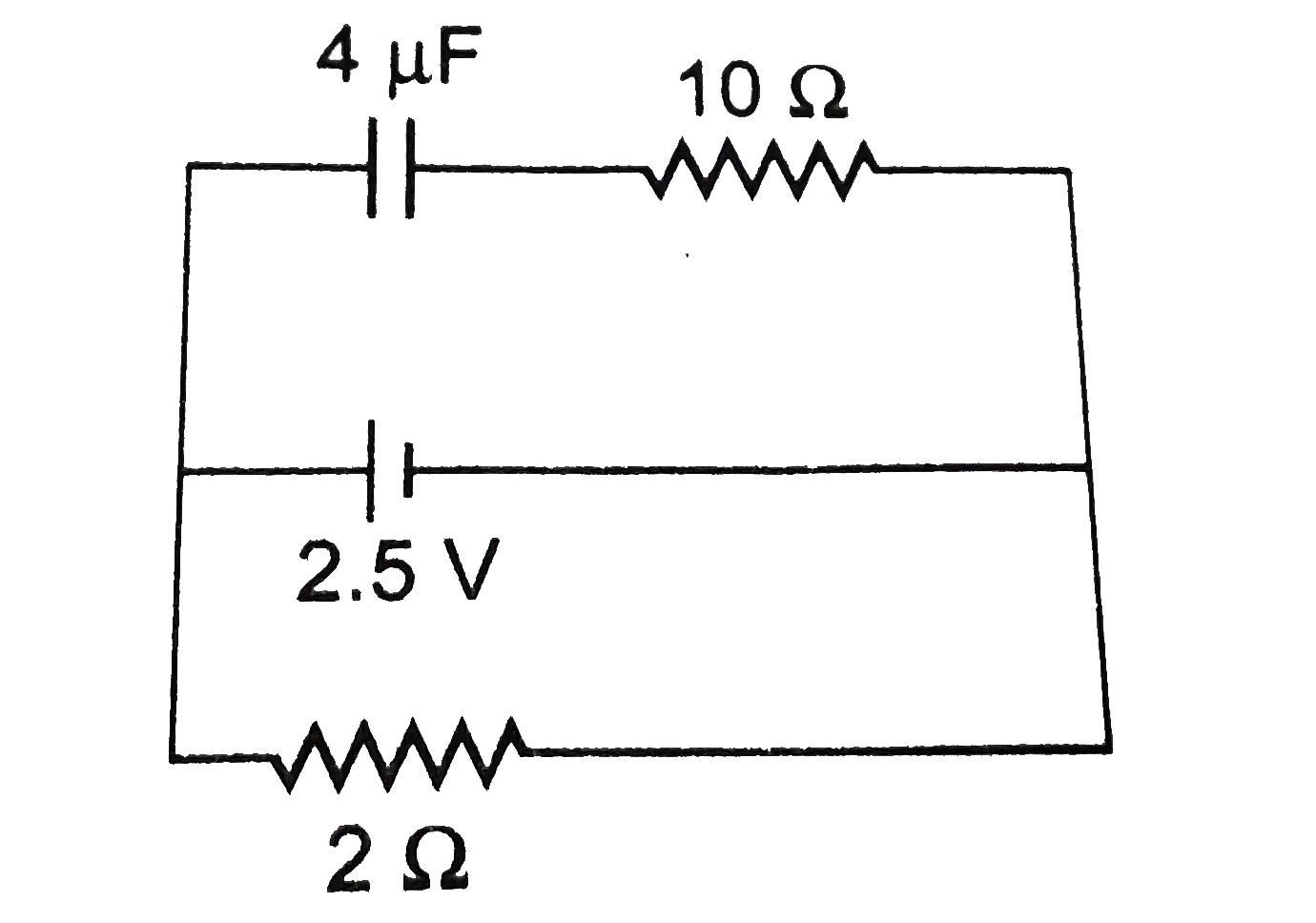 A0B4μCC16μCD8μC
A0B4μCC16μCD8μC - Question 3 - Select One
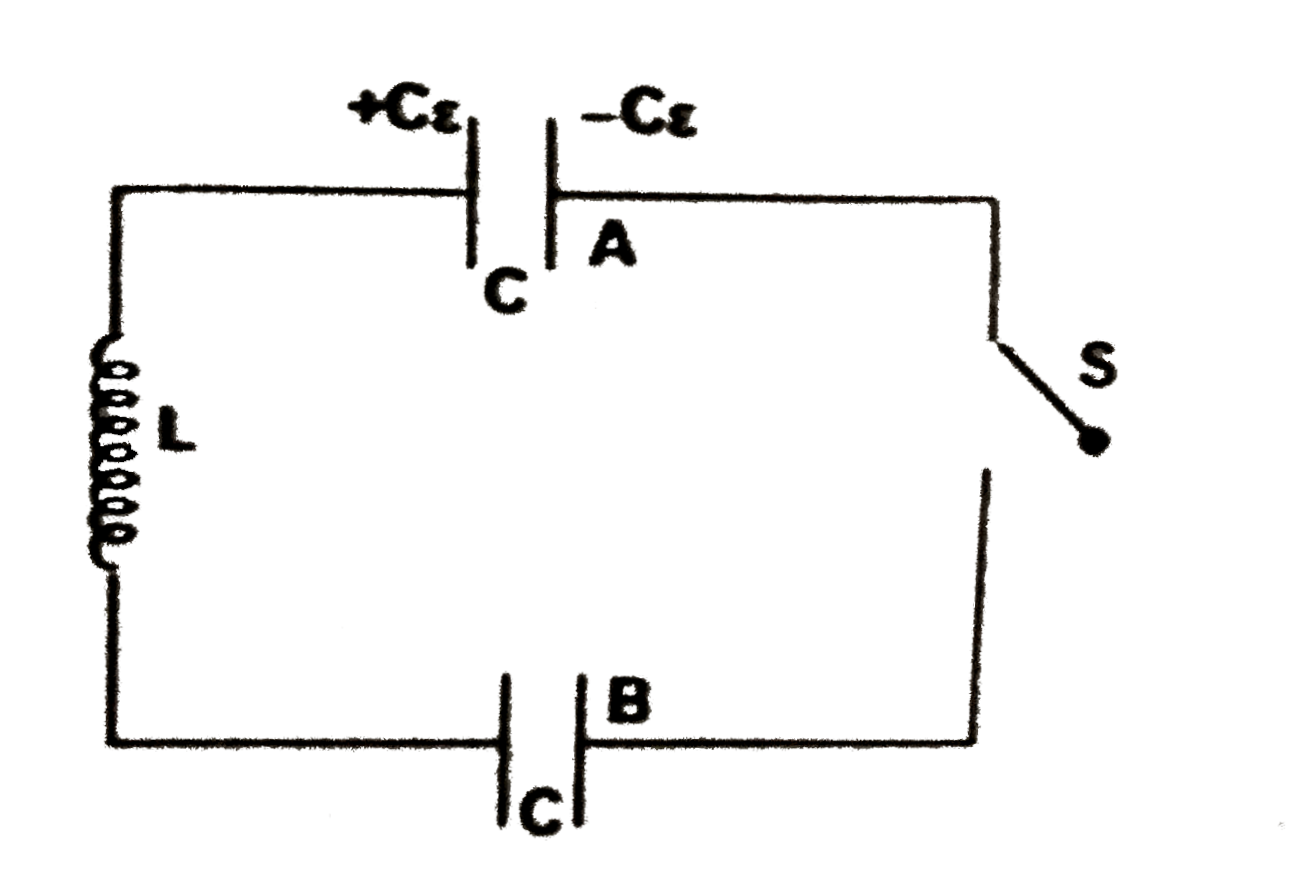
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor isAε√C2LBε√CLC2ε(CL)Dε2√CL
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.
 View Solution
View Solution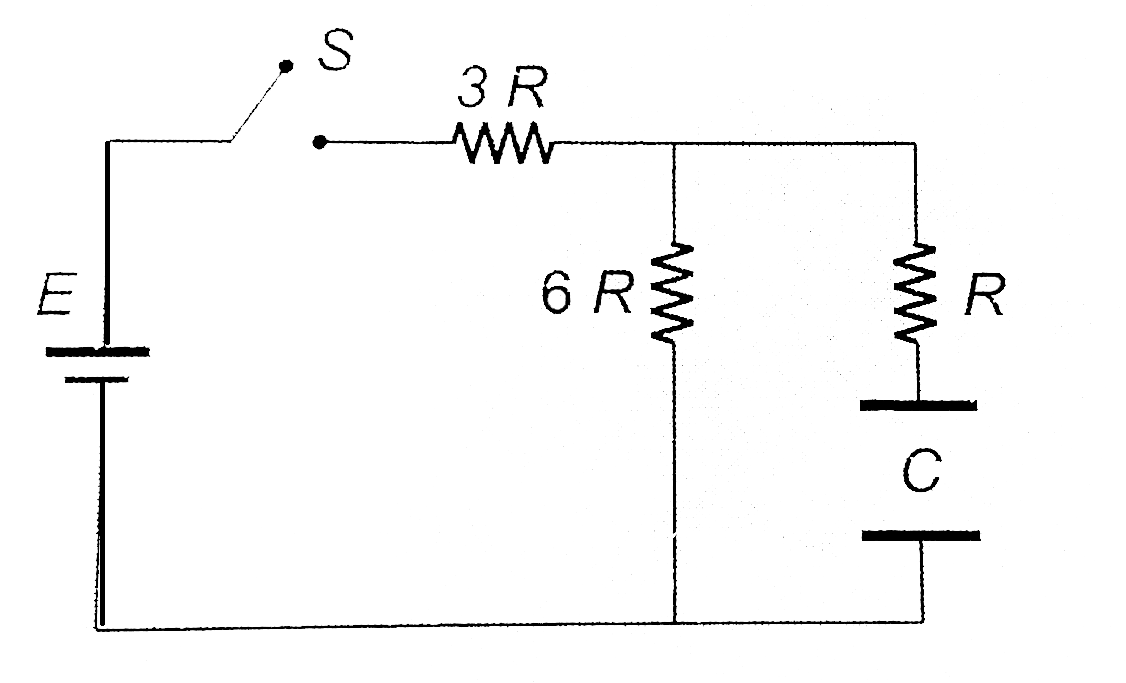
Find (a) equivalent time constant, (b) charge on capacitor in terms of time t.View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
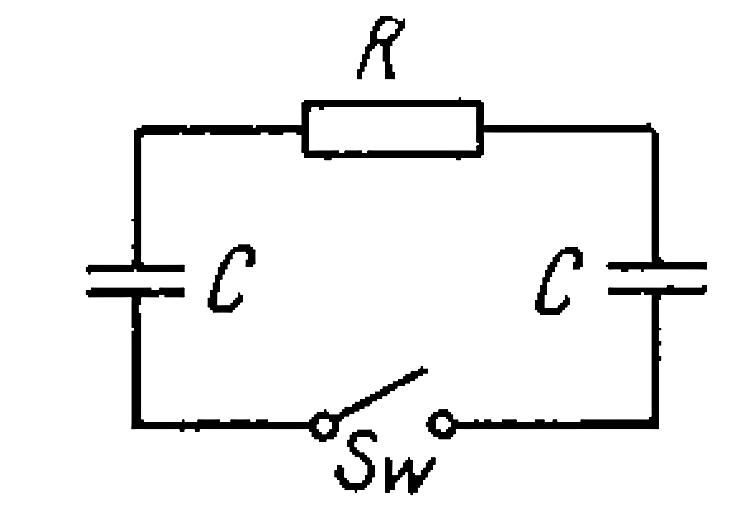
View SolutionIn a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
 View Solution
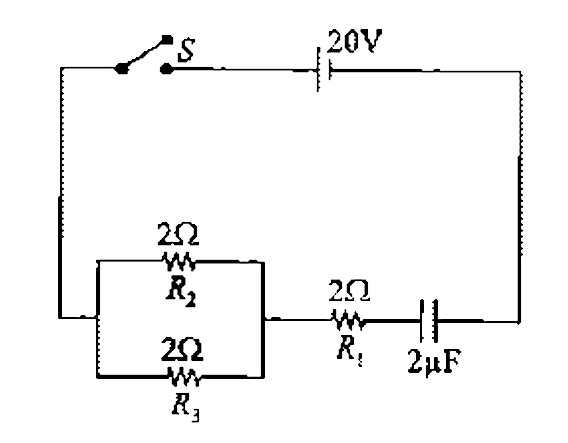
View SolutionThe circuit shown in figure-3.343 is closed at t=0. Calculate the total amount of heat generated in R2 during the time capacitor gets fully charged :
 View Solution
View Solution