The radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
15 cm
20 cm
5 cm
10 cm
The correct Answer is:D
To find the focal length of a plano-convex lens when the plano surface is silvered, we can follow these steps:
Step 1: Identify the parameters
- Radius of curvature (R) of the curved surface = 10 cm
- Refractive index (n) of the lens = 1.5
Step 2: Use the lens maker's formula
The lens maker's formula for a thin lens is given by:
1f=(n−1)(1R1−1R2)
Where:
- f = focal length of the lens
- n = refractive index of the lens
- R1 = radius of curvature of the first surface (convex surface)
- R2 = radius of curvature of the second surface (plane surface)
For a plano-convex lens:
- R1=10 cm (convex surface)
- R2=∞ (plane surface)
Step 3: Substitute the values into the formula
Substituting the values into the lens maker's formula:
1f=(1.5−1)(110−1∞)
1f=0.5(110−0)
1f=0.5×110=0.510=120
Step 4: Calculate the focal length
Taking the reciprocal to find f:
f=20 cm
Step 5: Consider the silvering of the plano surface
When the plano surface is silvered, the effective focal length of the system changes. The new effective focal length f′ after silvering is given by:
f′=f2
Substituting the previously calculated focal length:
f′=20 cm2=10 cm
Final Answer
The focal length of the lens after silvering the plano surface is 10 cm.
---
- Radius of curvature (R) of the curved surface = 10 cm
- Refractive index (n) of the lens = 1.5
The lens maker's formula for a thin lens is given by:
1f=(n−1)(1R1−1R2)
Where:
- f = focal length of the lens
- n = refractive index of the lens
- R1 = radius of curvature of the first surface (convex surface)
- R2 = radius of curvature of the second surface (plane surface)
- R1=10 cm (convex surface)
- R2=∞ (plane surface)
Substituting the values into the lens maker's formula:
1f=(1.5−1)(110−1∞)
1f=0.5(110−0)
1f=0.5×110=0.510=120
Taking the reciprocal to find f:
f=20 cm
When the plano surface is silvered, the effective focal length of the system changes. The new effective focal length f′ after silvering is given by:
f′=f2
Substituting the previously calculated focal length:
f′=20 cm2=10 cm
The focal length of the lens after silvering the plano surface is 10 cm.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Competition)Comprehension
Explore 7 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Integer Question
Explore 4 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Exemplar) Multiple choice
Explore 16 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View Solution
Knowledge Check
The radius of curvature of the face of plano-convex lens is 12cm and its refractive index is 1.5. If the plane surface of the lens is now silvered, then find the focal length of the lens.
A26cmB22cmC24cmD2cmThe radius of curvature of a thin planoconvex lens is 10 cm and the refractive index of its glass is 1.5. If the plane surface is silvered, then it will behave like a
Aconcave mirror of focal length 10 cmBconcave mirror of focal length 20 cmCconvex mirror of focal length 10 cmDconvex mirror offocal length 20 cmThe radius of curvature of the convex surface of a thin plano-convex lens is 15 cm and the refractive index of its material is 1.6. The power of the lens is
A+1DB−2DC+3DD+4D
The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionThe radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
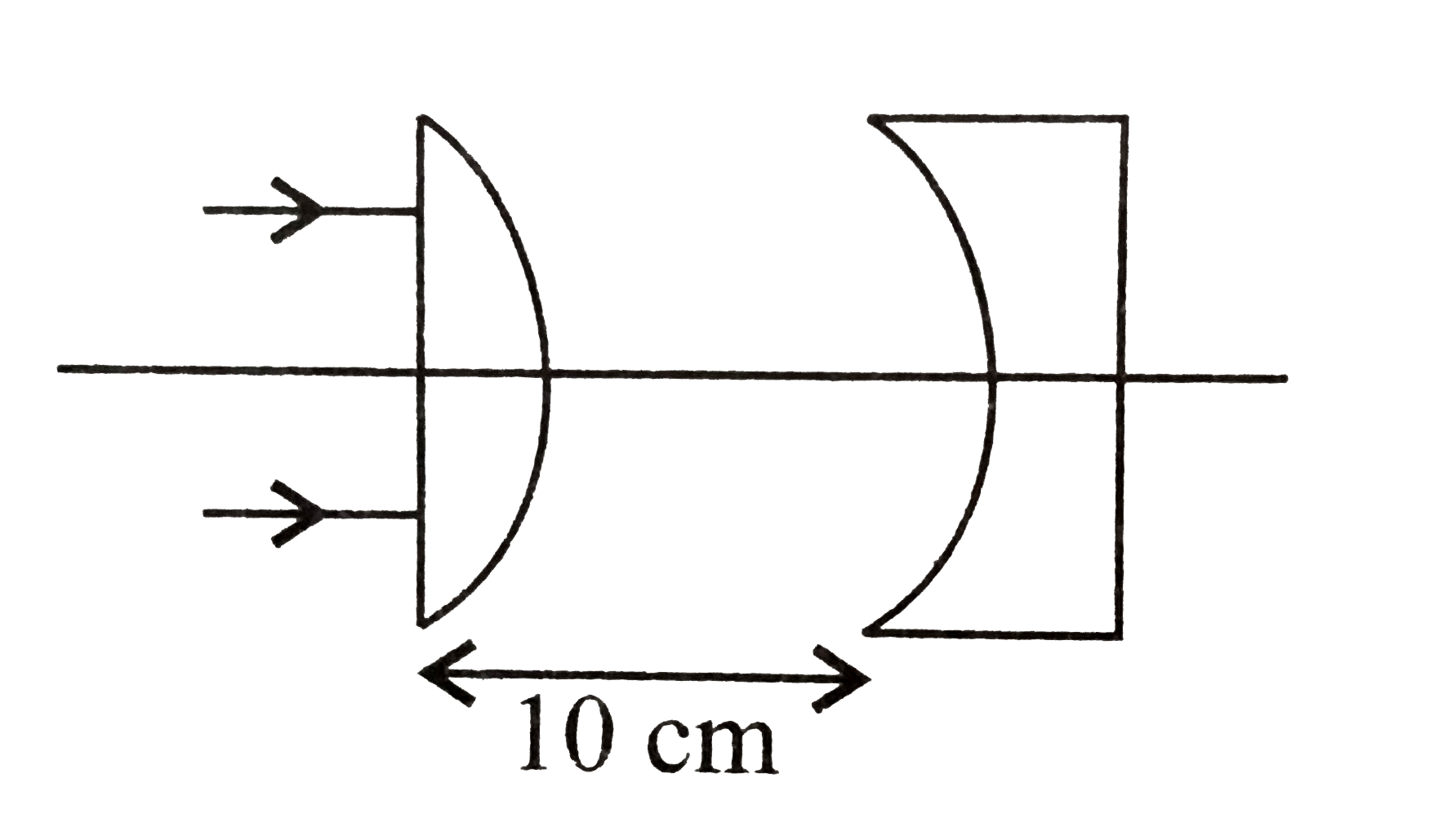
View SolutionIn the given figure, the radius of curvature of curved surface for both the plano-convex and plano-concave lens is 10 cm and refractive index for both is 1.5. The location of the final image after all the refractions through lenses is
View SolutionIf in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View SolutionThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
View Solution