The relation between the acceleration a and displacement x of a particle executing SHM is a=−(p/q)y , where p and q are constant quantities. What will be the time period of oscillation of the particle ? If p is doubled and q is halved, then find the value of new time period of oscillation.
To solve the problem, we will follow these steps:
Step 1: Understand the given relation
The relation provided is:
a=−pqy
where a is the acceleration, y is the displacement, and p and q are constants.
Step 2: Relate the given equation to SHM
In simple harmonic motion (SHM), the acceleration a can also be expressed as:
a=−ω2y
where ω is the angular frequency.
Step 3: Equate the two expressions for acceleration
From the two expressions for acceleration, we have:
−pqy=−ω2y
By canceling y (assuming y≠0), we get:
pq=ω2
Step 4: Find the angular frequency ω
From the equation pq=ω2, we can express ω as:
ω=√pq
Step 5: Calculate the time period T
The time period T of oscillation is related to the angular frequency ω by the formula:
T=2πω
Substituting for ω:
T=2π√pq=2π√qp
Step 6: Determine the new time period when p is doubled and q is halved
If p is doubled, we have p′=2p, and if q is halved, we have q′=q2.
Step 7: Calculate the new angular frequency ω′
Using the new values:
ω′=√p′q′=
⎷2pq2=√2p⋅2q=√4pq=2√pq=2ω
Step 8: Calculate the new time period T′
Now, substituting ω′ into the time period formula:
T′=2πω′=2π2ω=2π2⋅√pq=12T
Final Answer
Thus, the new time period of oscillation when p is doubled and q is halved is:
T′=12T
The relation provided is:
a=−pqy
where a is the acceleration, y is the displacement, and p and q are constants.
In simple harmonic motion (SHM), the acceleration a can also be expressed as:
a=−ω2y
where ω is the angular frequency.
From the two expressions for acceleration, we have:
−pqy=−ω2y
By canceling y (assuming y≠0), we get:
pq=ω2
From the equation pq=ω2, we can express ω as:
ω=√pq
The time period T of oscillation is related to the angular frequency ω by the formula:
T=2πω
Substituting for ω:
T=2π√pq=2π√qp
If p is doubled, we have p′=2p, and if q is halved, we have q′=q2.
Using the new values:
ω′=√p′q′=
⎷2pq2=√2p⋅2q=√4pq=2√pq=2ω
Now, substituting ω′ into the time period formula:
T′=2πω′=2π2ω=2π2⋅√pq=12T
Thus, the new time period of oscillation when p is doubled and q is halved is:
T′=12T
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Long Answer Questions
Explore 33 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Advanced Problems For Competitions
Explore 20 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Very Short Answer Questions
Explore 99 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
The relation between the acceleration a and displacement x of a particle executing S.H.M. is a=−(p/q)y, where p and q are constants. What will be the time period T of the particle ?
View SolutionWrite the relation between time period T, displacement x and acceleration a of a particle in S.H.M.
View Solution
Knowledge Check
The time period of oscillation of a particle in S.H.M. depends
Anot upon its mass,Bupon its mass,Cupon amplitude of the S.H.M.Dupon phase of the particle.If p×q=p+q+pq, then find the value of 8×2.
A20B10C14D16The acceleration-displacement graph of two particles P and Q exeucting SHM are represented as shown in the figure. The ratio of time periods of P, q respectively is
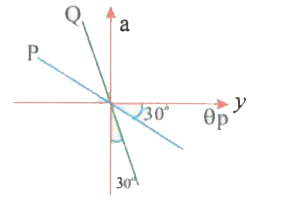 A√3:1B1:√3C3:1D1:3
A√3:1B1:√3C3:1D1:3
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionA particle executes SHM with a time period of 2 s and amplitude 5 cm. What will be the displacement and velocity of that particle at t = 1/3 ?
View SolutionThe displacement of a particle executing SHM at any time t (Seconds) is x=0.01sin100π(t=0.005) then its time period will be
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
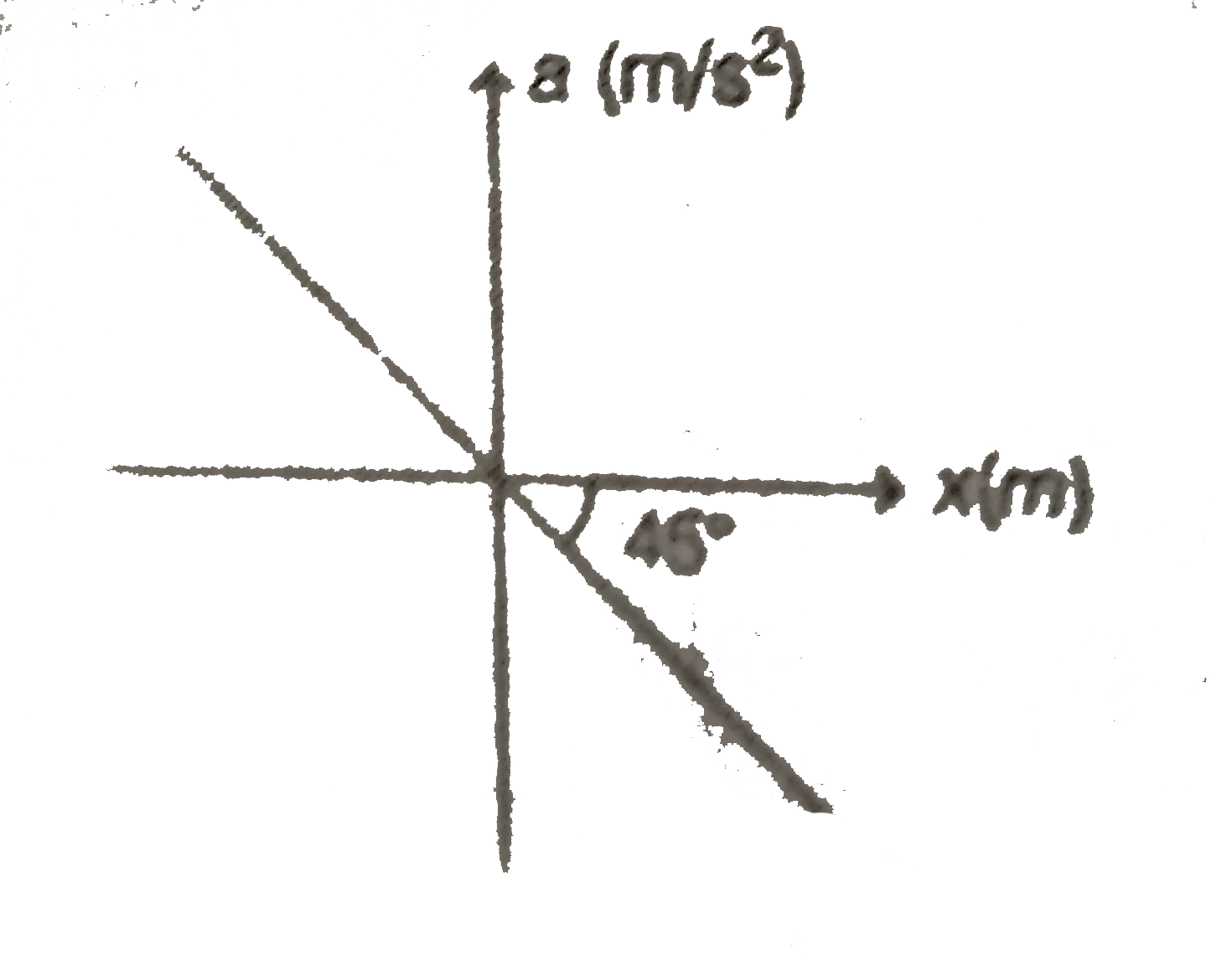
View Solution