The resistivity of a wire is ρ, its volume is 3m3 and resistance is 3Ω, then its length will be
3ρ
3√ρ
√3ρ
ρ√3
The correct Answer is:B
To find the length of the wire given its resistivity, volume, and resistance, we can follow these steps:
Step 1: Understand the relationship between resistance, resistivity, length, and area.
The resistance R of a wire can be expressed using the formula:
R=ρLA
where:
- R = resistance (in ohms)
- ρ = resistivity of the material (in ohm-meters)
- L = length of the wire (in meters)
- A = cross-sectional area of the wire (in square meters)
Step 2: Express the volume of the wire in terms of area and length.
The volume V of the wire can be expressed as:
V=A×L
Given that the volume of the wire is 3m3, we can write:
3=A×L
From this, we can express the area A in terms of length L:
A=3L
Step 3: Substitute the expression for area into the resistance formula.
Now, substitute A into the resistance formula:
R=ρL3L=ρL23
Given that the resistance R is 3Ω, we can set up the equation:
3=ρL23
Step 4: Solve for L2.
To isolate L2, multiply both sides by 3:
9=ρL2
Now, rearranging gives:
L2=9ρ
Step 5: Solve for L.
Taking the square root of both sides, we find:
L=√9ρ=3√ρ
Final Answer:
Thus, the length of the wire L is:
L=3√ρ
---
The resistance R of a wire can be expressed using the formula:
R=ρLA
where:
- R = resistance (in ohms)
- ρ = resistivity of the material (in ohm-meters)
- L = length of the wire (in meters)
- A = cross-sectional area of the wire (in square meters)
The volume V of the wire can be expressed as:
V=A×L
Given that the volume of the wire is 3m3, we can write:
3=A×L
From this, we can express the area A in terms of length L:
A=3L
Now, substitute A into the resistance formula:
R=ρL3L=ρL23
Given that the resistance R is 3Ω, we can set up the equation:
3=ρL23
To isolate L2, multiply both sides by 3:
9=ρL2
Now, rearranging gives:
L2=9ρ
Taking the square root of both sides, we find:
L=√9ρ=3√ρ
Thus, the length of the wire L is:
L=3√ρ
Topper's Solved these Questions
Similar Questions
Knowledge Check
The specific resistance of a wire is ρ, its volume is 3m3 and its resistance is 3ohms, then its length will be
A√1ρB3√ρC1ρ√3Dρ√13The specific resistance of a wire is ρ, its volume is 3m3 and its resistance is 3ohms, then its length will be
A√1/ρB3/√ρC√3/ρDρ/√3Resistivity of a material of wire is 3⋅10−6Ω−m and resistance of a particular thickness and length of wire is 2Ω. If the diameter of the wire gets doubled then the resistivity will be
A1.1⋅10−2Ω−mB1.5⋅10−3Ω−mC2⋅10−6Ω−mD3⋅10−6Ω−m
A length of copper wire carries a current of 3.5 A uniformly distributed through its cross section. Calculate the energy density of (a) the magnetic field and (b) the electric field at the surface of the wire. The wire diameter is 2.5 mm, and its resistance per unit length is 3.3 Ω/km.
View SolutionThe temperature co-effcient of resistance of a wire is 0.00125∘C. At 500 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at
View SolutionA wire of resistance x ohm is draw out, so that its length in increased to twice its original length, and its new resistance becomes 20 Ω then x will be .
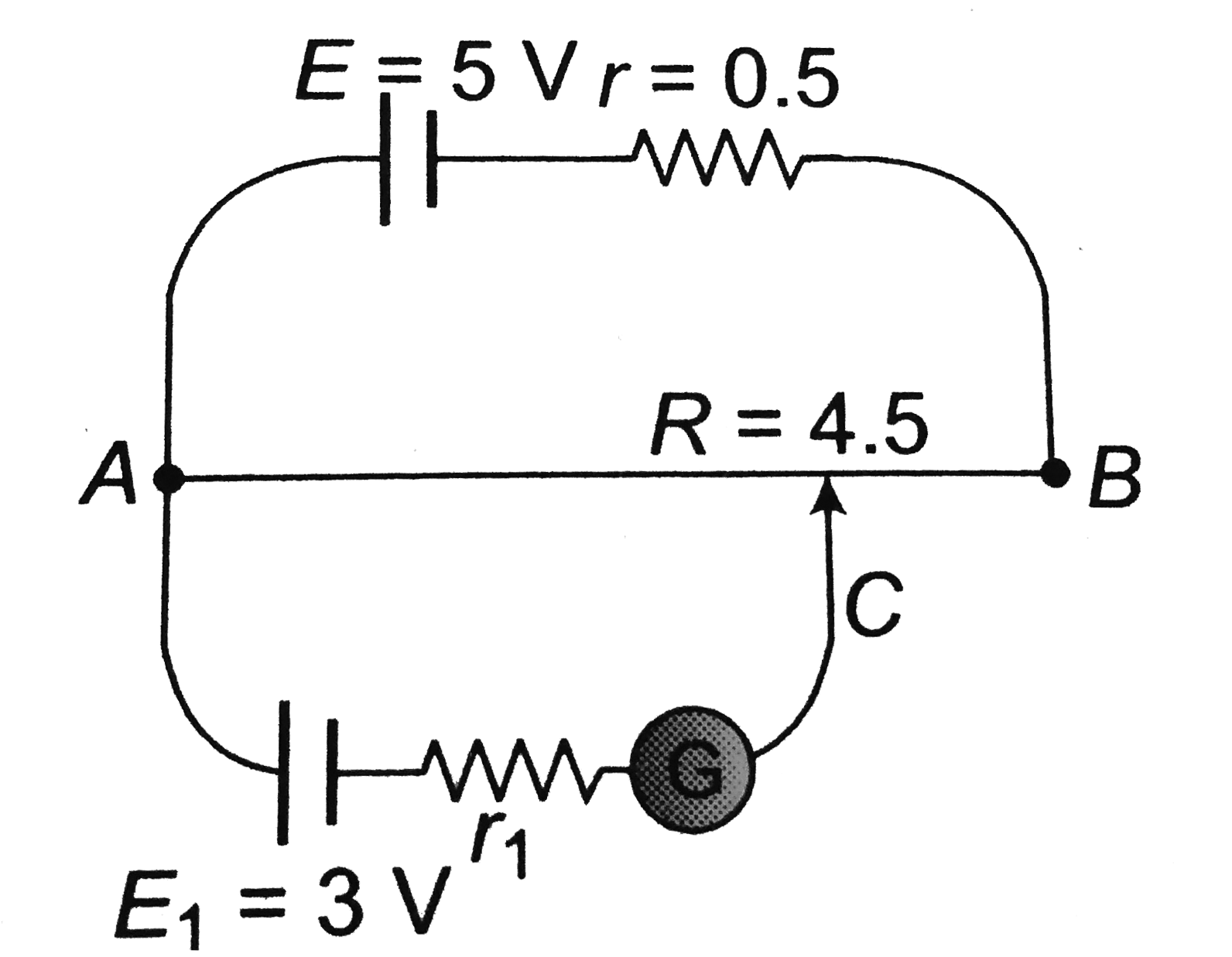
View SolutionIn the given potentiometer circuit length of the wire AB is 3m and resistance is R=4.5Ω. The length AC for no deflection in galvanometer is
View SolutionThe resistivity of a wire at 20∘C and 100∘C is 3Ω−m and 4Ω−m respectively. The resistivity of the wire at 0∘C is
View Solution
