The resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
P2−Q2PQ
P+QP−Q
Q
PQ
The correct Answer is:C
Step by step video & image solution for The resultant of two vectors vec(P) and vec(Q) is vec(R). If vec(Q) is doubled then the new resultant vector is perpendicular to vec(P). Then magnitude of vec(R) is :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-2 (Lami.s theorem :)
8 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-2 ( Relative velocity)
15 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Circular motion)
12 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
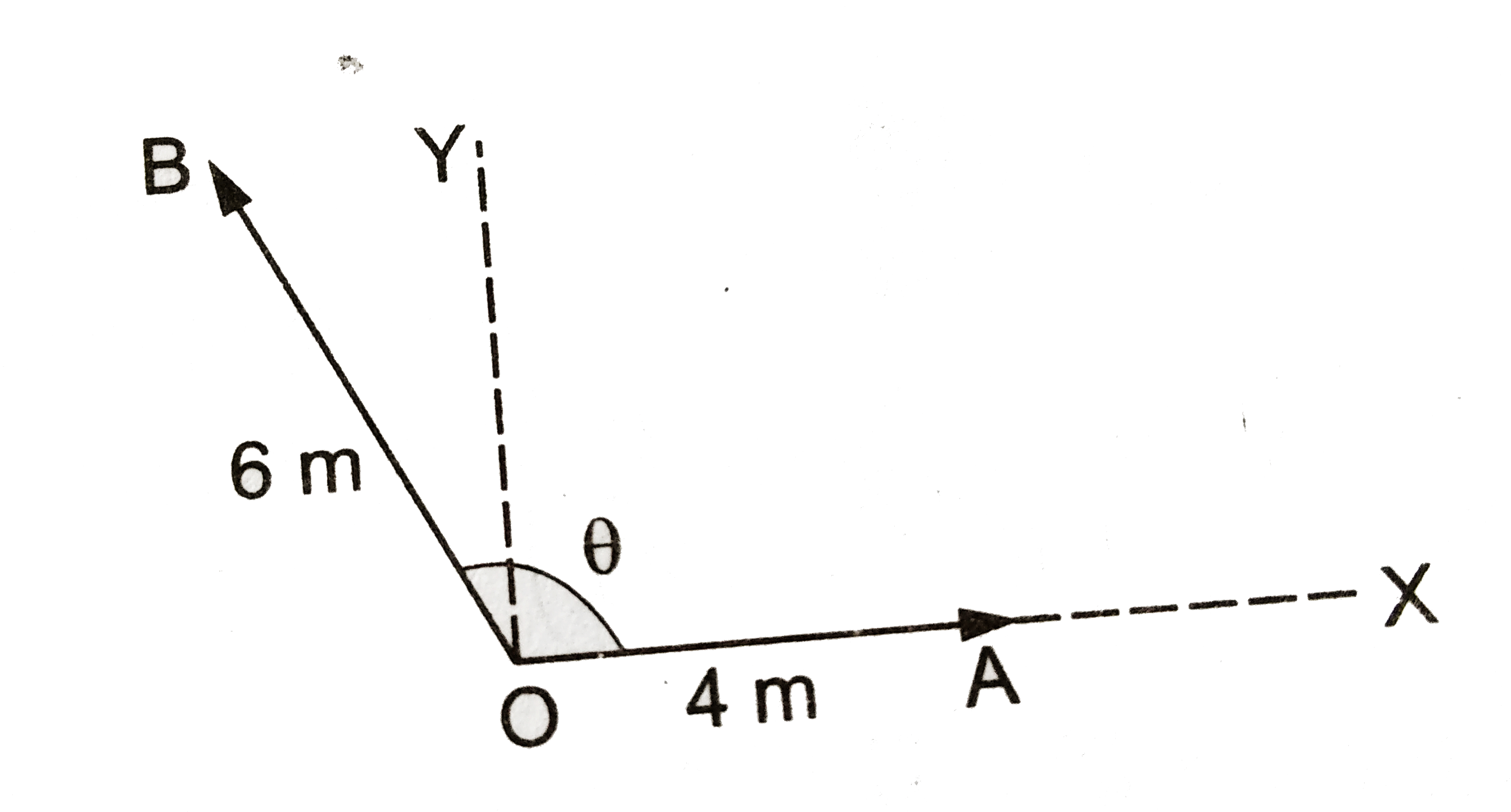
The resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
View SolutionThe resultant of →P and →Q is →R. If →Q is doubled, →R is doubled, when →Q is reversed, →R is again doubled. Find P:Q:R.
View SolutionThe resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionIf →aand→b are two vector such that ∣∣→a+→b∣∣=|→a|, then show that vector |2a+b| is perpendicular to →b.
View SolutionThe resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
View SolutionThe resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?
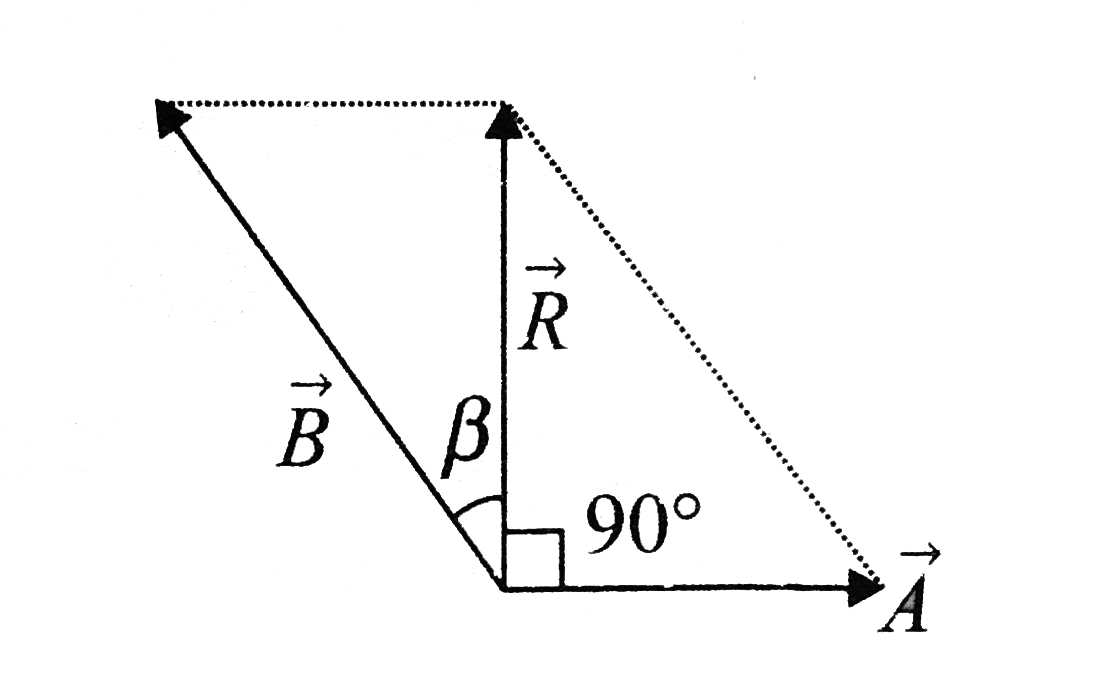
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ , find the angle between →P and →Q.
View SolutionIf →a,→b are two vectors such that ∣∣→a+→b∣∣=∣∣→b∣∣, then prove that →a+2→b is perpendicular to →a .
View SolutionIf two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
View Solution
