The resultant resistance of two resistance in series is 50 Ω and it is 12 Ω , when they are in parallel. The individual resistances are
20Ωand15Ω
15Ωand30Ω
20Ωand30Ω
10Ωand15Ω
The correct Answer is:C
To find the individual resistances R1 and R2 given that their resultant resistance in series is 50 ohms and in parallel is 12 ohms, we can follow these steps:
Step 1: Set up the equations
For resistors in series, the total resistance Rs is given by:
Rs=R1+R2
Given that Rs=50Ω, we have:
R1+R2=50(1)
For resistors in parallel, the total resistance Rp is given by:
Rp=R1×R2R1+R2
Given that Rp=12Ω, we can substitute R1+R2 from equation (1):
12=R1×R250(2)
Step 2: Rearranging equation (2)
From equation (2), we can rearrange it to find R1×R2:
R1×R2=12×50=600(3)
Step 3: Solve the system of equations
Now we have two equations:
1. R1+R2=50
2. R1×R2=600
We can express R1 in terms of R2 from equation (1):
R1=50−R2(4)
Substituting equation (4) into equation (3):
(50−R2)×R2=600
Expanding this gives:
50R2−R22=600
Rearranging leads to:
R22−50R2+600=0(5)
Step 4: Solve the quadratic equation
Using the quadratic formula R2=−b±√b2−4ac2a where a=1,b=−50,c=600:
R2=50±√(−50)2−4×1×6002×1
Calculating the discriminant:
R2=50±√2500−24002
R2=50±√1002
R2=50±102
This gives us two possible values for R2:
R2=602=30orR2=402=20
Step 5: Find corresponding R1
Using equation (4) to find R1:
1. If R2=30:
R1=50−30=20
2. If R2=20:
R1=50−20=30
Thus, the individual resistances are:
R1=30Ω,R2=20Ωor vice versa.
Final Answer:
The individual resistances are R1=30Ω and R2=20Ω.
---
For resistors in series, the total resistance Rs is given by:
Rs=R1+R2
Given that Rs=50Ω, we have:
R1+R2=50(1)
Rp=R1×R2R1+R2
Given that Rp=12Ω, we can substitute R1+R2 from equation (1):
12=R1×R250(2)
From equation (2), we can rearrange it to find R1×R2:
R1×R2=12×50=600(3)
Now we have two equations:
1. R1+R2=50
2. R1×R2=600
R1=50−R2(4)
(50−R2)×R2=600
Expanding this gives:
50R2−R22=600
Rearranging leads to:
R22−50R2+600=0(5)
Using the quadratic formula R2=−b±√b2−4ac2a where a=1,b=−50,c=600:
R2=50±√(−50)2−4×1×6002×1
Calculating the discriminant:
R2=50±√2500−24002
R2=50±√1002
R2=50±102
This gives us two possible values for R2:
R2=602=30orR2=402=20
Using equation (4) to find R1:
1. If R2=30:
R1=50−30=20
2. If R2=20:
R1=50−20=30
R1=30Ω,R2=20Ωor vice versa.
The individual resistances are R1=30Ω and R2=20Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Straight Objective Type Questions))
Explore 11 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))
Explore 3 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PROBLEMS (LEVEL-II)
Explore 27 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
Similar Questions
The equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View Solution(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent
resistance of a group of resistances joined in parallel is equal to the sum of the
reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12Ω each are joined in parallel to a 6V battery.
Find the current drawn from the battery.
View Solution
Knowledge Check
A microammeter has as resistance of 100Ω and full scale range of 50μA. It can be used a voltmeter or as ahigher range ammeter provided a resistance is added to it. Pick the correct range and resistance combinations
50 V range with 10kΩ resistance in series
b.10V range with 200kΩ resistance in series
c. 5mA rangw with 1Ω resistance in parallel
10mA range with 1Ω resistance in parallelA50 V range with 10kΩ resistance in seriesB10 V range with 200kΩ resistance in series.C5mA range with 2Ω resistance in parallelD10 mA range with 2Ω resistance in parallel
The Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionA battery supplies 150W and 196 W power to two resistance of 6Ω and 4Ω when they are connected separately to it. The internal resistance of the battery is:-
View SolutionA uniform wire with a resistance of 27 Ω is divided into three equal pieces and then they are joined in parallel. Find the equivalent resistance of the parallel combination
View SolutionA microammeter has as resistance of 100Ω and full scale range of 50μA. It can be used a voltmeter or as ahigher range ammeter provided a resistance is added to it. Pick the correct range and resistance combinations
50 V range with 10kΩ resistance in series
b.10V range with 200kΩ resistance in series
c. 5mA rangw with 1Ω resistance in parallel
10mA range with 1Ω resistance in parallel
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
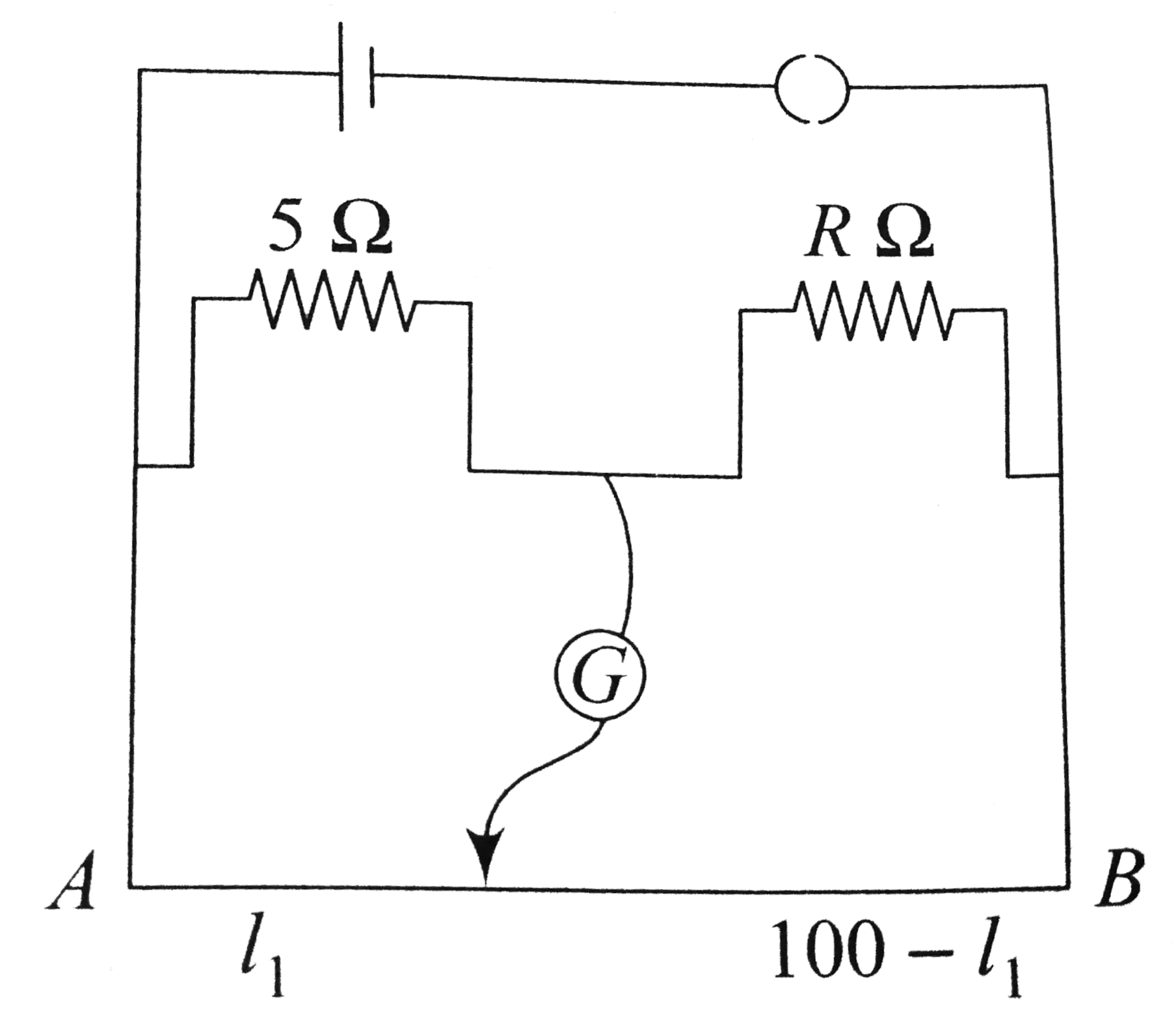
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

View Solution