(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent
resistance of a group of resistances joined in parallel is equal to the sum of the
reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12Ω each are joined in parallel to a 6V battery.
Find the current drawn from the battery.
Solution:
(a) To prove that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances, we will consider a circuit with three resistors R1,R2, and R3 connected in parallel.
1. Circuit Diagram: Draw a circuit diagram with a battery and three resistors in parallel. Label the resistors R1,R2, and R3 and connect them between the two terminals of the battery.
2. Current Division: Let the total current flowing from the battery be I. This current divides into three parts:
- I1 through R1
- I2 through R2
- I3 through R3
Thus, we can write:
I=I1+I2+I3
3. Voltage Across Resistors: Since the resistors are in parallel, the voltage across each resistor is the same and equal to the voltage of the battery V:
V=V1=V2=V3
4. Ohm's Law: According to Ohm's Law, we can express the currents through each resistor as:
I1=VR1,I2=VR2,I3=VR3
5. Substituting Currents: Substitute I1,I2, and I3 back into the equation for total current:
I=VR1+VR2+VR3
6. Factoring Out Voltage: Factor out V:
I=V(1R1+1R2+1R3)
7. Equivalent Resistance: The equivalent resistance Req can be defined as:
I=VReq
8. Equating Currents: Set the two expressions for I equal to each other:
VReq=V(1R1+1R2+1R3)
9. Cancelling Voltage: Since V is not zero, we can cancel it from both sides:
1Req=1R1+1R2+1R3
Thus, we have proved that the reciprocal of the equivalent resistance Req is equal to the sum of the reciprocals of the individual resistances.
---
(b) Now, let’s find the current drawn from the battery when two resistors of 12Ω each are connected in parallel to a 6V battery.
1. Identifying Resistors: We have two resistors R1=12Ω and R2=12Ω.
2. Finding Equivalent Resistance: Using the formula for resistors in parallel:
1Req=1R1+1R2
Substitute the values:
1Req=112+112=212=16
Therefore, the equivalent resistance is:
Req=6Ω
3. Applying Ohm's Law: Now, we can calculate the current I using Ohm's Law:
I=VReq=6V6Ω=1A
Thus, the current drawn from the battery is 1A.
---
- I1 through R1
- I2 through R2
- I3 through R3
I=I1+I2+I3
V=V1=V2=V3
I1=VR1,I2=VR2,I3=VR3
I=VR1+VR2+VR3
I=V(1R1+1R2+1R3)
I=VReq
VReq=V(1R1+1R2+1R3)
1Req=1R1+1R2+1R3
1Req=1R1+1R2
Substitute the values:
1Req=112+112=212=16
Therefore, the equivalent resistance is:
Req=6Ω
I=VReq=6V6Ω=1A
Similar Questions
A battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionIn the adjacent circuit diagram , each resister is of 16Ω . The equivalent resistance between A and B is
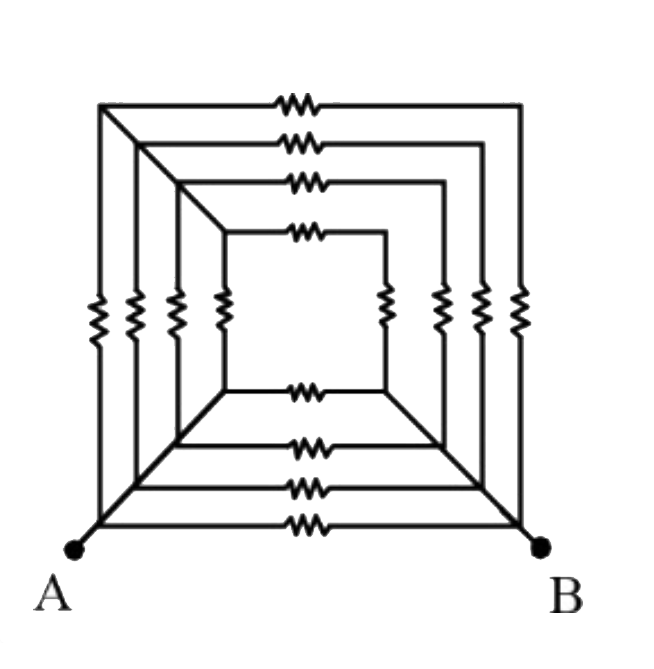
View SolutionIn the given electric circuit if the current flowing through 3Ω resistor is 1 A, find the voltage of the battery and the current I drawn from it.

View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View SolutionA wire of 20Ω resistance is gradually stretched to double its original length. It is then cut into two equal parts. These parts are then connected in parallel across a 4.0 volt battery. Find the current drawn from the battery.
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
View SolutionIn the circuit shown, if the 10Ω resistance is replaced by 20Ω Then the amount of current draw from the battery will be
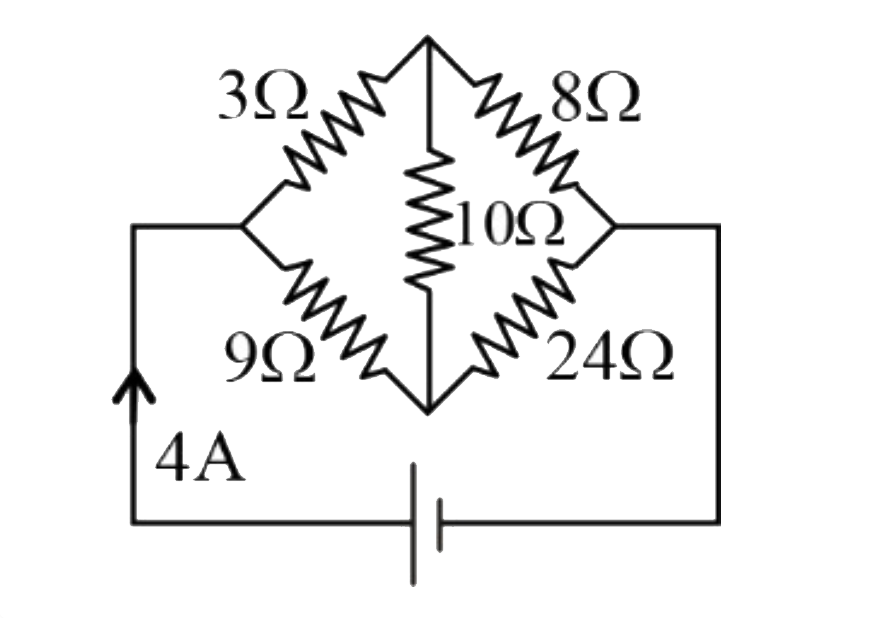
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View Solution
