The spring as shown in figure is kept in a stretched position with extension Xo when the system is released. Assuming the horizontal surface to be frictionless, the frequency of oscillation is
 Solution in Tamil
Solution in Tamil
Considerign the two blocks plus the spring as a system, there is o exterN/Al resultant force on the system. Hence the centre of mass of the system will remain at rest. tE mean positions of the two simple harmonic motions occur whe the spring becomes unstretched. If the mass m moves towasrds right through a distance x and the mass M moves towards left through a distance X before the spring acquires N/Atural lenght
x+X=x0.............i
x and X will be the amplitudes of the two blocks m and M respectively. As the centre of mass should not change during the motion, we should also have
mx=MX............ii ltbrogt From i and ii x=Mx0M+mandX=mx0M+m
Hence the left block is x=Mx0M+m distance away from its mean position in the beginning of the motion. the force by the spring on this block at this instant is equal to the tension of spring
T=kx0
Now x=Mx0M+mor,x0=M+mMx
Thus,T=k(M+m)Mxor,a=Tm=k(M+m)Mmx
Theanga––requencyis∴omega=(sqrt(k(M+m))/(Mm))<br>andtheequencyisv=omega/(2pi)=1/(2pi)(sqrt((M+m))/(Mm))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A person goes to bed at shasrp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no why?
View SolutionA student says that he had applied a force F=−k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View SolutionThe frequency of oscillation of the spring shown in the figure will be
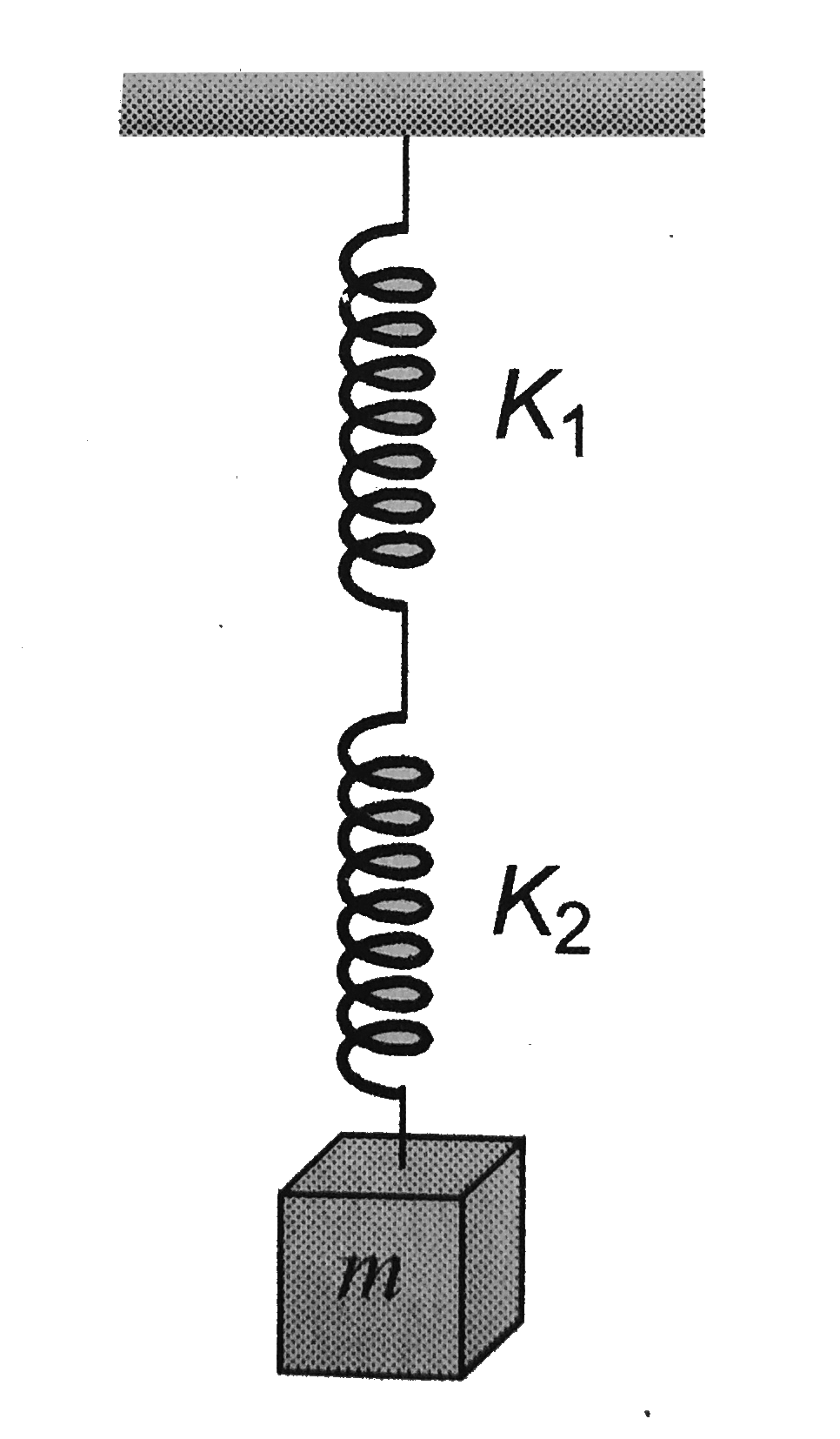
View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
View SolutionThe frequency of oscillation of the springs shown in the figure will be
View SolutionFour massless springs whose force constants are 2k,2k, k and 2k, respectively, are attached to a mass M kept on a frictionless plane (as shown in figure), If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is
View SolutionConsider the situations shown in fig (a) and (b) initially the spring is unstretched when the mass m is released from rest. Assuming no friction in the pulley find (a) the maximum stretch in the spring (b) stretch in the spring when the system is in equilibium.
View SolutionThe frequency of oscillation of the system shown in the figure will be
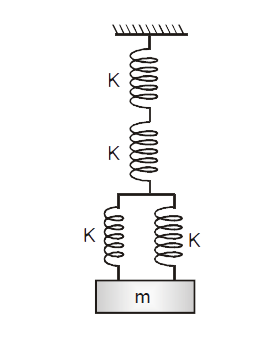
View SolutionIn the systems shown in figure (A), (B), (C) and (D), the scales of the springs are calibrated in newton Assume that Pulleys are massless and frictionless Strings are massless The surface in figure (D) is frictionless Reading of the spring scale in figure (A) is
View SolutionIn the systems shown in figure (A), (B), (C) and (D), the scales of the springs are calibrated in newton
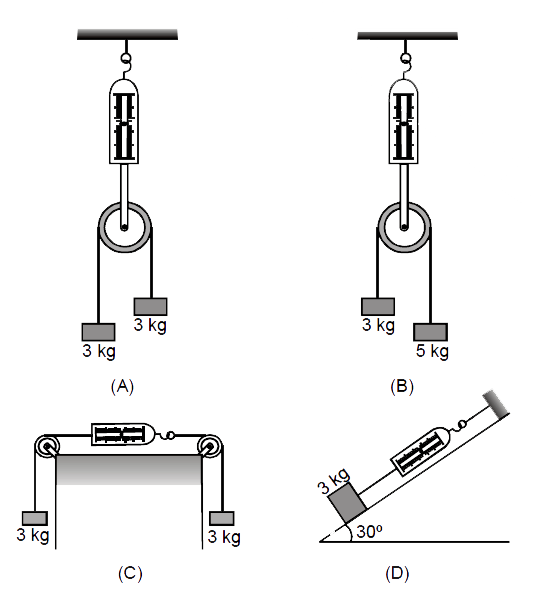
Assume that
Pulleys are massless and frictionless
Strings are massless
The surface in figure (D) is frictionless
Reading of the spring scale in figure (B) is
View SolutionIn the systems shown in figure (A), (B), (C) and (D), the scales of the springs are calibrated in newton Assume that Pulleys are massless and frictionless Strings are massless The surface in figure (D) is frictionless Reading of the spring scale in figure (C) is
View SolutionIn the systems shown in figure (A), (B), (C) and (D), the scales of the springs are calibrated in newton Assume that Pulleys are massless and frictionless Strings are massless The surface in figure (D) is frictionless Reading of the spring scale in figure (D) is
View Solution
