Assume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion. Solution in Tamil
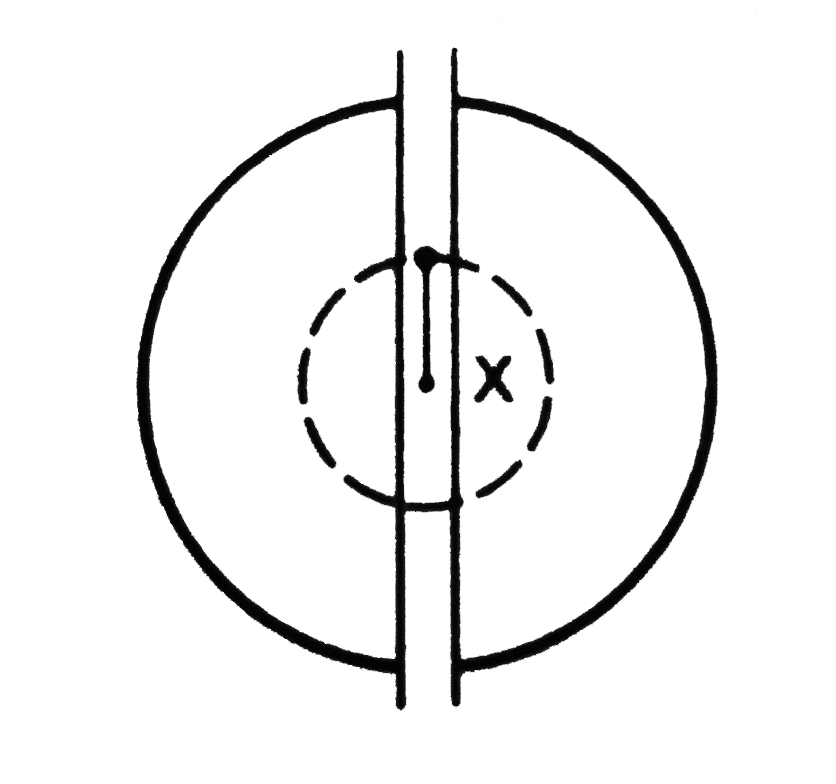Consider the situation shown in ure. Suppose at an instant t the particle in the tunnel is at a distance x from the centre of the earth. Let us draw a sphere of erradius x with its centre at the centre of the earth. Only the part of the earth within this sphere will exert a net attraction on the particle. Mass of this part is
M'=43πx343πR3M=x3R3M
The force of attraction is therefore
F=G(x3r3)Mm^2=GMmR3x
This force acts towards the centre of the earth. Thus, the resultant force on the particle is opposite to the displacement from the centre of the earth and is proportioN/Al to it. The particle therefore executes a simple harmonic motion in the tunnel with the centre of the earth as the mean position.
The force constant is k=GMmR3 so that the time period is
T=2π√mk=2π√R3GM
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer17videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -121videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
A person goes to bed at shasrp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no why?
04:57View SolutionA student says that he had applied a force F=−k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
04:45View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
02:09View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
05:06View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
03:36View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
02:28View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
01:04View SolutionImagine a tunnel dug along a diameter of the earth. Show that a particle dropped from one end of the tunnel executes simple harmonic motion. What is the time period of this motion? Assume the earth to be a sphere of uniform mass density (equal to its known average density=5520 kg m^(-3) .)G= 6.67xx10^(-11)Nm^(2)kg^(-2) .Neglect all damping forces.
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it Time period of the particle is not equal to
04:01View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it Maximum speed of the particle is
01:08View SolutionA tunnel is dug through the centre of the earth. Shwo that a body of mass m when dropped form rest from one end of the tunnel will execute simple harmonic motion.
View SolutionImagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
05:02View SolutionA smooth-walled tunnel is made along the straight line connecting any two points on the earth's surface. A body is released at one end of the tunnel. Considering the earth to be a sphere of uniform density, calculate the time period of oscillation of the particle for its simple harmonic motion.
07:20View SolutionA tunnel is dug through the centre of the earth. Show that a body of mass m when dropped from rest from one end of the tunnel will execute simple harmonic motion.
04:59View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
04:48View SolutionA particle of mass m is released through a narrow tunnel dug between two diametrically opposite ends of Earth. Show that it will exceute SHM and calculate its time period?
00:29View Solution