The square lamina of side 'b' has same mass as a disc of radius R. The M.I. of the two about an axis perpendicular to the plane and passing throught the centre are equal. The ratio b/R is
1
√6
√3
1/3
The correct Answer is:C
I=M12(b2+b2)
=M122b2
∴MR22=M2b212
∴bR=√3
Topper's Solved these Questions
Similar Questions
Find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is I. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View Solution
Knowledge Check
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3What is the ratio of the moments of inertia of two rings radii r and nr about an axis perpendicular to their plane and passing through their centres?
A1:n2B1:nC1:2nDn2:1The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A12MR2B14MR2CMR2D34MR2
A rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
View SolutionFrom a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
View SolutionM.I. of a thin uniform circular disc about one of the diameters is I. Its M.I. about an axis perpendicular to the plane of disc and passing through its centre is
View SolutionThe M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
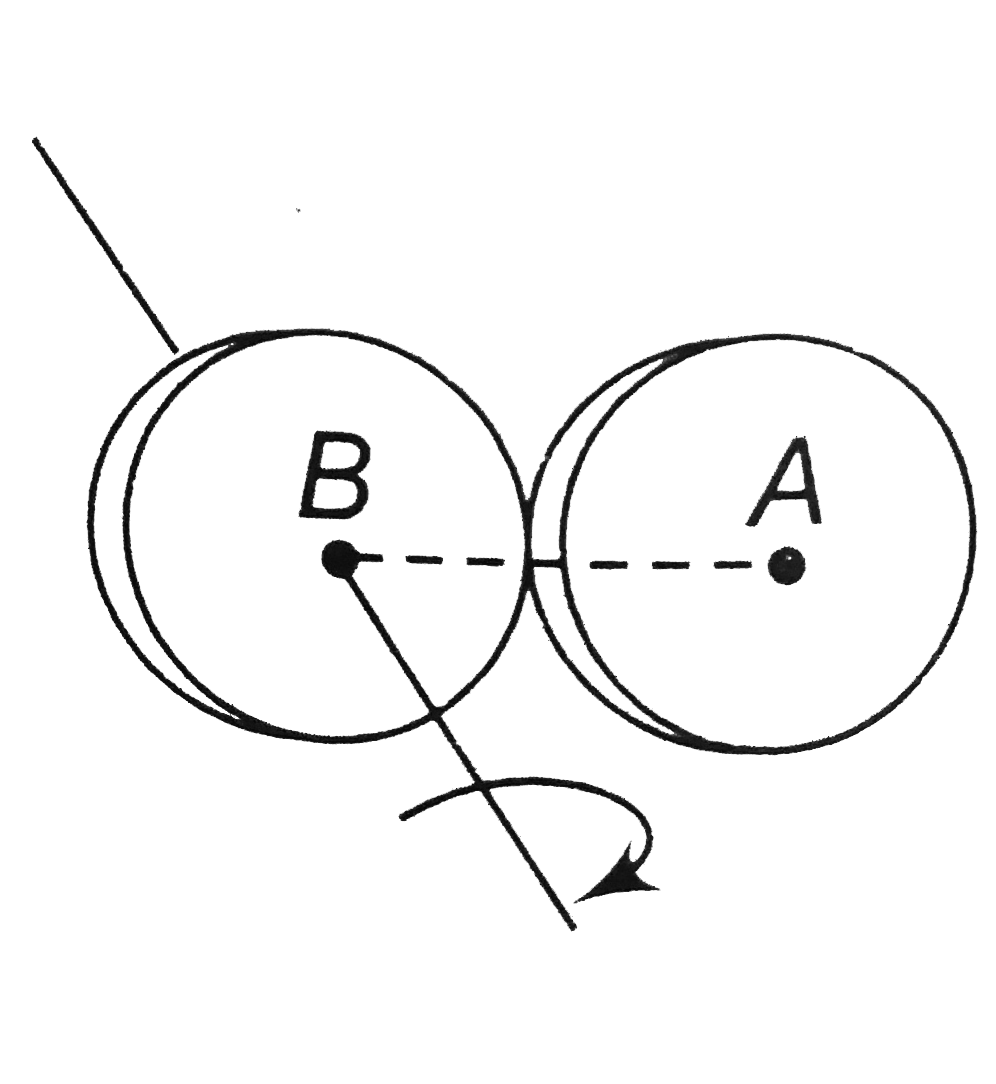 .
.
View Solution
