The switch is closed at t=0. The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) ln2 (B) 12ln(2) (C) 14ln(2) (D) 2ln2
Step by step video solution for The switch is closed at t = 0. The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) ln2 (B) (1)/(2) ln(2) (C) (1)/(4) ln(2) (D) 2ln2 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Consider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
View SolutionThe graph between log t1/2 and log a at a given temperature is
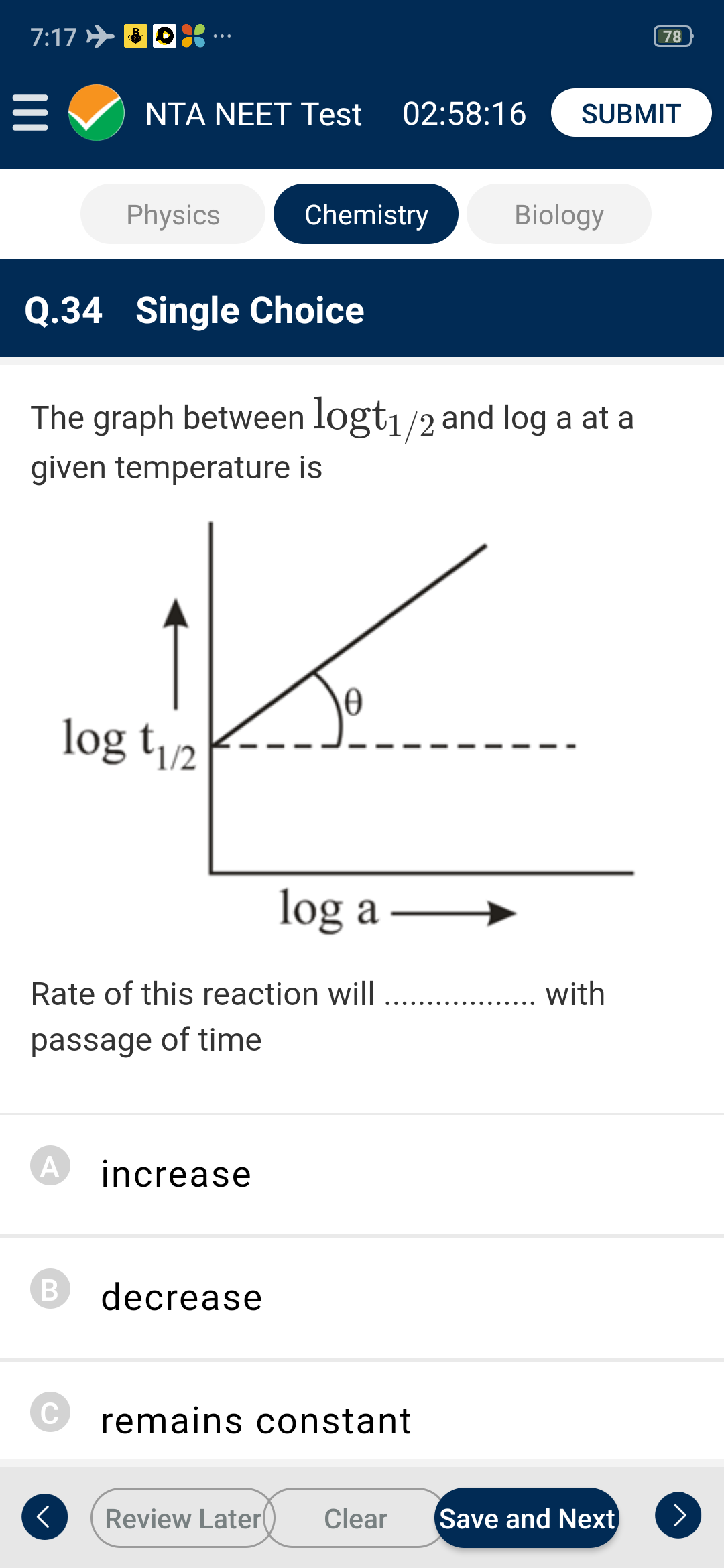
Rate of this reaction will …….with passage of time
View SolutionFind the domain of f(x)=(log)10(log)2(log)2π(tan−1x)−1
View Solution∫42⎛⎝(log)x2−((log)22)2ln2⎞⎠dx= 0 (b) 1 (c) 2 (d) 4
View SolutionThe value of ∫√ln3√ln2xsinx2sinx2+sin(ln6−x2)dx is (A) 14ln(32) (B) 12ln(32) (C) ln(32) (D) 16ln(32)
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
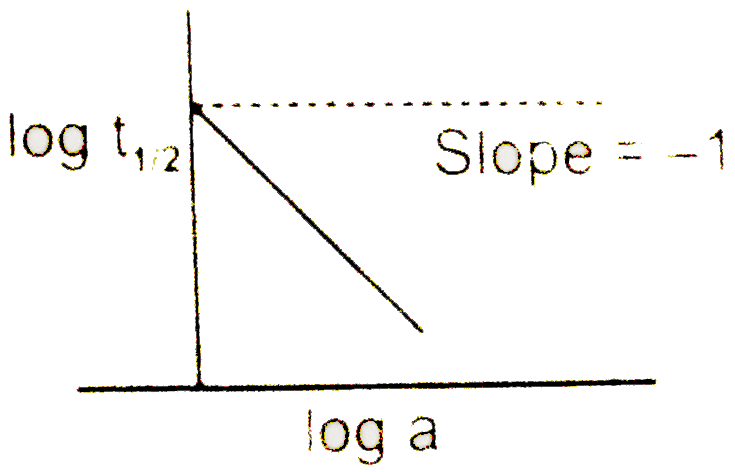
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :

View SolutionThe number of solutions of (log)4(x−1)=(log)2(x−3) is (a) 3 (b) 1 (c) 2 (d) 0
View SolutionIf p>1 and q>1 are such that log(p+q)=logp+logq,then the value of log(p−1)+log(q−1) is equal to (a) 0 (b) 1 (c) 2 (d) none of these
View SolutionIf (log)45=aand(log)56=b, then (log)32 is equal to 12a+1 (b) 12b+1 (c) 2ab+1 (d) 12ab−1
View Solution
