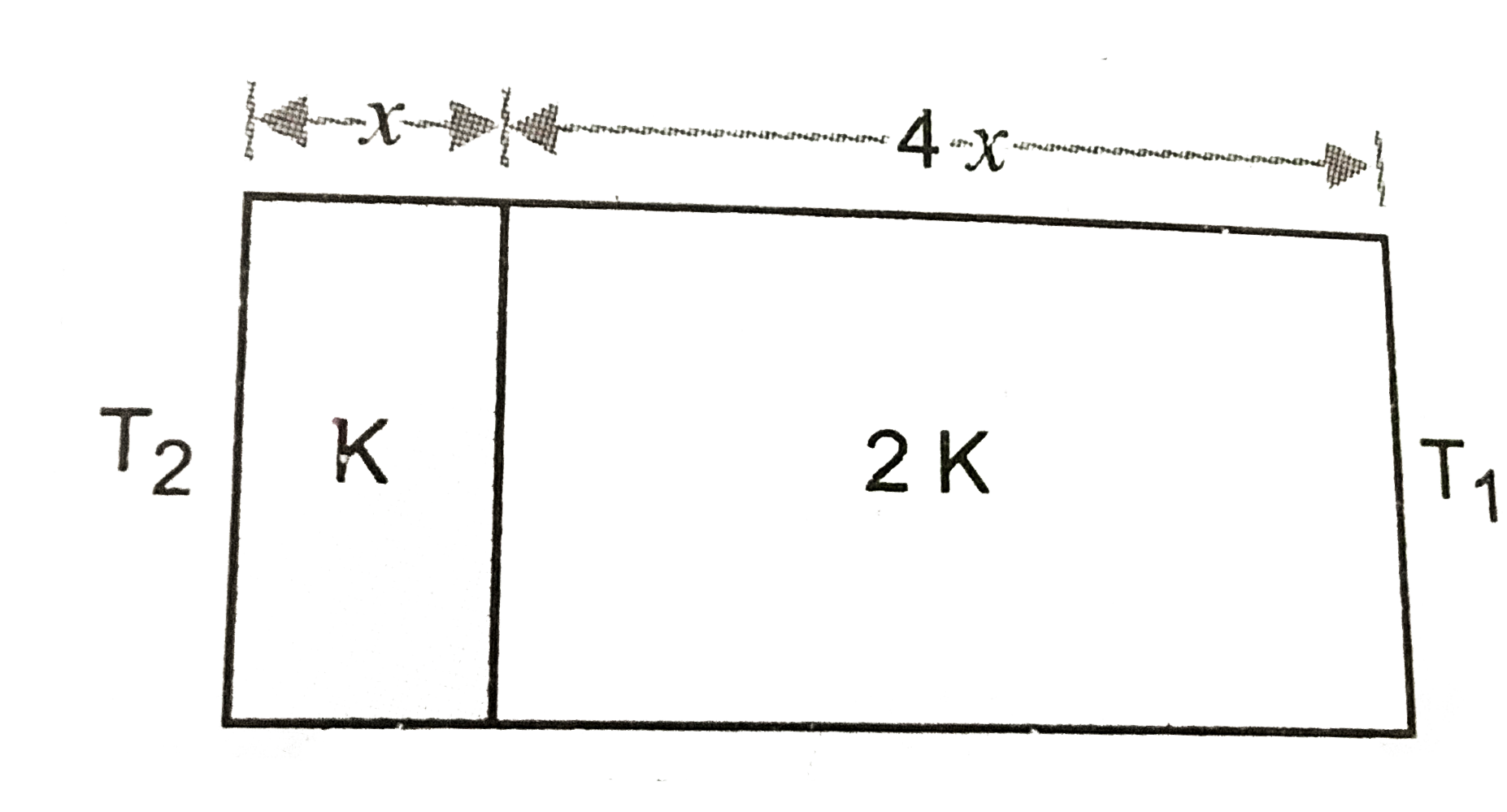
The temperature of the two outer surfaces of a composite slab, consisting of two materails having coefficients of two materails having coefficients of termal conductivity K and 2K and thickness x and 4x, respectively, are T2andT1(T1>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)K2)f, with f equal to

23
12
1
13
The correct Answer is:D
(d) The thermal resistance
xKA+4x2KA=3xKA
∴dQdt=ΔT3xKA=(T2−T1)KA3x=13{A(T2−T1)Kx}
∴f=13
Topper's Solved these Questions
Similar Questions
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
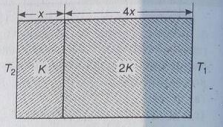 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .A1B1/2C2/3D1/3
.A1B1/2C2/3D1/3
Two materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
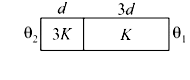
View SolutionA composite slab consists of two rectangular slabs of different materials, having coefficients of conductivity 2K and K. The two ends of the slabs are at temperatures T1 and T2 (where T1>T2 ). How will the rate of heat flow depend on a where 3a and a are the lengths of two slabs? Consider that the two slabs have equal thickness.

View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution
