The time period of a simple pendulum in a stationary train is T. The time period of a mass attached to a spring is also T. The train accelerates at the rate 5 ms−2. If the new time periods of the pendulum and spring be TpandTs, respectively. Then,
Tp=Ts
Tp>Ts
Tp<Ts
Cannot be predicted
The correct Answer is:C
Time period of simple pendulum placed in a train accelerating at the rate of a ms−2 is given by

T=2π[I√g2+a2]12
It is independent of g as well as a. Hence, when the train accelerates, the time period of the simple pendulum decreases and that of spring remains unchanged.
Hence, Tp<T
and Ts=T i.e.Tp<Ts
Topper's Solved these Questions
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - EXERCISE 2
49 Videos
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - MHT CET CORNER
29 Videos
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - MHT CET CORNER
29 Videos
- MOCK TEST 5BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MOCK TEST 5EXERCISE - MCQs
42 Videos
- PRACTICE SET 01BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 01EXERCISE - PAPER 1 (PHYSICS & CHEMISTRY)
50 Videos
Similar Questions
Knowledge Check
The time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes
A0.98TB1.02TC0.99TD1.01TThe time period of a simple pendulum inside a stationary lift is T. If it starts descending with acceleration g/5. the new period of the simple pendulum will be
A2TB√52TC√53TD2√5TA man measures the period of a simple pendulum inside a stationary lift and find it be T. If the lift accelerates downwards with an acceleration of g/3, then the period of the pendulum will be
A√2TBT√2C√32TDT3
The graph of time period (T) of a simple pendulum versus its length (I) is
View SolutionThe time period of simple pendulum inside a stationary lift is T. If lift starts accelerating upwards with the acceleration of g/2, then the new time period of the simple pendulum will be
View SolutionThere is a simple pendulum hanging from the ceiling of a lift. When the lift is stand still, the time period of the pendulum is T . If the resultant acceleration becomes g/4 ,then the new time period of the pendulum is
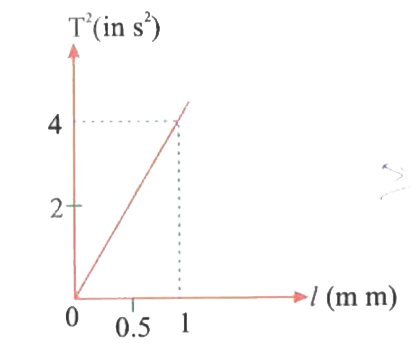
View SolutionThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
View SolutionThe time period of a simple pendulum measured inside a stationary lift is found to be T . If the lift starts accelerating upwards with an acceleration g/3, the time period is
View Solution
