The top of the atomosphere is about 400 kV with respect to the surface of earth, corresponding to an electric field that decreases with altitude. Near the surface of earth the field is about 100 V m−1, but still don't get an electric shock, as we set out of out houses in to open because (assume the house is free from electric field)
our body is a perfect insulator
our body and ground form an equipotential surface
the original equipotential surfaces of open air remain same
none of these
The correct Answer is:B
Since, our body and the surface of earth, both are conducting , therefore our body and the ground form an equipotential surface. As we step out in to the open from our house, the original equipotential surfaces of open air change , keeping our body and the ground at the same potential. That is why we do not get an electric shock .
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
The radius of a gold nucleus (Z=79) is about 7.0⋅10−10m. Assume that the positive charge is distributed uniformly throughout the the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
View SolutionConsider a point charge q=1mC placed at a corner of a cube of sides 10 cm . Determine the electric flux through each face of the cube.
Strategy : We will learn about the utility of symmetry in solving problems with the help of Gauss's law . Here we'll use the symmetry of the situation,which involves the faces joining at the corner at which the charge resides.

(a) A charge q is placed atthe corner of a cube. (b) By surrounding the charge with a series of cubes such that the charge is at the centre of a larger cube, we have created an arrangement sufficiently symmetric to be able to solve for desired flux values.
You can see from figure that for these faces →E.ˆn=0. Since the normal is perpendicular to the surfaces while the electric field goes off in a spherically symmetric pattern and lies in the sides . In other words , the electric field that originates at the charge is tangential to the surface of these three sides. This means there is no flux through these sides. The electric flux through each of the remaining three faces of the be must be equal by symmetry . We'll referto these faces with the label F.
To fidn the flux through each of the sides F, we acan use a technique that puts the single charge in the middle of a larger cube. It takes seven other similarly placed cubes to surrounds the points charge q completely in figre. The charge is at the dead centre of the enw larger cube. So, the flux through each of the six sides of the large cube will now have an electric flux of one sixth of the total flux F. So given that the total structure is completely symmetric, the flux through a side F is one fourth of the flux through the larger side.
View SolutionIf the electric field intensity in a fair weather atmosphere is 100 V/m, then total charge on the earth's surface is (radius of the earth is 6400 km)
View SolutionIt has been experimentally observed that the electric field in a large region of earth's atmosphere is directed vertically down. At an altitude of 300 m, the electric field 60Vm−1. At an altitude of 200 m, the field is 100 V m^(-1), the field is 100Vm−1. Calculate the net amount of charge contained in the cube of 100 m edge, located between 200 and 300 m altitude.

View SolutionThe earth's surface has a negative surface charge density of 10−9Cm−2 . The potential difference of 400 kV between the top of the atmosphere and the surface results (due to low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmosphereic electric field , how much time (roughly) would be required to neutralise the earth's surface ? (This never happens in practice because there is a mechanism to replenish electric charges namely the continual thunder storms and lightning in different parts of the globe). Radius of the earth =6.37×106m.
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and −q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
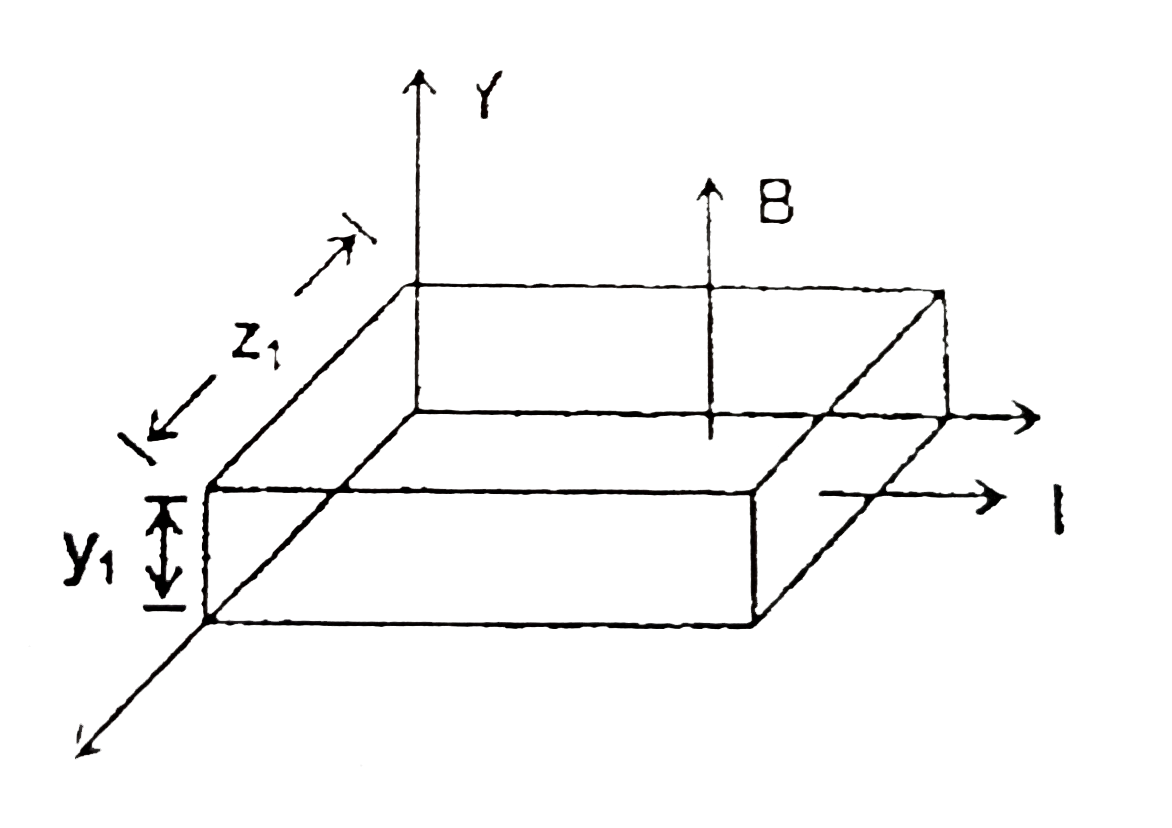
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
Magnitude of the drift velocity of elelctrons is
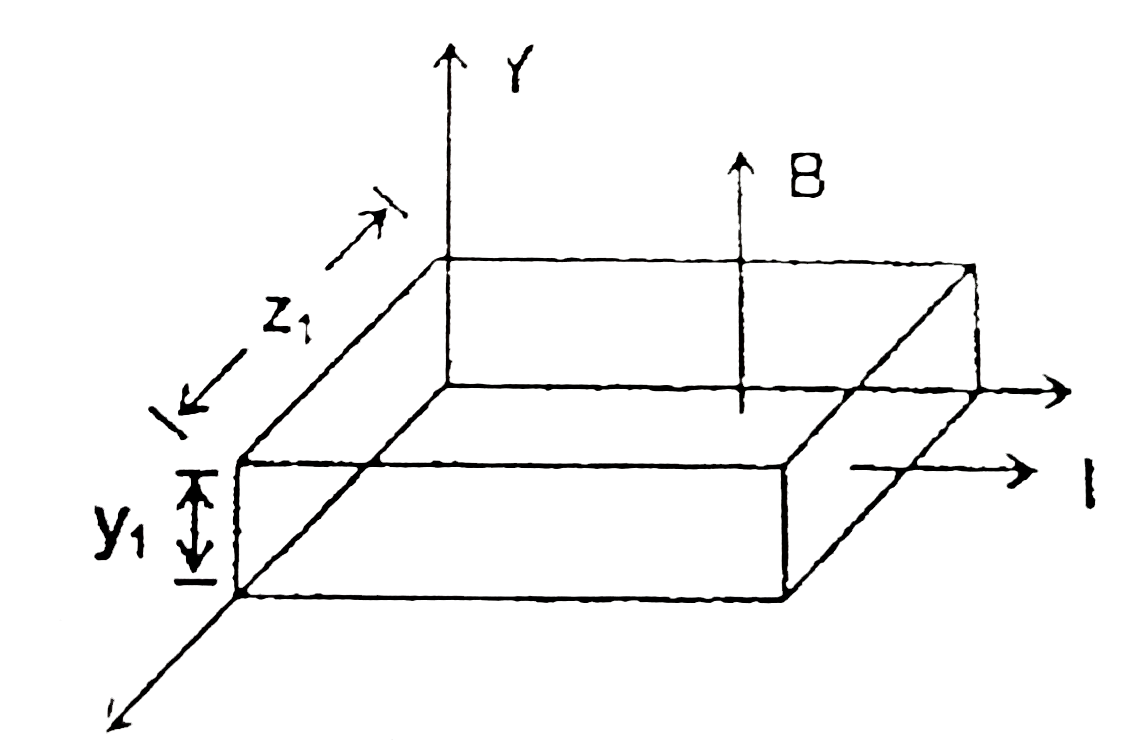
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
What is the value of hall emf ?
View SolutionWhen liquid medicine of density ρ is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If r=5×10−4m,ρ=103kgm−3,g=10ms−2,T=0.11Nm−1, The radius of the drop when it detaches from the dropper is approximately,
View Solution
