Question

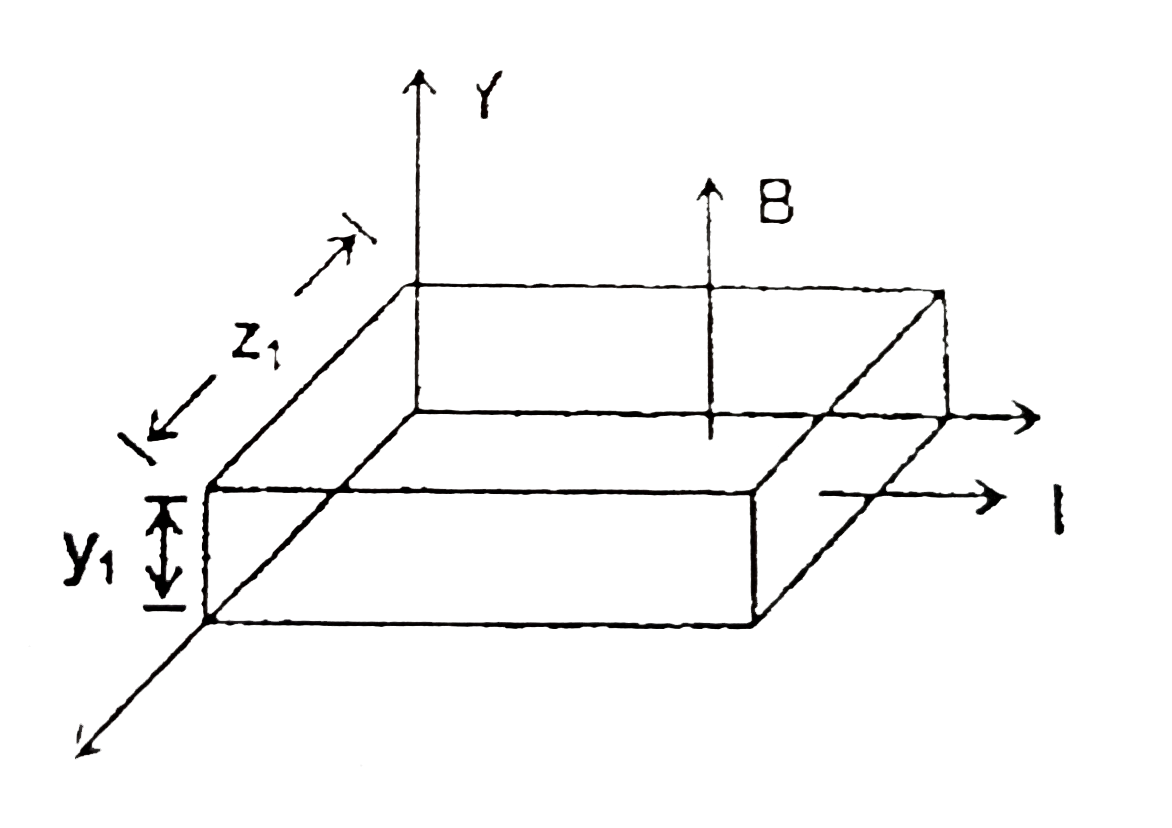
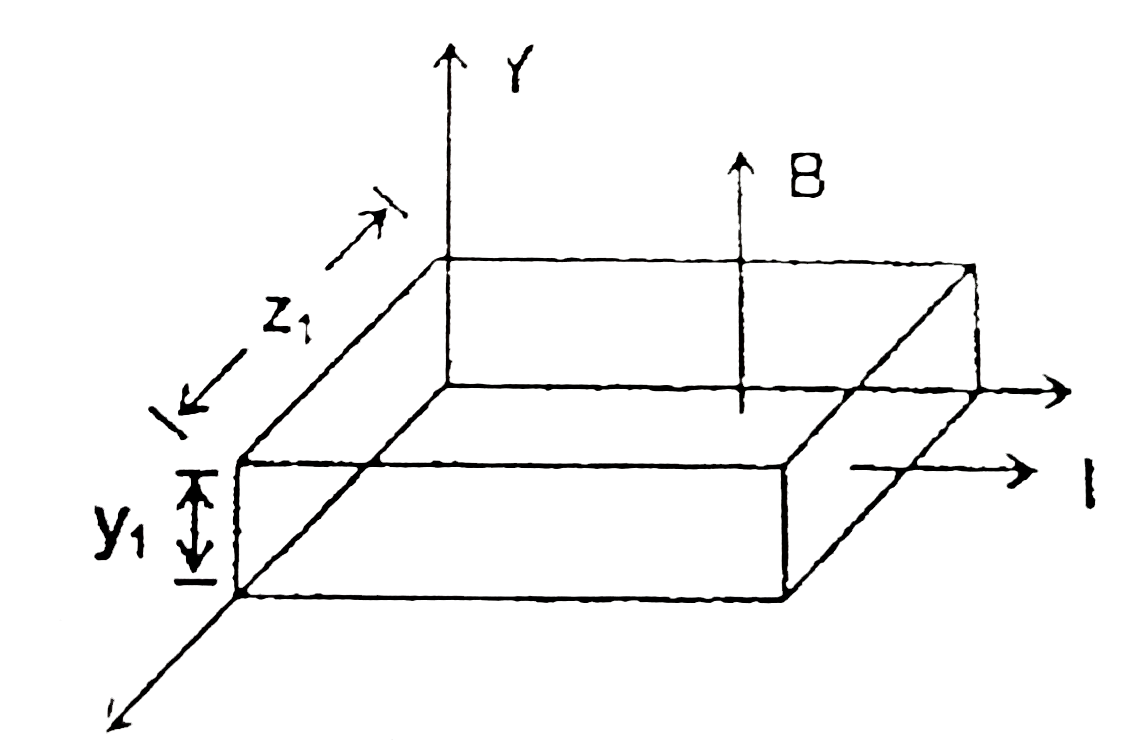
The basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an $n$-type, $\text{bar}$-shaped semiconductor, the carriers are predominantly electrons of bulk density $n$. We assume that the constant current $I$ flows along the $x$-axis from left to right in the presence of a magnetic field toward $y$-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative $z$-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage $V_H$ and its magnitude is equal to $IB/qnd$, where $I$ is the current, $B$ is the magnetic field, $d$ is the sample thickness and $q$ is the elementary charge. A silver ribbon lies as shown in the adjacent figure. ($z_1=11.8mm$ and $y_1=0.23mm$) carrying a current of $120A$ in the $x$-direction in a uniform magnetic field $B=0.95T$. If electron density is $5.85\times {10}^{28}/m^3$, then
Magnitude of the drift velocity of elelctrons is

Options

A. `2.35 mm//s`
B. `4.7 mm//s`
C. `7.05 mm//s`
D. `9.4 mm//s`