The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ=0 or θ=180∘. In which of the two orientations, the equilibrim is stable?
To determine the stability of equilibrium for a current loop in a magnetic field, we can follow these steps:
Step 1: Understand the Torque on a Current Loop
The torque (τ) on a current loop in a magnetic field is given by the equation:
τ=→m×→B
where →m is the magnetic moment and →B is the magnetic field. The magnitude of the torque can also be expressed as:
τ=mBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
Step 2: Identify the Conditions for Zero Torque
The torque is zero when:
- θ=0∘ (the magnetic moment is parallel to the magnetic field)
- θ=180∘ (the magnetic moment is antiparallel to the magnetic field)
Step 3: Determine Potential Energy
The potential energy (U) of the current loop in the magnetic field is given by:
U=−→m⋅→B=−mBcosθ
To find stable and unstable equilibrium, we need to analyze the potential energy.
Step 4: Analyze Stability Conditions
- Stable Equilibrium: Occurs when potential energy is at a minimum.
- Unstable Equilibrium: Occurs when potential energy is at a maximum.
Step 5: Find the Values of U at θ=0∘ and θ=180∘
1. For θ=0∘:
U=−mBcos(0)=−mB⋅1=−mB(minimum potential energy)
2. For θ=180∘:
U=−mBcos(180)=−mB⋅(−1)=mB(maximum potential energy)
Step 6: Conclusion
Since the potential energy is minimum at θ=0∘ and maximum at θ=180∘, the equilibrium is stable at θ=0∘ (when the magnetic moment is parallel to the magnetic field).
Final Answer
The equilibrium is stable when the angle θ=0∘.
---
The torque (τ) on a current loop in a magnetic field is given by the equation:
τ=→m×→B
where →m is the magnetic moment and →B is the magnetic field. The magnitude of the torque can also be expressed as:
τ=mBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
The torque is zero when:
- θ=0∘ (the magnetic moment is parallel to the magnetic field)
- θ=180∘ (the magnetic moment is antiparallel to the magnetic field)
The potential energy (U) of the current loop in the magnetic field is given by:
U=−→m⋅→B=−mBcosθ
To find stable and unstable equilibrium, we need to analyze the potential energy.
- Stable Equilibrium: Occurs when potential energy is at a minimum.
- Unstable Equilibrium: Occurs when potential energy is at a maximum.
1. For θ=0∘:
U=−mBcos(0)=−mB⋅1=−mB(minimum potential energy)
2. For θ=180∘:
U=−mBcos(180)=−mB⋅(−1)=mB(maximum potential energy)
Since the potential energy is minimum at θ=0∘ and maximum at θ=180∘, the equilibrium is stable at θ=0∘ (when the magnetic moment is parallel to the magnetic field).
The equilibrium is stable when the angle θ=0∘.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - Exercises60videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
The force exerted on a current-carrying wire placed in magnetic field is zero when the angle between the wire and the direction of magnetic field is :
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

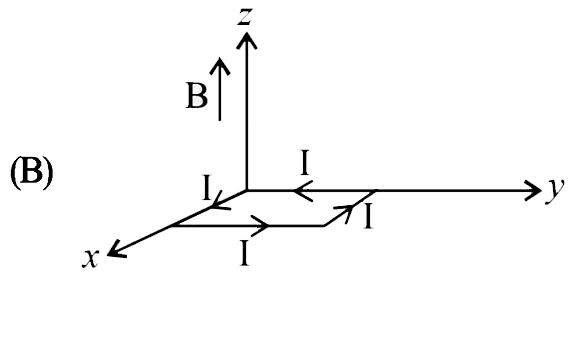

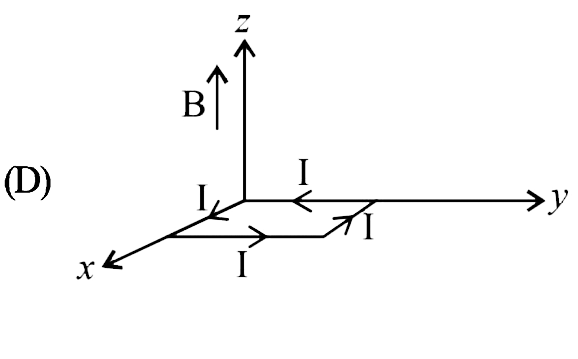 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular loop of sides 10cm and 5cm carrying a current I of 12A is placed in different orienctations as shown in the figure
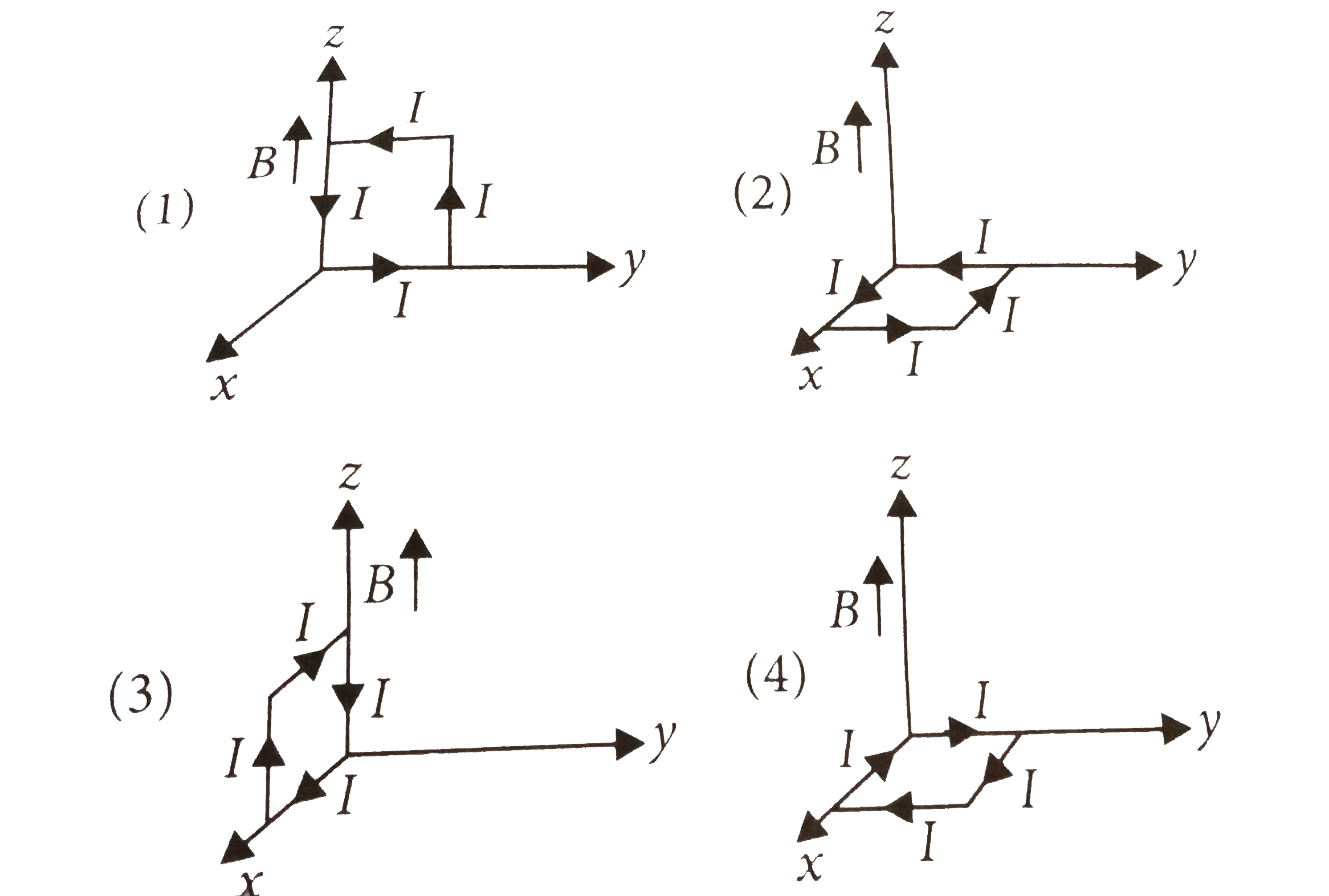
If there is a uniform magnetic field of 0.3 T in the positive z-direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium .A(2)and(4), respectivelyB(2)and(3), respectivelyC(1)and(2), respectivelyD(1)and(3), respectively
A rectangular loop of sides 10 cm and 5 cm carrying a current 1 of 12 A is placed in different orientations as shown in the figures below :
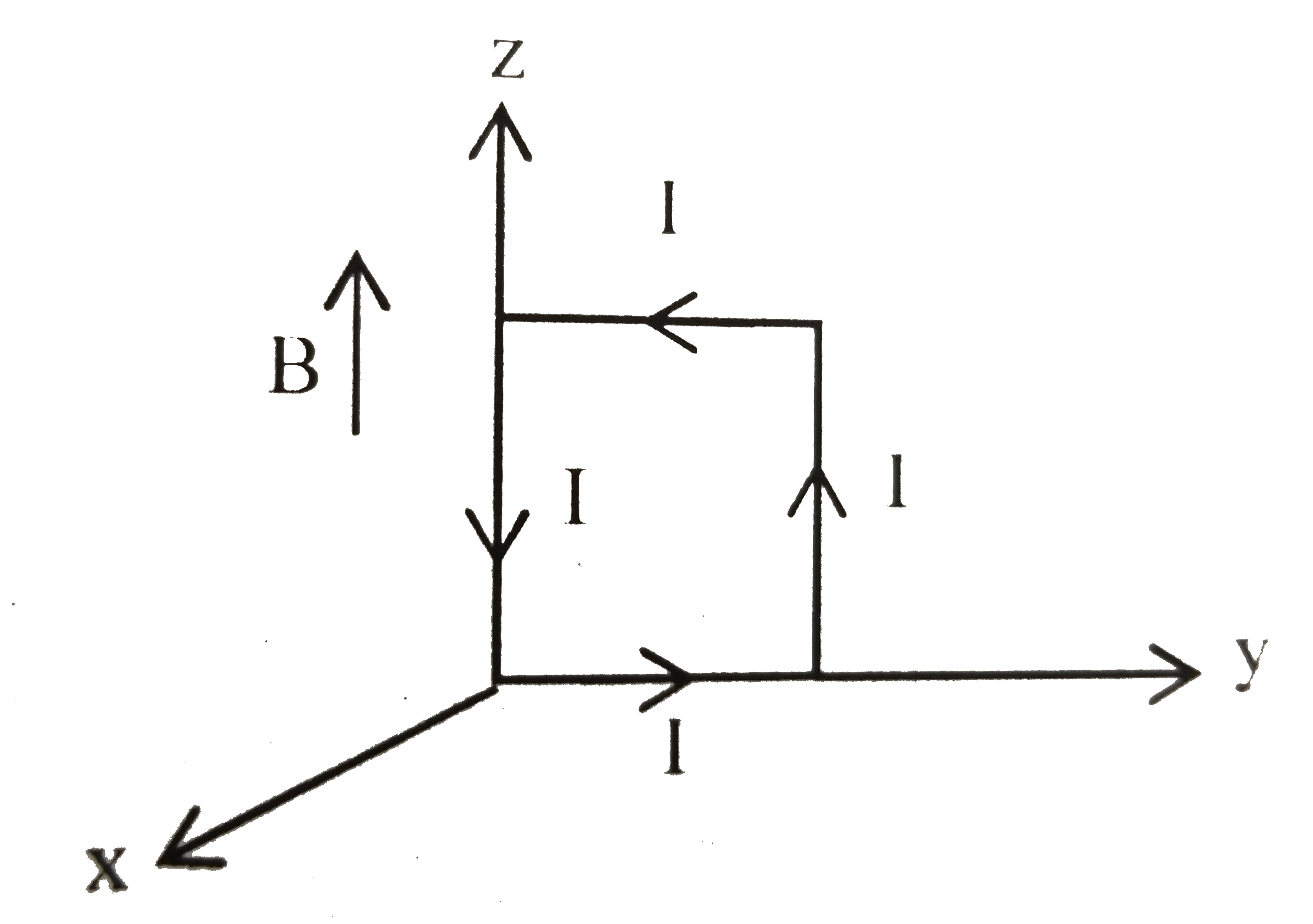
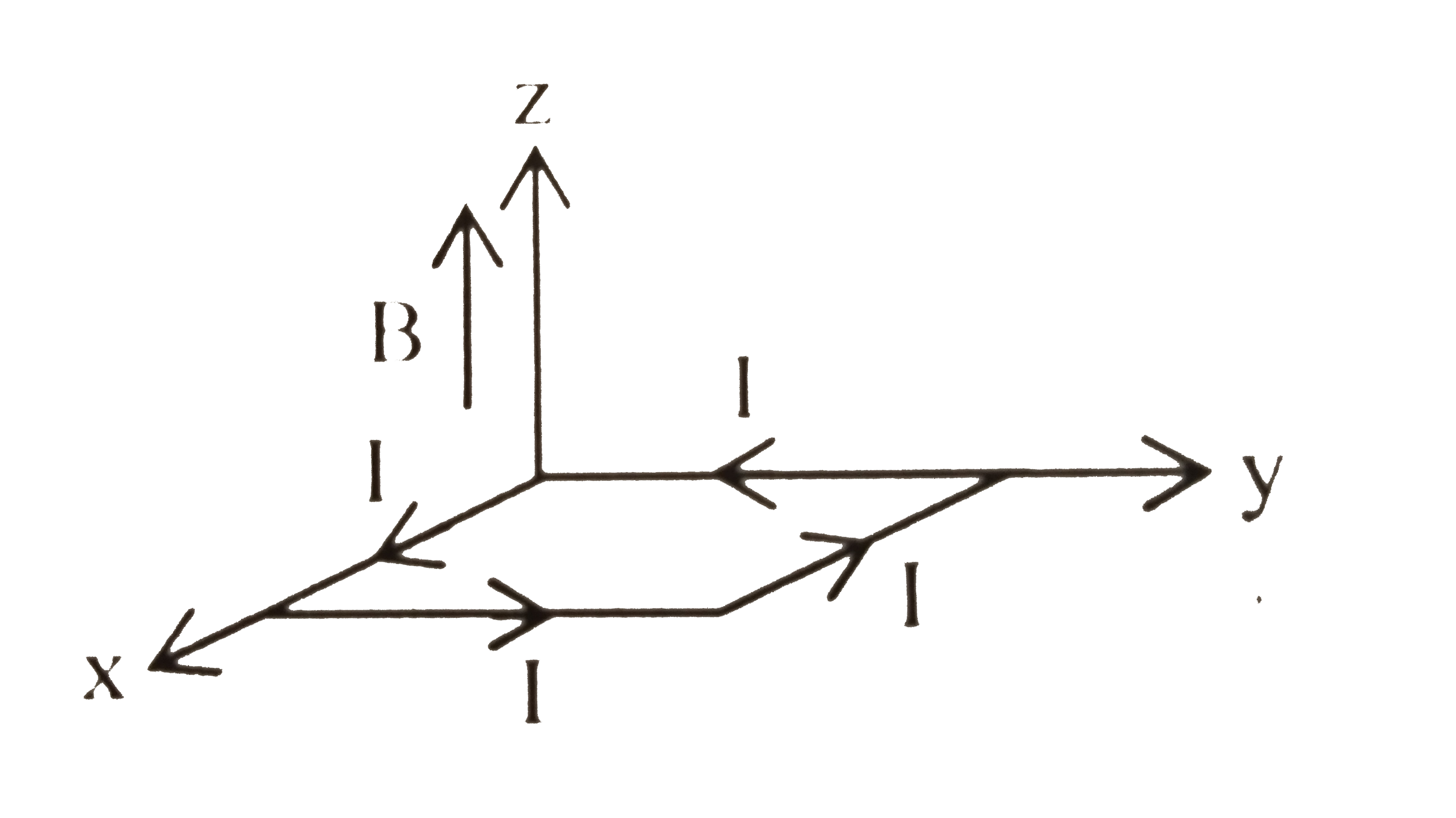
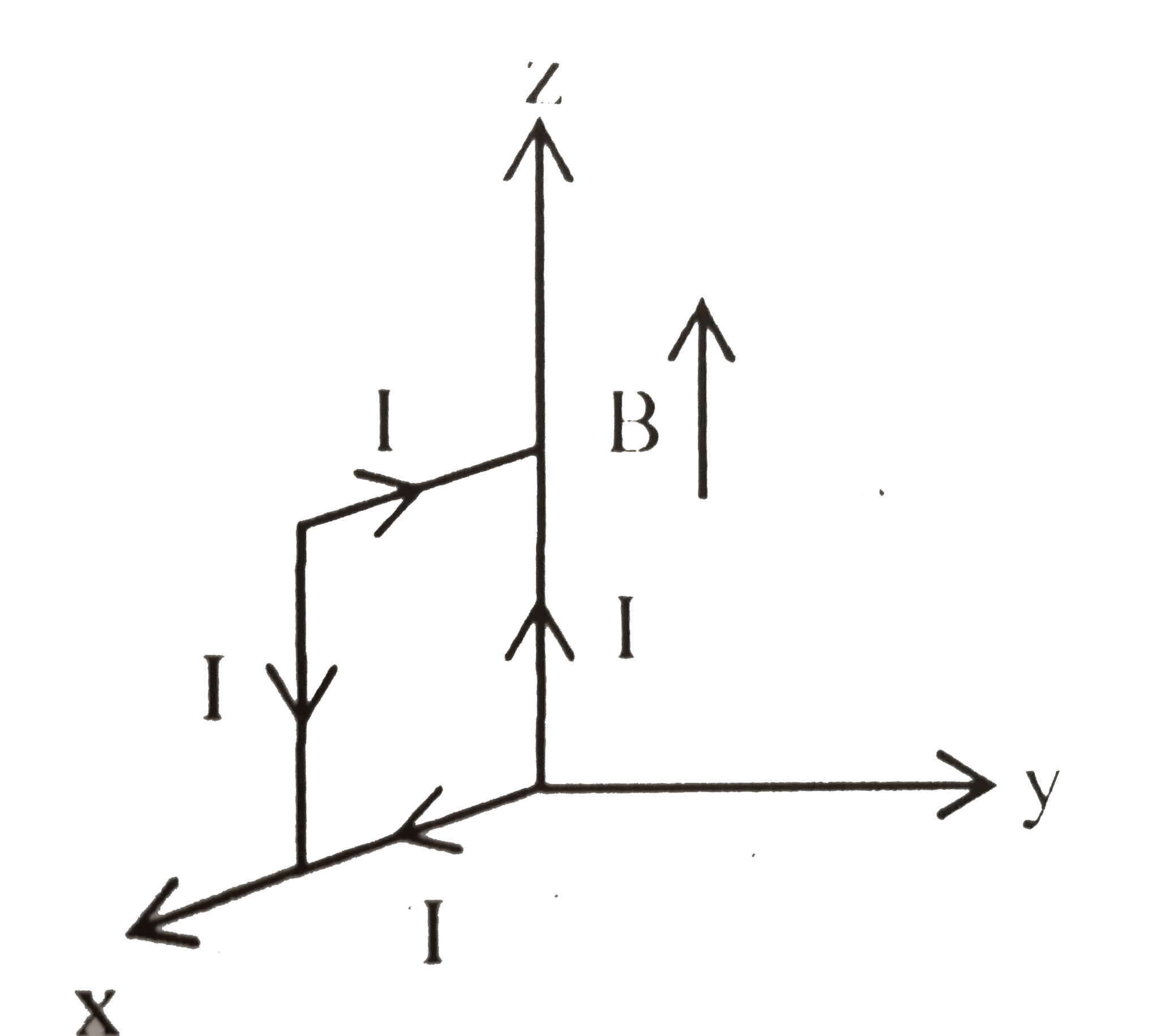
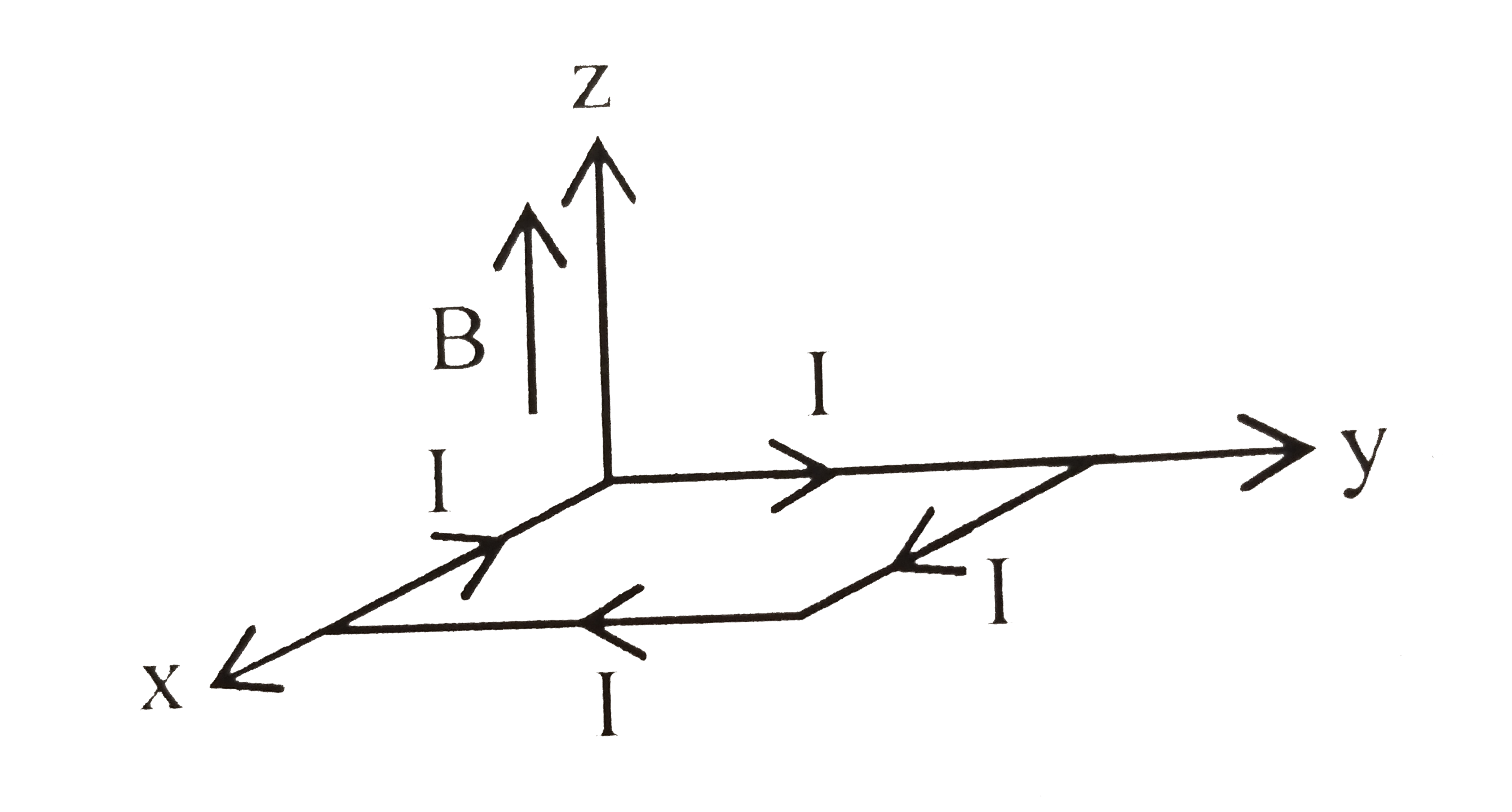 ltBrgt If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium ?View Solution
ltBrgt If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium ?View SolutionThe path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
Two ions having masses in the ratio 1:1 and charges 1:2 are projected from same point into a uniform magnetic field with speed in the ratio 2:3 perpendicular to field. The ratio of radii of circle along which the two particles move is :View SolutionThe path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
A charged particle moves in a uniform magnetic field. The velocity of particle at some instant makes acute angle with magnetic field. The path of the particle will beView SolutionThe path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
Which particle will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field.View SolutionA bar magnet of magnetic moment 6 J/T is aligned at 60∘ with a uniform external magnetic field of 0.44 T. Calculate (a) the work done in turning the magnet to align its magnetic moment (i) normal to the magnetic field, (ii) opposite to the magnetic field, and (b) the torque on the magnet in the final orientation in case (ii).
View SolutionForce on current carrying loop (Radius = R) in uniform magnetic (B) field which is at an angle 30” with the normal will be :-
View SolutionMention the angle between a current carrying conductor and magnetic field for which the force experienced by this current conductor placed field is largest ?
View Solution

