Force on current carrying loop (Radius = R) in uniform magnetic (B) field which is at an angle 30” with the normal will be :-
zero
2πRiB
2√3πRiB
πRiB
The correct Answer is:A
To solve the problem of finding the force on a current-carrying loop of radius R in a uniform magnetic field B that is at an angle of 30∘ with the normal to the plane of the loop, we can follow these steps:
1. Understanding the Setup:
- We have a circular loop of radius R carrying a current I.
- The loop is placed in a uniform magnetic field B which makes an angle of 30∘ with the normal to the plane of the loop.
2. Magnetic Force on a Current-Carrying Loop:
- The magnetic force F on a current-carrying conductor in a magnetic field is given by the formula:
F=I(L×B)
- For a closed loop, the net force can be calculated using the magnetic moment m of the loop.
3. Magnetic Moment:
- The magnetic moment m of the loop is given by:
m=I⋅A
- Where A is the area of the loop. For a circular loop:
A=πR2
- Thus,
m=I⋅πR2
4. Torque on the Loop:
- The torque τ experienced by the loop in the magnetic field is given by:
τ=m⋅B=mBcos(θ)
- Here, θ is the angle between m and B. In this case, θ=30∘.
5. Force Calculation:
- However, the key point is that the net force on a closed current-carrying loop in a uniform magnetic field is zero. This is because the forces on opposite sides of the loop cancel each other out.
- Therefore, regardless of the angle, the total force Fnet=0.
6. Conclusion:
- Hence, the force on the current-carrying loop in the uniform magnetic field at an angle of 30∘ with the normal is:
F=0
Final Answer:
The force on the current-carrying loop in the uniform magnetic field is 0.
- We have a circular loop of radius R carrying a current I.
- The loop is placed in a uniform magnetic field B which makes an angle of 30∘ with the normal to the plane of the loop.
- The magnetic force F on a current-carrying conductor in a magnetic field is given by the formula:
F=I(L×B)
- For a closed loop, the net force can be calculated using the magnetic moment m of the loop.
- The magnetic moment m of the loop is given by:
m=I⋅A
- Where A is the area of the loop. For a circular loop:
A=πR2
- Thus,
m=I⋅πR2
- The torque τ experienced by the loop in the magnetic field is given by:
τ=m⋅B=mBcos(θ)
- Here, θ is the angle between m and B. In this case, θ=30∘.
- However, the key point is that the net force on a closed current-carrying loop in a uniform magnetic field is zero. This is because the forces on opposite sides of the loop cancel each other out.
- Therefore, regardless of the angle, the total force Fnet=0.
- Hence, the force on the current-carrying loop in the uniform magnetic field at an angle of 30∘ with the normal is:
F=0
The force on the current-carrying loop in the uniform magnetic field is 0.
Similar Questions
Knowledge Check
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
A current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA square current carrying loop is suspended in a unifrom magnetic field acting in the plane of the loop. If the force on one arm of the loop is →F, the net force on the remaining three arms of the loop is
View SolutionAssertion : A current carrying loop is placed in uniform magnetic field as shown in figure. Torque in the loop in this case is zero.
Reason : Magnetic moment vector of the loop is perpendicular to paper inwards.
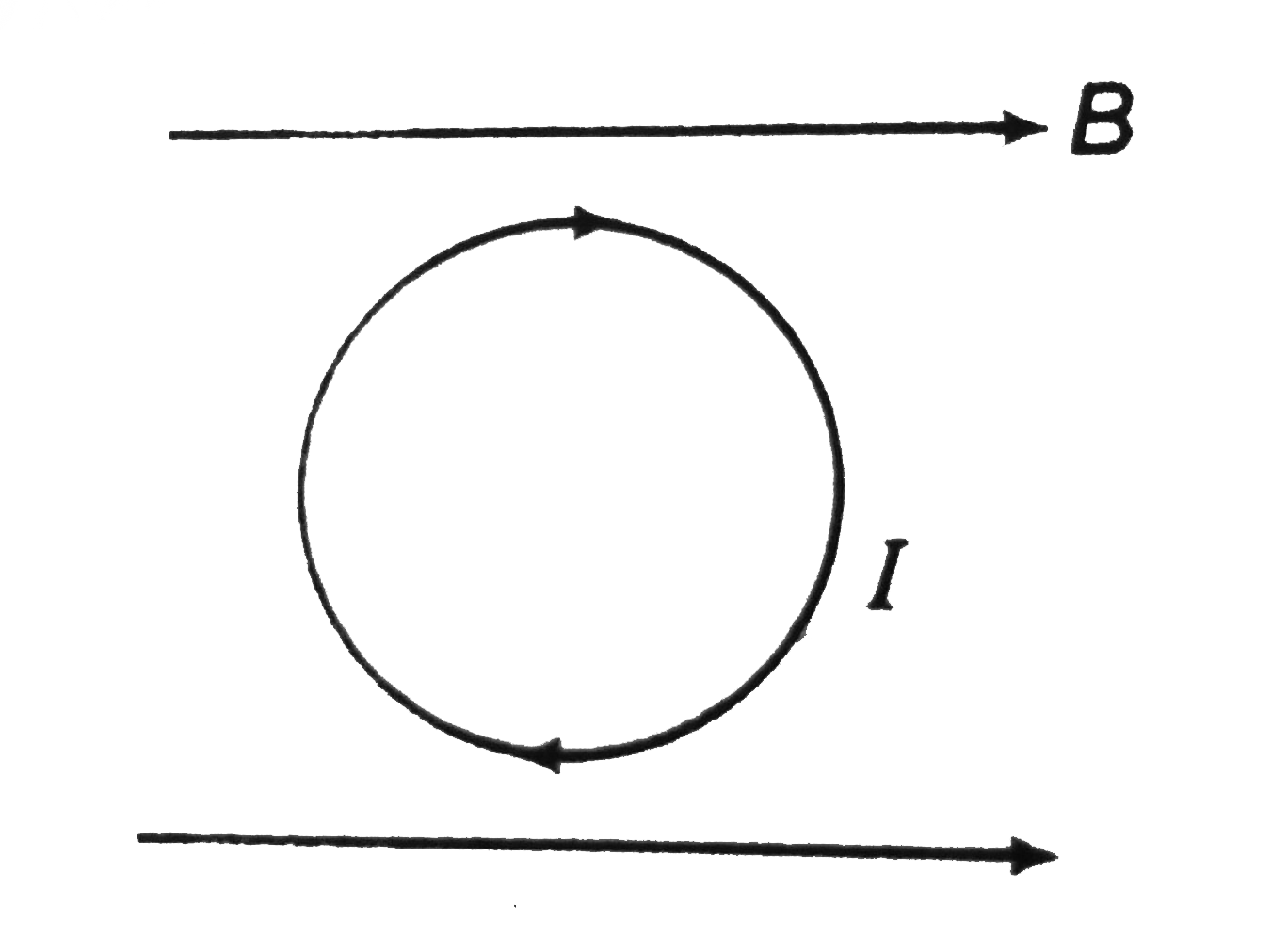
View SolutionWill there be any tension in a current carrying loop placed in uniform magnetic field ? If yes, will it be equal to BiR ?
View SolutionA: Net magnetic force expericneed by a current carrying loop in a uniform magnetic field is always zero.
R. A current loop placed in a uniform magnetic field never experiences a torque.
View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic force experienced by the loop is
View Solution