The velocity of a particle moving in a straight line is decreasing at the rate of 3m/s per metre of displacement at an instant when the velocity is 10m/s. Determine the acceleration of the particle at this instant.
The correct Answer is:B, C
To determine the acceleration of the particle at the given instant, we can follow these steps:
Step 1: Understand the relationship between velocity, displacement, and acceleration.
The problem states that the velocity of the particle is decreasing at a rate of 3ms for every meter of displacement. This can be expressed mathematically as:
\(
\frac{dV}{dS} = -3 \, \text{m/s/m}
\)
Here, dV is the change in velocity, and dS is the change in displacement.
Step 2: Identify the given values.
We are given:
- The velocity \( V = 10 \, \text{m/s} \)
- The rate of change of velocity with respect to displacement \( \frac{dV}{dS} = -3 \, \text{m/s/m} \)
Step 3: Use the relationship between acceleration and the rate of change of velocity with respect to displacement.
Acceleration \( A \) can be expressed as:
\(
A = V \cdot \frac{dV}{dS}
\)
Substituting the known values into this equation will allow us to find the acceleration.
Step 4: Substitute the values into the equation.
Substituting \( V = 10 \, \text{m/s} \) and \( \frac{dV}{dS} = -3 \, \text{m/s/m} \) into the acceleration formula:
\(
A = 10 \, \text{m/s} \cdot (-3 \, \text{m/s/m})
\)
Step 5: Calculate the acceleration.
Now, perform the multiplication:
\(
A = 10 \cdot (-3) = -30 \, \text{m/s}^2
\)
Final Answer:
The acceleration of the particle at that instant is:
\(
A = -30 \, \text{m/s}^2
\)
---
The problem states that the velocity of the particle is decreasing at a rate of 3ms for every meter of displacement. This can be expressed mathematically as:
\(
\frac{dV}{dS} = -3 \, \text{m/s/m}
\)
Here, dV is the change in velocity, and dS is the change in displacement.
We are given:
- The velocity \( V = 10 \, \text{m/s} \)
- The rate of change of velocity with respect to displacement \( \frac{dV}{dS} = -3 \, \text{m/s/m} \)
Acceleration \( A \) can be expressed as:
\(
A = V \cdot \frac{dV}{dS}
\)
Substituting the known values into this equation will allow us to find the acceleration.
Substituting \( V = 10 \, \text{m/s} \) and \( \frac{dV}{dS} = -3 \, \text{m/s/m} \) into the acceleration formula:
\(
A = 10 \, \text{m/s} \cdot (-3 \, \text{m/s/m})
\)
Now, perform the multiplication:
\(
A = 10 \cdot (-3) = -30 \, \text{m/s}^2
\)
The acceleration of the particle at that instant is:
\(
A = -30 \, \text{m/s}^2
\)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
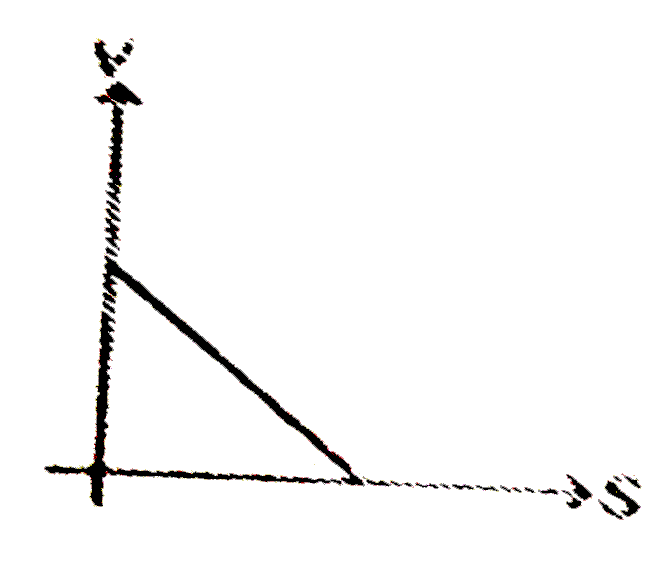 View Solution
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
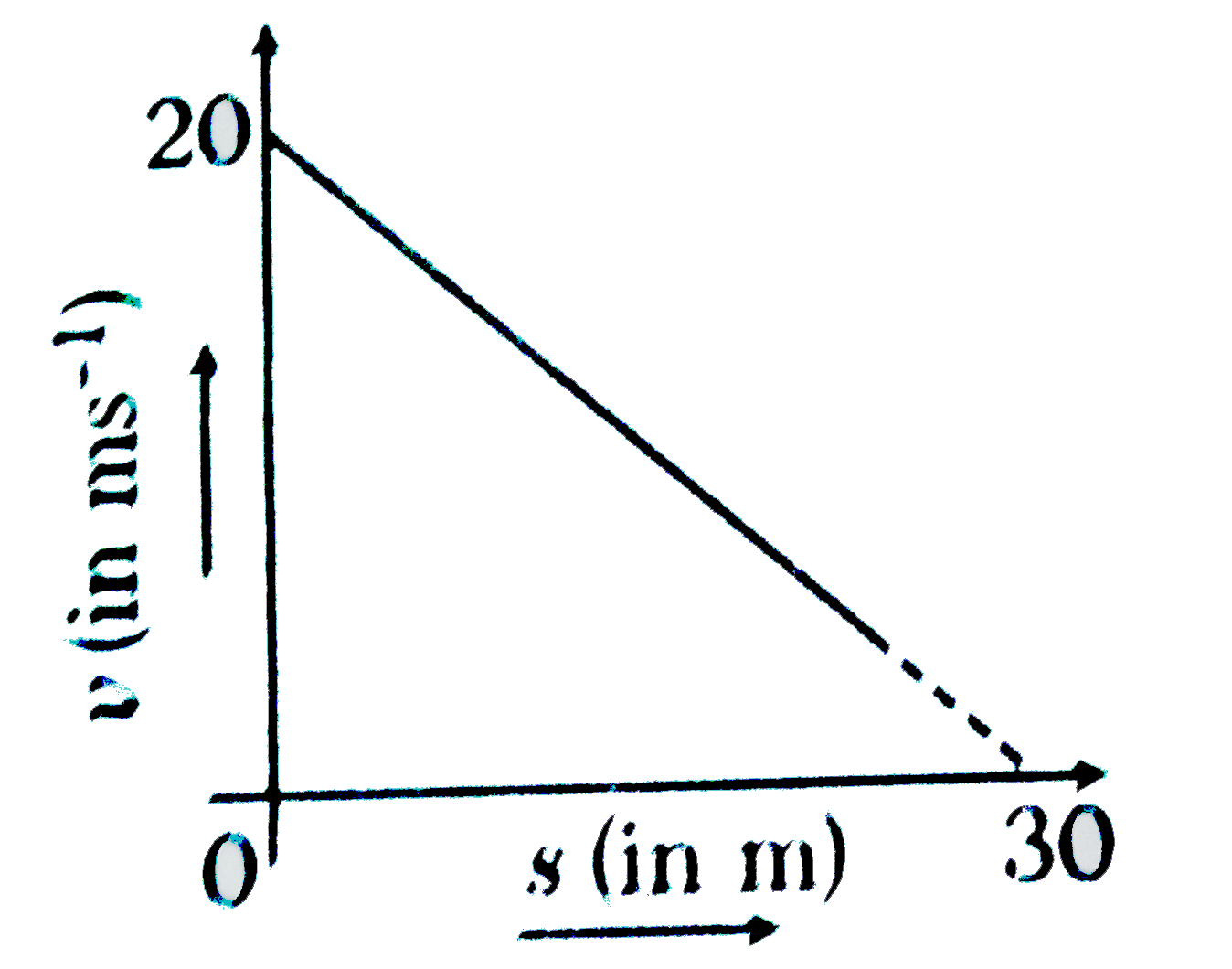 View Solution
View Solution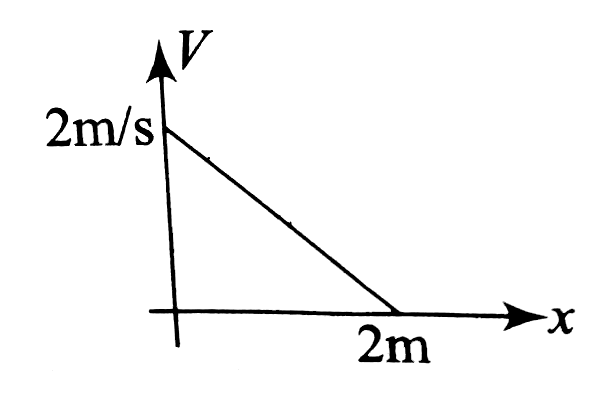
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
 View Solution
View SolutionThe acceleration - velocity graph of a particle moving in a straight line is shown in figure. Then the slope of the velocity- displacement graph
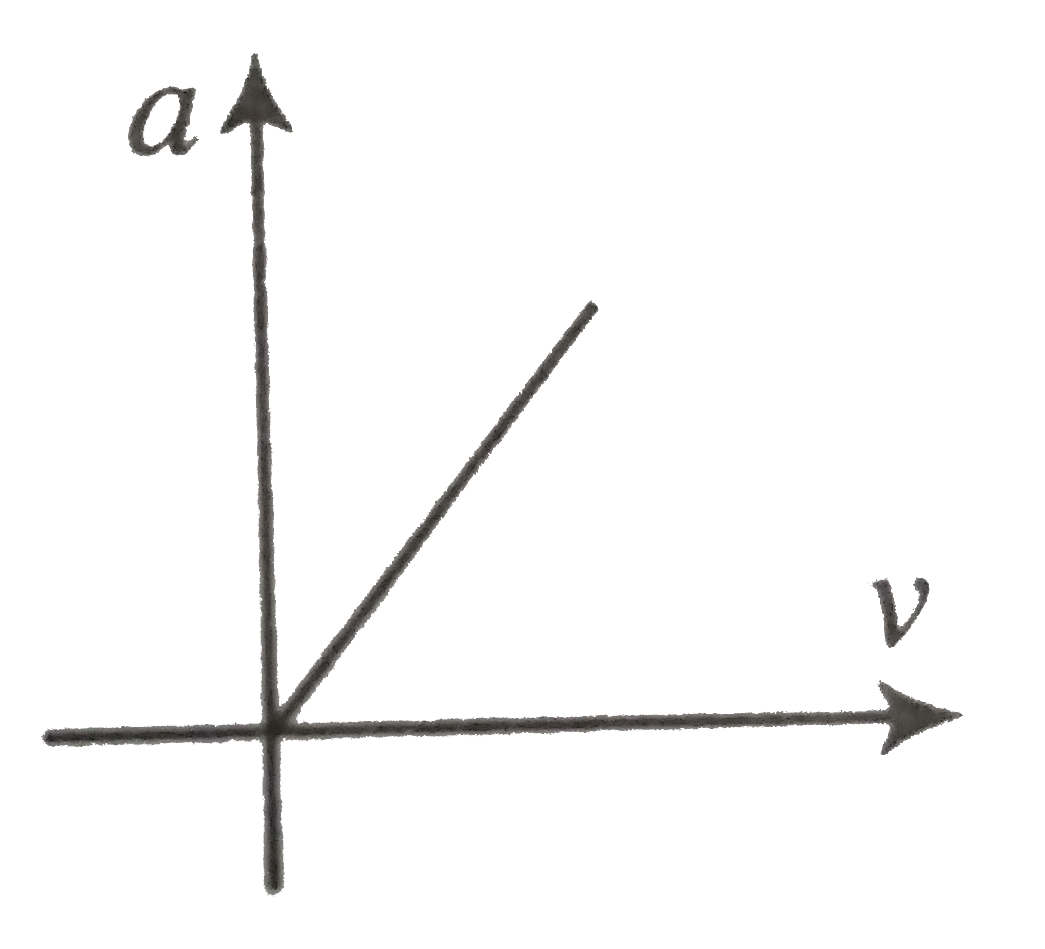 View Solution
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be
 View Solution
View SolutionVelocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?View Solution

