The velocity of centre of mass of the system remains constant, if the total external force acting on the system is.
a. minimum
b. maximum
c. unity
d. zero
The correct Answer is:d
To solve the question, we need to analyze the relationship between the velocity of the center of mass, acceleration, and external forces acting on a system.
1. Understanding the Concept of Center of Mass (COM):
- The center of mass of a system is a point that represents the average position of all the mass in the system. The motion of the center of mass can be described by its velocity.
2. Given Condition:
- The problem states that the velocity of the center of mass remains constant. This is a key point because it implies that there is no change in the velocity over time.
3. Implication of Constant Velocity:
- If the velocity of the center of mass is constant, it means that the acceleration of the center of mass is zero. Mathematically, we can express this as:
aCOM=0
4. Relation Between Acceleration and Force:
- According to Newton's second law, the net external force acting on a system is related to its acceleration:
Fnet=m⋅aCOM
- Since we have established that aCOM=0, we can substitute this into the equation:
Fnet=m⋅0=0
5. Conclusion:
- Therefore, if the velocity of the center of mass remains constant, the net external force acting on the system must be zero. This leads us to conclude that:
Fnet=0
6. Final Answer:
- The total external force acting on the system is zero.
- The center of mass of a system is a point that represents the average position of all the mass in the system. The motion of the center of mass can be described by its velocity.
- The problem states that the velocity of the center of mass remains constant. This is a key point because it implies that there is no change in the velocity over time.
- If the velocity of the center of mass is constant, it means that the acceleration of the center of mass is zero. Mathematically, we can express this as:
aCOM=0
- According to Newton's second law, the net external force acting on a system is related to its acceleration:
Fnet=m⋅aCOM
- Since we have established that aCOM=0, we can substitute this into the equation:
Fnet=m⋅0=0
- Therefore, if the velocity of the center of mass remains constant, the net external force acting on the system must be zero. This leads us to conclude that:
Fnet=0
- The total external force acting on the system is zero.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:TORQUE AND ANGULAR MOMENTUM
Explore 11 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:EQUILIBRIUM OF A RIGID BODY
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:CENTRE OF MASS
Explore 8 Videos
- PRACTICE PAPERSBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPERSExercise:All Questions
Explore 150 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Calculate centre of mass of the system
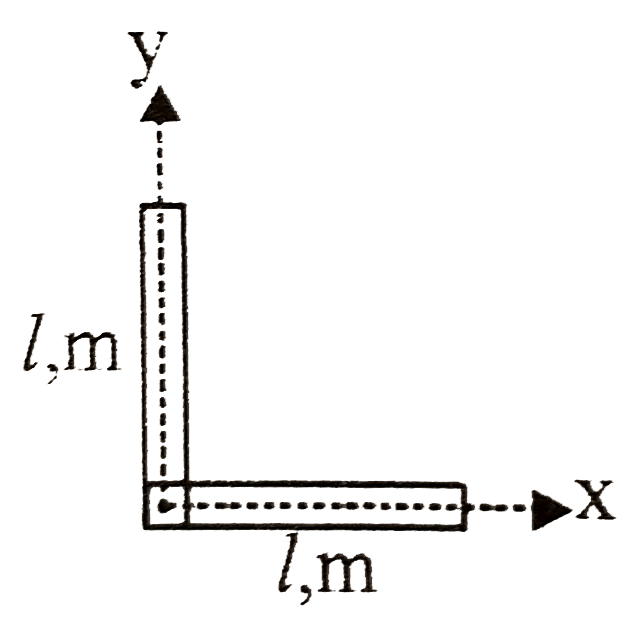
View SolutionIf no external force acts on a system
View SolutionIf no external force acts on a system
View SolutionIf net external force acting on the system is zero then
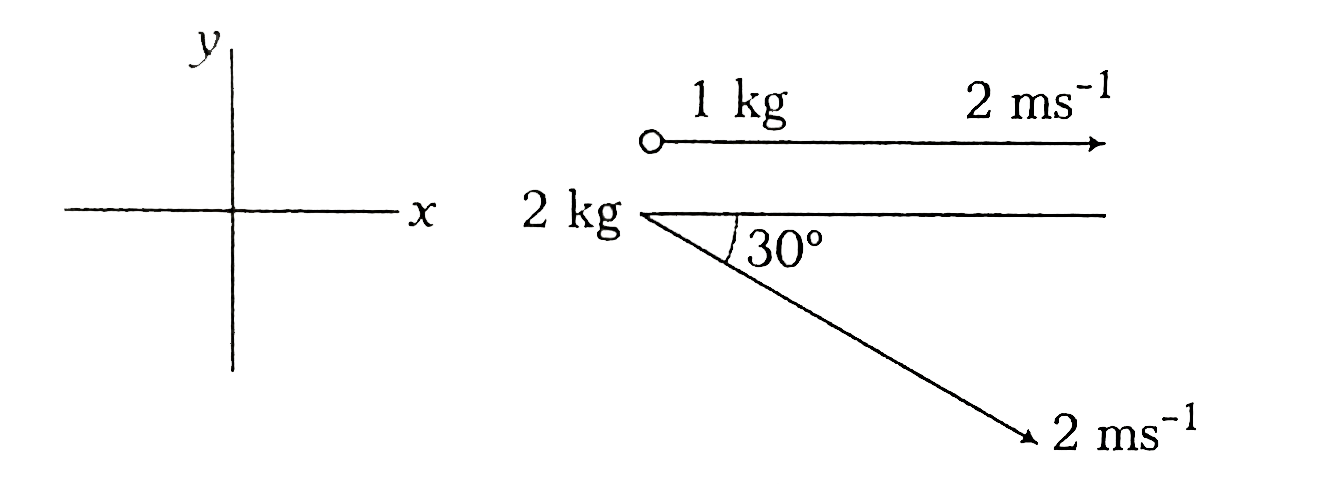
View SolutionFind the velocity of center of mass of the system shown in the figure.
View SolutionA system consists of two particles. At t=0, one particle is at the origin, the other, which has a mass of 0.60kg, is on the y-axis at y=80m. At t=0, the centre of mass of the system is on the y-axis at y=24m and has a velocity given by (6.0m/s)t2ˆj.
(a) Find the total mass of the system.
(b) Find the acceleration of the centre of mass at any time t.
(c) Find the net external force acting on the system at t=3.0s.
View SolutionThe co-ordinates of the centre of mass of the system as shown in figure are
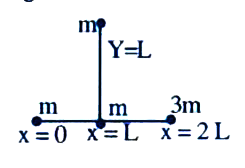
View SolutionThe magnitude of acceleration of centre of mass of the system is

View SolutionIf temperature of the system remains constant during the course of change, the change is
View Solution(a) Show that the velocity of the centre of mass of a moving isolated system remains constant.
View Solution