The correct relation between linear velocity →v and angular velocity →ω of a particle is
→v=→r×→ω
→v=→ω×→r
→ω=→r×→v
→ω=→v×→r
The correct Answer is:b
To find the correct relation between linear velocity →v and angular velocity →ω of a particle, we can follow these steps:
Step 1: Understand the Definitions
- Linear Velocity (→v): This is the rate of change of displacement of a particle. It is a vector quantity that has both magnitude and direction.
- Angular Velocity (→ω): This is the rate of change of angular displacement of a particle. It also is a vector quantity.
Step 2: Relate Linear and Angular Velocity
For a particle moving in a circular path of radius r, the relationship between linear velocity and angular velocity can be expressed mathematically. The linear velocity →v is related to the angular velocity →ω by the formula:
→v=r⋅→ω
where:
- r is the radius of the circular path,
- →ω is the angular velocity vector.
Step 3: Magnitude of the Relation
If we consider the magnitudes of the vectors, we can express the relationship as:
v=r⋅ω
This means that the linear velocity is equal to the radius multiplied by the angular velocity.
Step 4: Conclusion
Thus, the correct relation between linear velocity →v and angular velocity →ω of a particle is:
→v=r⋅→ω
- Linear Velocity (→v): This is the rate of change of displacement of a particle. It is a vector quantity that has both magnitude and direction.
- Angular Velocity (→ω): This is the rate of change of angular displacement of a particle. It also is a vector quantity.
For a particle moving in a circular path of radius r, the relationship between linear velocity and angular velocity can be expressed mathematically. The linear velocity →v is related to the angular velocity →ω by the formula:
→v=r⋅→ω
where:
- r is the radius of the circular path,
- →ω is the angular velocity vector.
If we consider the magnitudes of the vectors, we can express the relationship as:
v=r⋅ω
This means that the linear velocity is equal to the radius multiplied by the angular velocity.
Thus, the correct relation between linear velocity →v and angular velocity →ω of a particle is:
→v=r⋅→ω
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - TORQUE AND ANGULAR MOMENTUM11videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - EQUILIBRIUM OF A RIGID BODY13videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - CENTRE OF MASS8videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The relation between the particles velocity and wave velocity is -
View SolutionShow that the area of the triangle contained between the vector →aand→b is one half of the magnitude of →a×→b
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionGiven vector→A=2ˆI+3ˆj , the angle between →A and y-axis is :
View SolutionThe graph between the angular momentum J and angular velocity ω will be :-
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slippingView SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionChoose the correct option:
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
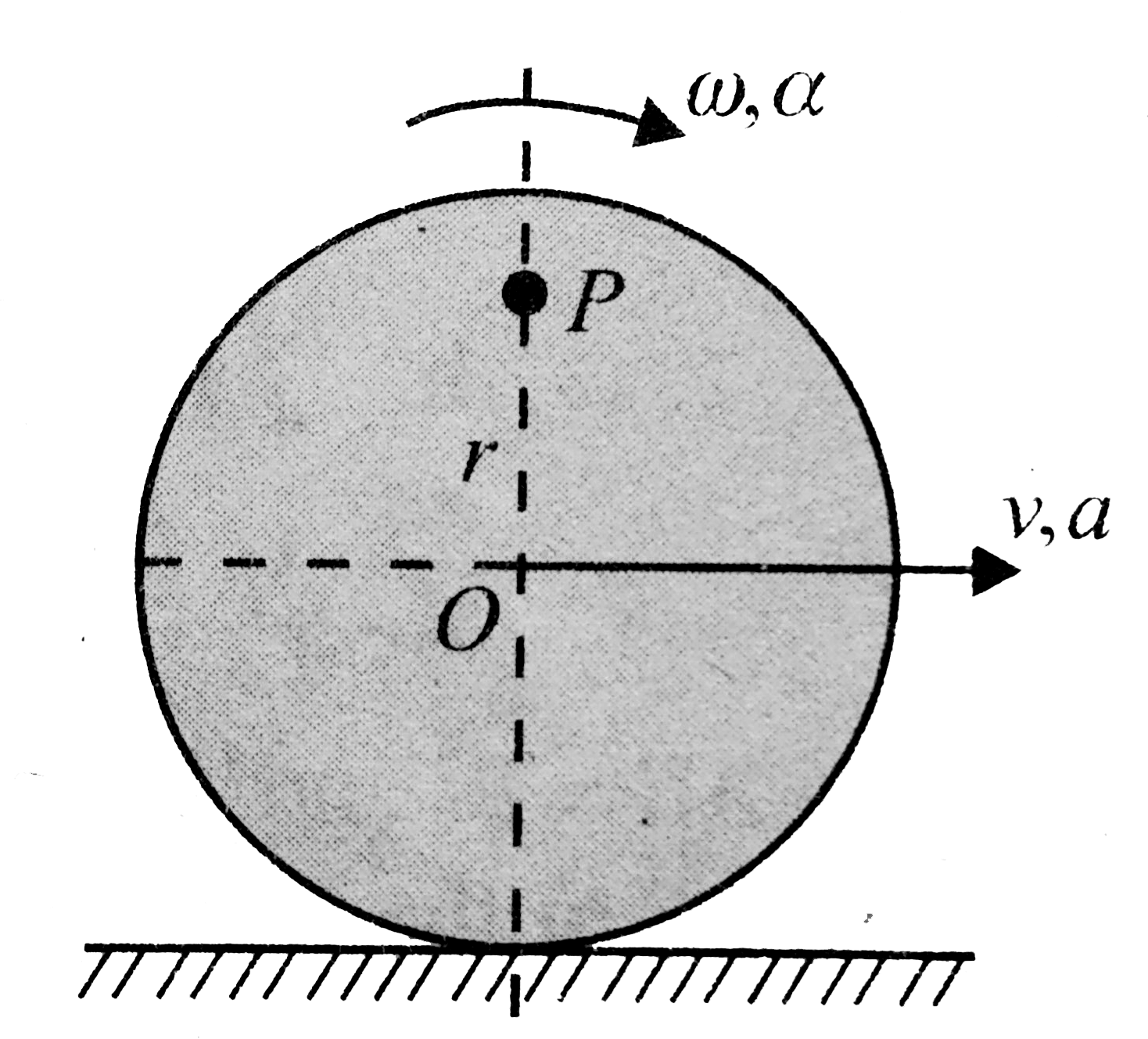 View Solution
View SolutionA disc with linear velocity v and angular velocity ω is placed on rough ground. Suppose a and α be the magnitudes of linear and angular acceleration due to friction.
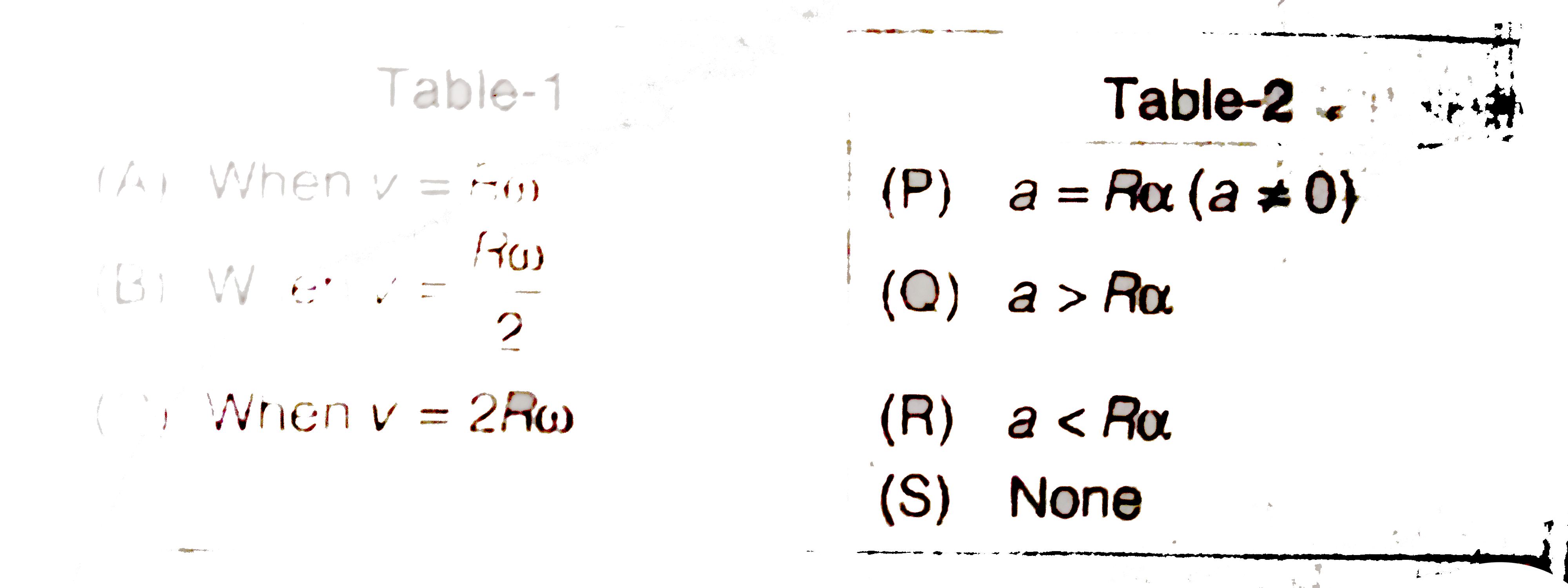
 View Solution
View Solution

