The water level in a vertical glass tube $1.0 m$ long can be adjusted to any position in the tube . A tuning fork vibrating at $660 H z$ is held just over the open top end of the tube . At what positions of the water level will there be resonance . Speed of sound is $330 m / s$ .

Text Solution

Verified by Experts

Resonance corresponds to a pressure antinode at closed end and pressure node at open end. Further , the distance between a pressure node and a pressure antinodes is $λ / 4$ , the condition of resonance would be ,
length of air column
$l = n \frac{λ}{4} = n (\frac{v}{4 f})$
Here , $n = 1, 3, 5, ... .$
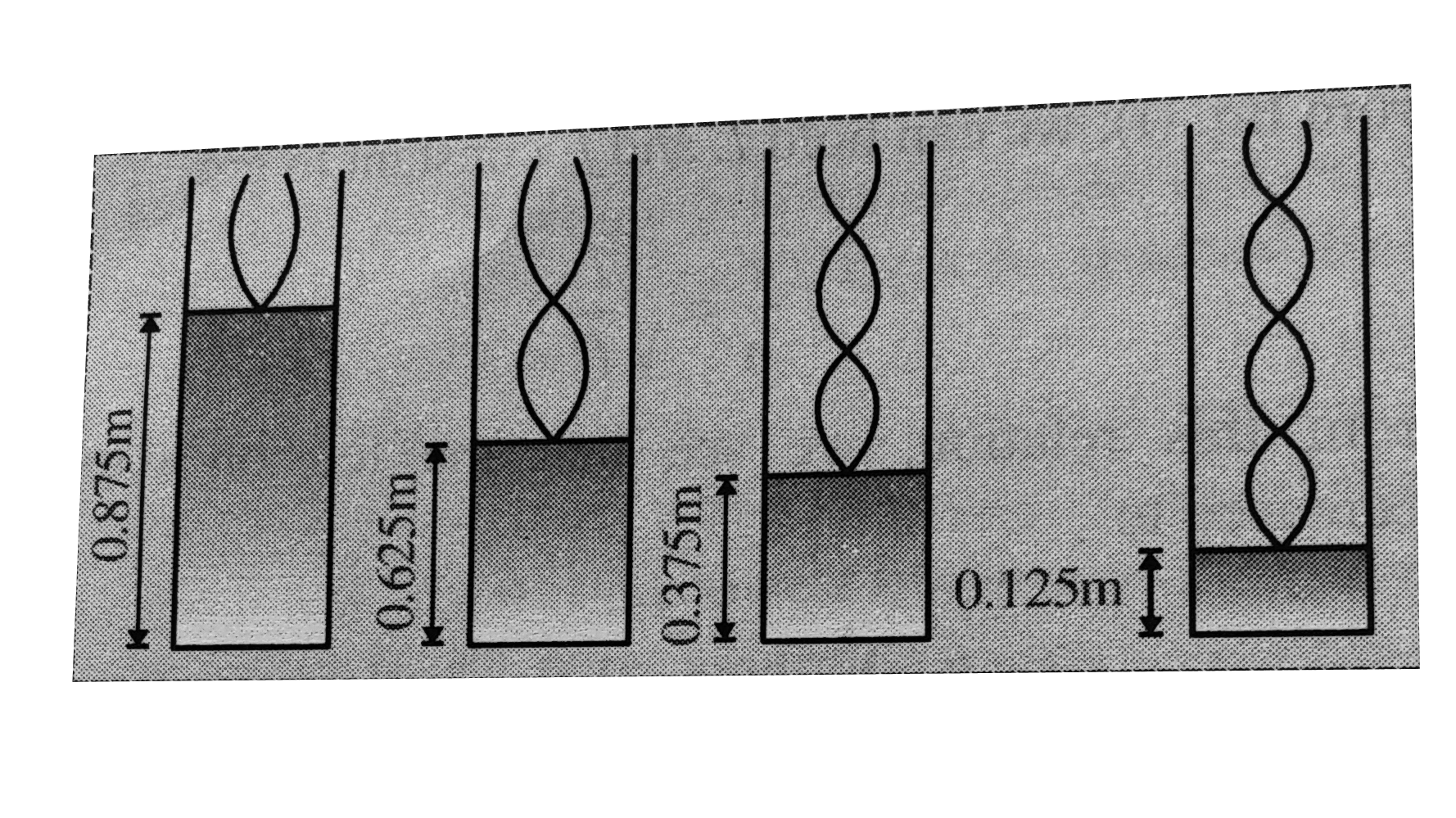
$l_{1} = (1) (\frac{330}{4 \times 660}) = 0.125 m$
and $l_{2} = 3 l_{1} = 0.125 m$
$l_{3} = 5 l_{1} = 0.625 m$
and $l_{4} = 7 l_{1} = 0.875 m$
$l_{3} = 9 l_{1} = 1.125 m$
Since $l_{5} > m$ ( the length of tube), the length of air columns can have the values from $l_{1} \to l_{4}$ only. Therefore , level of water at resonance will be
$(1.0 - 0.125) m = 0.875 m$
$(1.0 - 0.375) m = 0.625 m$
$(1.0 - 0.625) m = 0.375 m$
and $(1.0 - 0.875) m = 0.125 m$
In all the four cases shown in Fig . 7.68, the resonance frequency is $660 H z$ but the first one is the fundamental tone or first harmonic . The second is first overtone or the third harmonic and so on.

A tuning fork of frequency 340 Hz is vibrated just above the tube of 120 cm height. Water is poured slowly in the tube. What is the minimum height of water necessary for the resonance? (speed of sound in the air = 340m/s)
A15 cm
B25 cm
C30 cm
D45 cm
A glass tube $1.5 m$ long and open at both ends, is immersed vertically in a water tank completely. A tuning fork of 660 Hz is vibrated and kept at the upper and of the tube and the tube is gradually raised out of water the total number of resonances heard before the tube comes out of water taking velocity of sound air $330 m / s$ is
A $12$
B $6$
C $8$
D $4$
A glass tube of $1.0 m$ length is filled with water . The water can be drained out slowly at the bottom of the tube . If a vibrating tuning fork of frequency $500 H z$ is brought at the upper end of the tube and the velocity of sound is $300 m / s$ , then the total number of resonances obtained will be
AA. 4
BB. 3
CC. 2
D4. 1