The work done by a force is given by W =→F.→s if W=0 but F≠0 and s≠0 then both →F and →s are
in opposite directions
in te same direction
perpendicular to each other
parallel to each other
The correct Answer is:C
W=→F.→s
=(6ˆi+2ˆj−3ˆk).(2ˆi−3ˆj+xˆk)
But work done = 0
∴0=12−6−3x ∴3x=6 ∴X=2
Topper's Solved these Questions
Similar Questions
The work done by a force →F during a displacement →r is given by →F.→r. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
View SolutionWork done by a force is given by w=→F.→S where →F is the force and →S is the displacement. Show that : Work done is also equal to change in K.E.
View Solution
Knowledge Check
The work done by a force is defined by W=→F⋅→S⋅ It is found that the work done is zero, even if →Fand→s are not equal to zero. From this we conclude that
A→Fand→S are acting in the same directionB→Fand→S are acting in the opposite directionC→Fand→s are acting at right anglesD→Fand→s are acting at an angle of 60∘The linear velocity of a particle on a rotating body is given by →v=→ω×→r where →ω is the angular velocity and →r is the radius vector. What is the value of |v| if →ω=ˆi−2ˆj+2ˆkand→r=4ˆj−3ˆk ?
A√23 unitsB√29 unitsC√35 unitsD√47 unitsA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
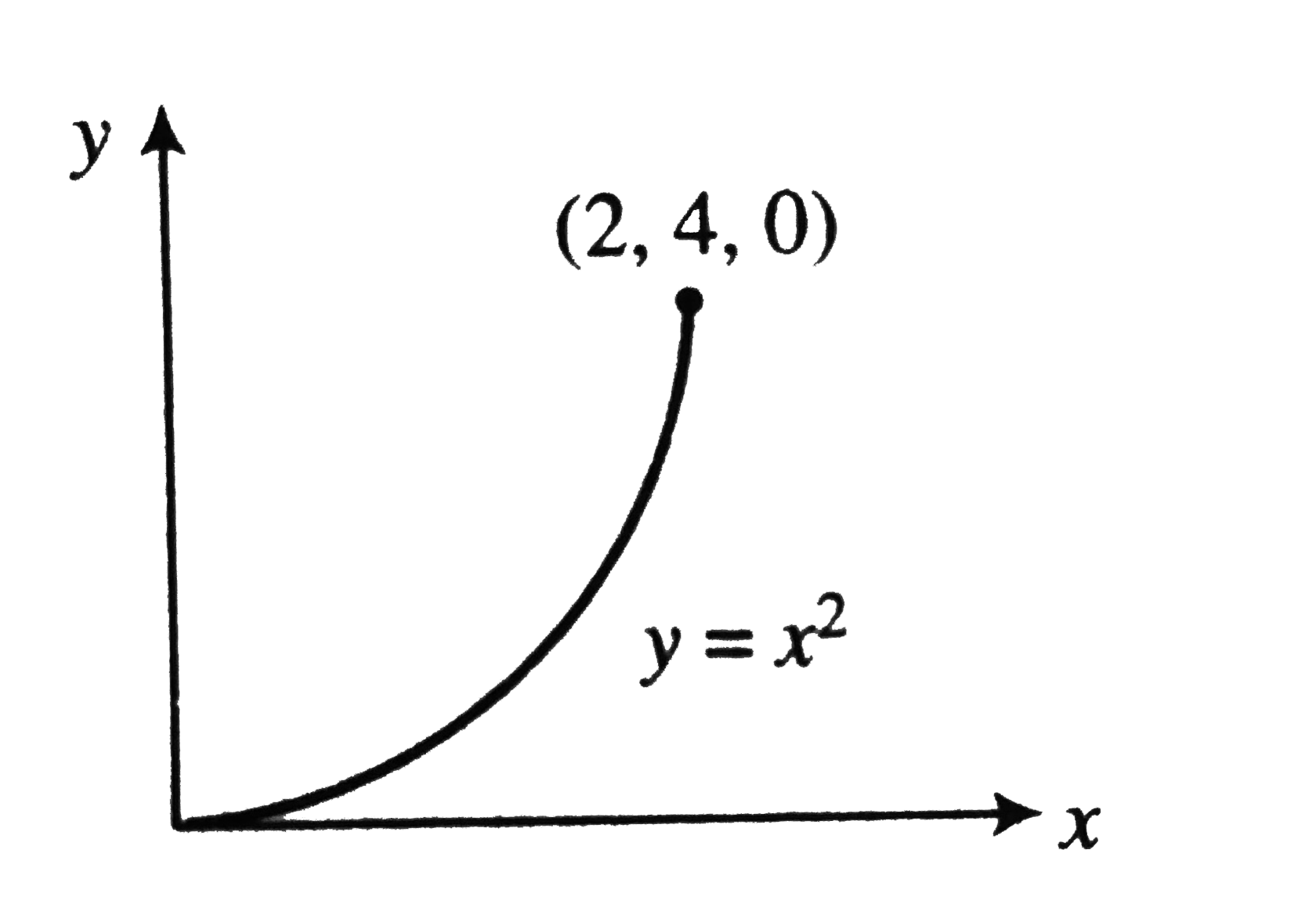 A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
(a) A particle is acted upon by a force →F given by →F=Acosωtˆi+Bˆk and its position vector →r=a[(cos)(ωt)ˆi+sin(ωt)ˆj]+12bt2ˆk. Find the work done on the particle by the force →F from time t=π/2ω to time t=π/ω.
(b) A particle moves under a force →F=xyˆi+y2ˆj and traverses along a path y=4x+1. Find the work done by the force when the particle is displaced from the point P(1, 5) to Q(2, 9).
View SolutionLet →a⋅→b=0,where→aand→b are unit vectors and the unit vector →c is inclined at an angle θ to both →aand→b. If →c=m→a+n→b+p(→a×→b),(m,n,p∈R), then a.−π4≤θ≤π4 b. π4≤θ≤3π4 c. 0≤θ≤π4 d. 0≤θ≤3π4
View SolutionA force →F=ˆi+5ˆj+7ˆk acts on a particle and displaces it throught →s=6ˆI+9ˆk. Calculate the work done if the force is in newton and displacement in metre.
(ii) Find the work done by force →F=2ˆi−3ˆj+ˆk when its point of application moves from the point A(1,2,-3) to the point B (2,0, -5).
View SolutionA 0.25 kg puck is initially stationary on an ice surface with negligible friction. At time t = 0, a horizontal force begins to move the puck. The force is given by →F=(12.0−3.00t2)ˆi, with →F in newtons and t in seconds, and it acts until its magnitude is zero. (a) What is the magnitude of the impulse on the puck from the force between t= 0.750 s and t = 1.25 s? (b) What is the change in momentum of the puck between t=0 and the instant at which F=0?
View SolutionGiven →F=(xy2)ˆi+(x2y)ˆjN. The work done by →F when a particle is taken along the semicircular path OAB where the coordinates of B are (4,0) is
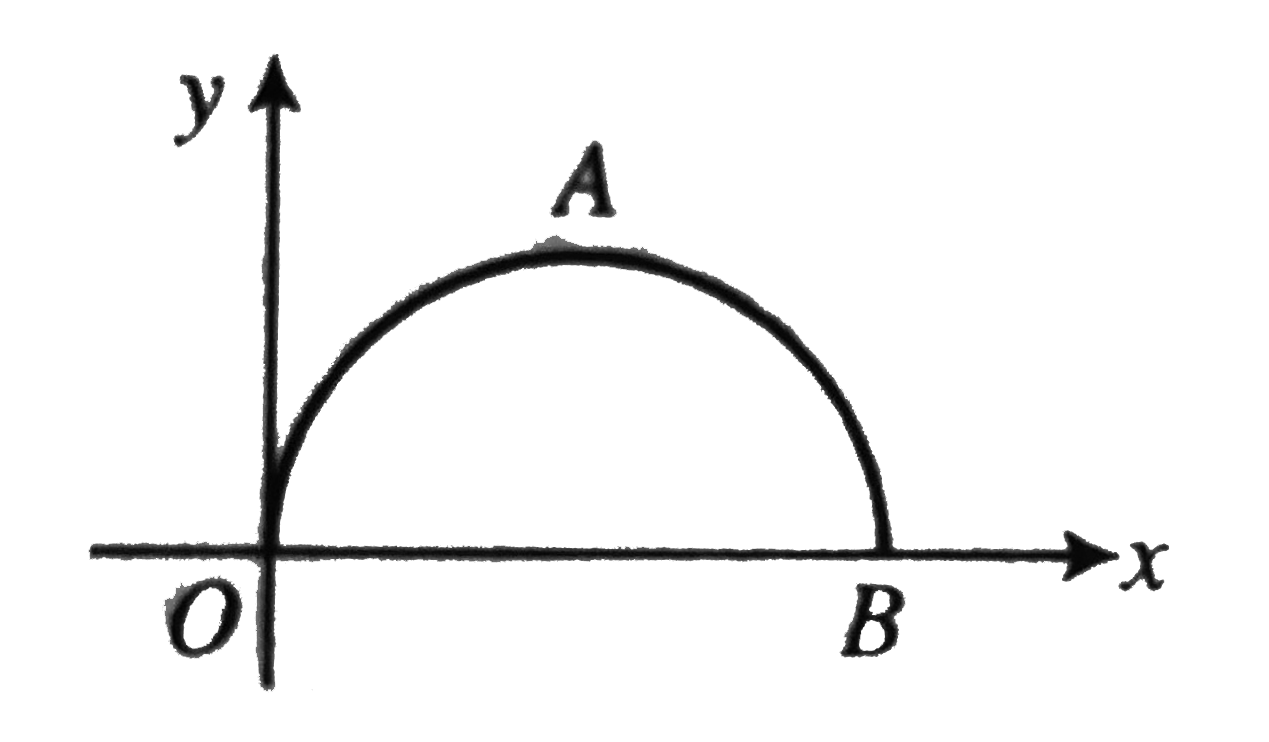
View Solution
