A 0.25 kg puck is initially stationary on an ice surface with negligible friction. At time t = 0, a horizontal force begins to move the puck. The force is given by →F=(12.0−3.00t2)ˆi, with →F in newtons and t in seconds, and it acts until its magnitude is zero. (a) What is the magnitude of the impulse on the puck from the force between t= 0.750 s and t = 1.25 s? (b) What is the change in momentum of the puck between t=0 and the instant at which F=0?
The correct Answer is:(a)4.47 N.s ; (b)(16 N.s) ˆi ;
To solve the given problem, we will break it down into two parts: (a) calculating the magnitude of the impulse on the puck from the force between t = 0.750 s and t = 1.250 s, and (b) determining the change in momentum of the puck between t = 0 and the instant at which the force becomes zero.
Part (a): Magnitude of Impulse
1. Identify the Force Function:
The force acting on the puck is given by:
→F=(12.0−3.00t2)^i (in newtons)
2. Impulse Calculation:
Impulse (J) is defined as the integral of force over time:
J=∫t2t1→Fdt
Here, t1=0.750 s and t2=1.250 s.
3. Set Up the Integral:
Substitute the force function into the integral:
J=∫1.2500.750(12.0−3.00t2)dt
4. Calculate the Integral:
- First, integrate 12.0:
∫12.0dt=12.0t
- Then, integrate −3.00t2:
∫−3.00t2dt=−t3
- Thus, the integral becomes:
J=(12.0t−t3)1.2500.750
5. Evaluate the Integral:
- Calculate at t=1.250:
12.0(1.250)−(1.250)3=15.0−1.953125=13.046875
- Calculate at t=0.750:
12.0(0.750)−(0.750)3=9.0−0.421875=8.578125
- Now, subtract:
J=13.046875−8.578125=4.46875 Ns
6. Final Result for Part (a):
The magnitude of the impulse is approximately:
J≈4.47 Ns
Part (b): Change in Momentum
1. Determine When the Force Becomes Zero:
Set the force function to zero:
12.0−3.00t2=0⟹3.00t2=12.0⟹t2=4⟹t=2.0 s
2. Calculate the Change in Momentum:
The change in momentum (Δp) is equal to the impulse over the entire time from t=0 to t=2.0:
Δp=∫2.00→Fdt=∫2.00(12.0−3.00t2)dt
3. Set Up the Integral:
Δp=(12.0t−t3)2.00
4. Evaluate the Integral:
- Calculate at t=2.0:
12.0(2.0)−(2.0)3=24.0−8.0=16.0
- Calculate at t=0:
12.0(0)−(0)3=0
- Now, subtract:
Δp=16.0−0=16.0 Ns
5. Final Result for Part (b):
The change in momentum of the puck is:
Δp=16.0 Ns
Summary of Results
- (a) The magnitude of the impulse on the puck between t=0.750 s and t=1.250 s is approximately 4.47 Ns.
- (b) The change in momentum of the puck between t=0 and the instant at which F=0 is 16.0 Ns.
The force acting on the puck is given by:
→F=(12.0−3.00t2)^i (in newtons)
Impulse (J) is defined as the integral of force over time:
J=∫t2t1→Fdt
Here, t1=0.750 s and t2=1.250 s.
Substitute the force function into the integral:
J=∫1.2500.750(12.0−3.00t2)dt
- First, integrate 12.0:
∫12.0dt=12.0t
- Then, integrate −3.00t2:
∫−3.00t2dt=−t3
- Thus, the integral becomes:
J=(12.0t−t3)1.2500.750
- Calculate at t=1.250:
12.0(1.250)−(1.250)3=15.0−1.953125=13.046875
- Calculate at t=0.750:
12.0(0.750)−(0.750)3=9.0−0.421875=8.578125
- Now, subtract:
J=13.046875−8.578125=4.46875 Ns
The magnitude of the impulse is approximately:
J≈4.47 Ns
Set the force function to zero:
12.0−3.00t2=0⟹3.00t2=12.0⟹t2=4⟹t=2.0 s
The change in momentum (Δp) is equal to the impulse over the entire time from t=0 to t=2.0:
Δp=∫2.00→Fdt=∫2.00(12.0−3.00t2)dt
Δp=(12.0t−t3)2.00
- Calculate at t=2.0:
12.0(2.0)−(2.0)3=24.0−8.0=16.0
- Calculate at t=0:
12.0(0)−(0)3=0
- Now, subtract:
Δp=16.0−0=16.0 Ns
The change in momentum of the puck is:
Δp=16.0 Ns
- (a) The magnitude of the impulse on the puck between t=0.750 s and t=1.250 s is approximately 4.47 Ns.
- (b) The change in momentum of the puck between t=0 and the instant at which F=0 is 16.0 Ns.
Topper's Solved these Questions
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )
47 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)
5 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionA point mass of 1 kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1 kg mass reverses its direction and moves with a speed of 2 m/s. Which of the following statements are correct for the system of these two masses?
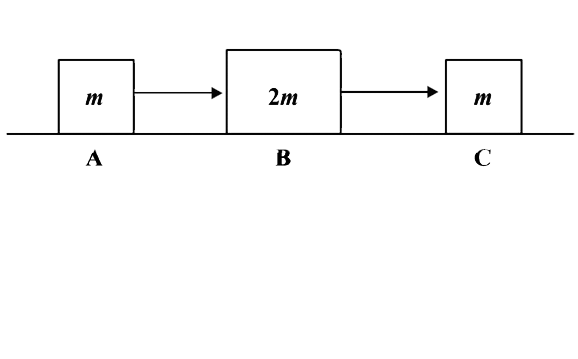
View SolutionThere object A,B and C are kept is a straing line a fritionlas horizental surface . These have masses have increase on 2m and m repectively . The object A move toward B with a speed 9 m//s and makes as electic collision with a there after B makes complately inclesis with C . All motion over on the same strangth line . Find the first speed of the object C
View SolutionP and Q are two capacitors with capacitance 10μF and 20μF respectively which are connected in series with a battery of value 12V. Find the ratio between the charges and P and Q.
View SolutionWhen two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
View SolutionAt t = 0 aparticle of mass m start moving from rest due to a force vecF = F_(0) sin (omega t)hati :
View SolutionA small puck is sliding to the right with momentum →P1 on a horizontal, frictionless surface, as shown in figure. A force is applied to the puck for a short time and its momentum afterward is →Pf. Which lettered arrow shows the direction of the impulse that was delovered to the puck ?
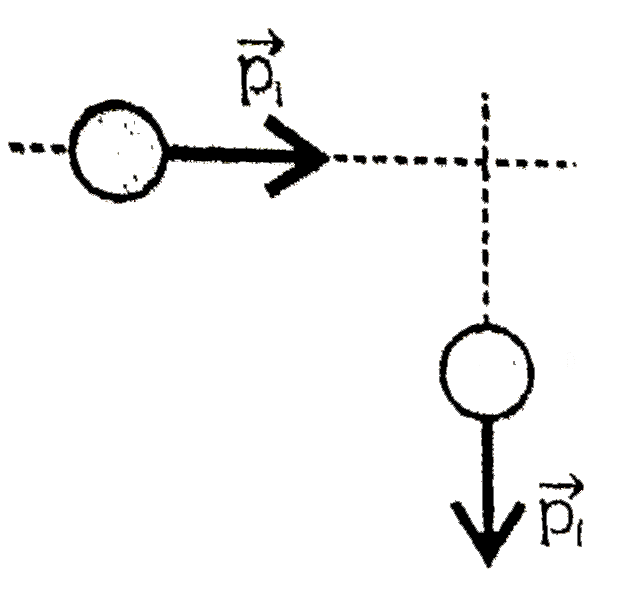
View SolutionTwo pucks are initially moving along a frictionless surface as shown in the diagram. The pucks have mass m1<m2 and begin with equal magnitude of momentum. A constant force →F is applied to each puck direactly to the right for the same amount of non−zero time. After the pushes are complete, what is the relationship for the size of the moments of pucks (p1 and p2) ?

View SolutionA force →F=6t2ˆi+4tˆj is acting on a particle of mass 3 kg then what will be velocity of particle at t=3 second and if at t=0, particle is at rest:-
View SolutionA body of mass 1 kg is acted upon by a force vecF=2sin3pithati+3cos3pithatj find its position t=1 sec if at t=0 it is at rest at origin.
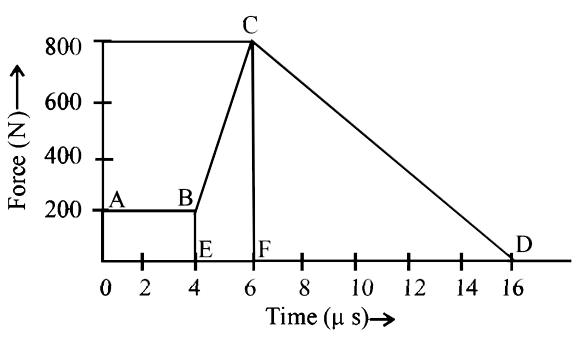
View SolutionThe magnitude of force (in Newtons) acting on a body varies with time (in micro second) as shown in the figure. The magnitude of total impulse of the force on the body from t = 4μs to t = 16μs is –
View Solution3 किग्रा का एक पिंड विरामावस्था में है । यदि इस पर एक बल →F=6t2ˆi+4tˆj न्यूटन आरोपित किया जाये , तो t=3 सेकंड पर पिंड का वेग होगा -
View SolutionDuring hockey practice, two pucks are sliding across the ice in the same direction. At one instant, a 0.18-kg puck is moving at 16 m/s while the other puck has a mass of 0.14 kg and a speed of 3.8 m/s. What is the velocity of the center of mass of the two pucks?
View Solutionएक बल →F=6t2ˆi+4tˆj, 3 किग्रा द्रव्यमान के कण पर कार्यरत है, तो t = 3 सेकण्ड पर कण का वेग क्या होगा यदि t = 0 पर कण स्थिरावस्था में है?
View SolutionThe magnitude of the force (in newtons) acting on a body varies with time t (in micro seconds) as shown in the fig AB, BC and CD are straight line segments. The magnitude of the total impulse of the force on the body from t=4μs to t=16μs is ….Ns
View Solution
