The work done to move a unit charge along an equipotential from P to Q
must be defined as −Q∫P→E.→dl
is zero
can have a non-zero value
both (a) and (b)are correct
The correct Answer is:D
To solve the problem of finding the work done to move a unit charge along an equipotential surface from point P to point Q, we can follow these steps:
Step 1: Understand the Concept of Equipotential Surfaces
Equipotential surfaces are surfaces where the electric potential is the same at every point. This means that if you move a charge along an equipotential surface, there is no change in electric potential energy.
Hint: Remember that electric potential (V) is constant along an equipotential surface.
Step 2: Define Work Done in Moving a Charge
The work done (W) in moving a charge (Q) from point P to point Q in an electric field is given by the formula:
W=Q(VQ−VP)
where VQ is the potential at point Q and VP is the potential at point P.
Hint: Work done depends on the change in potential energy, which is determined by the difference in electric potential.
Step 3: Apply the Concept to the Given Problem
Since points P and Q are on the same equipotential surface, we have:
VP=VQ
Thus, substituting this into the work done formula gives:
W=Q(VQ−VP)=Q(0)=0
Hint: Since the potential difference is zero, the work done will also be zero.
Step 4: Conclusion
For a unit charge (Q = 1), the work done to move it from point P to point Q along an equipotential surface is:
W=0
Final Answer
The work done to move a unit charge along an equipotential from P to Q is 0.
---
Equipotential surfaces are surfaces where the electric potential is the same at every point. This means that if you move a charge along an equipotential surface, there is no change in electric potential energy.
The work done (W) in moving a charge (Q) from point P to point Q in an electric field is given by the formula:
W=Q(VQ−VP)
where VQ is the potential at point Q and VP is the potential at point P.
Since points P and Q are on the same equipotential surface, we have:
VP=VQ
Thus, substituting this into the work done formula gives:
W=Q(VQ−VP)=Q(0)=0
For a unit charge (Q = 1), the work done to move it from point P to point Q along an equipotential surface is:
W=0
The work done to move a unit charge along an equipotential from P to Q is 0.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS3videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
Similar Questions
The work done to move a charge along an equipotential from A to B
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionSTATEMENT-1 : Work done to move a charge on the surface of metal solid charged cylinder is always zero.
and
STATEMENT-2 : Work done to move a charge on an equipotential surface is zero.View SolutionWork done per unit time
View SolutionDefine the emf (E) of a cell and the potential difference (V) across a resistor (R) in terms of the work done in moving a unit charge. State the relation between these two works and the work it charge through a cell connected across the resistor. Take the internal resistance of the cell as r. Hence, obtain expression for the current i in the circuit.
View SolutionCharge q2 is at the centre of a circular path with radius r. work done in carrying charge q1 once around this equipotential path , would be
View SolutionThe work done in slowly moving an electron of charge e and mass m from A to B along semicircular path (as shown in the figure ) in vertical plane in the field of charge Q is .
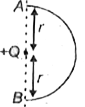 View Solution
View SolutionA uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .View Solution
.View SolutionThe work done in moving an electric charge q in an electric field does not depend upon
View SolutionIn the figure given below , the zero potential is taken at infinity. The work done in moving a unit charge from A to B is , Where VArightarrow potential at point A, VBrightarrow potential at point B
 View Solution
View Solution
