There are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are exerting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
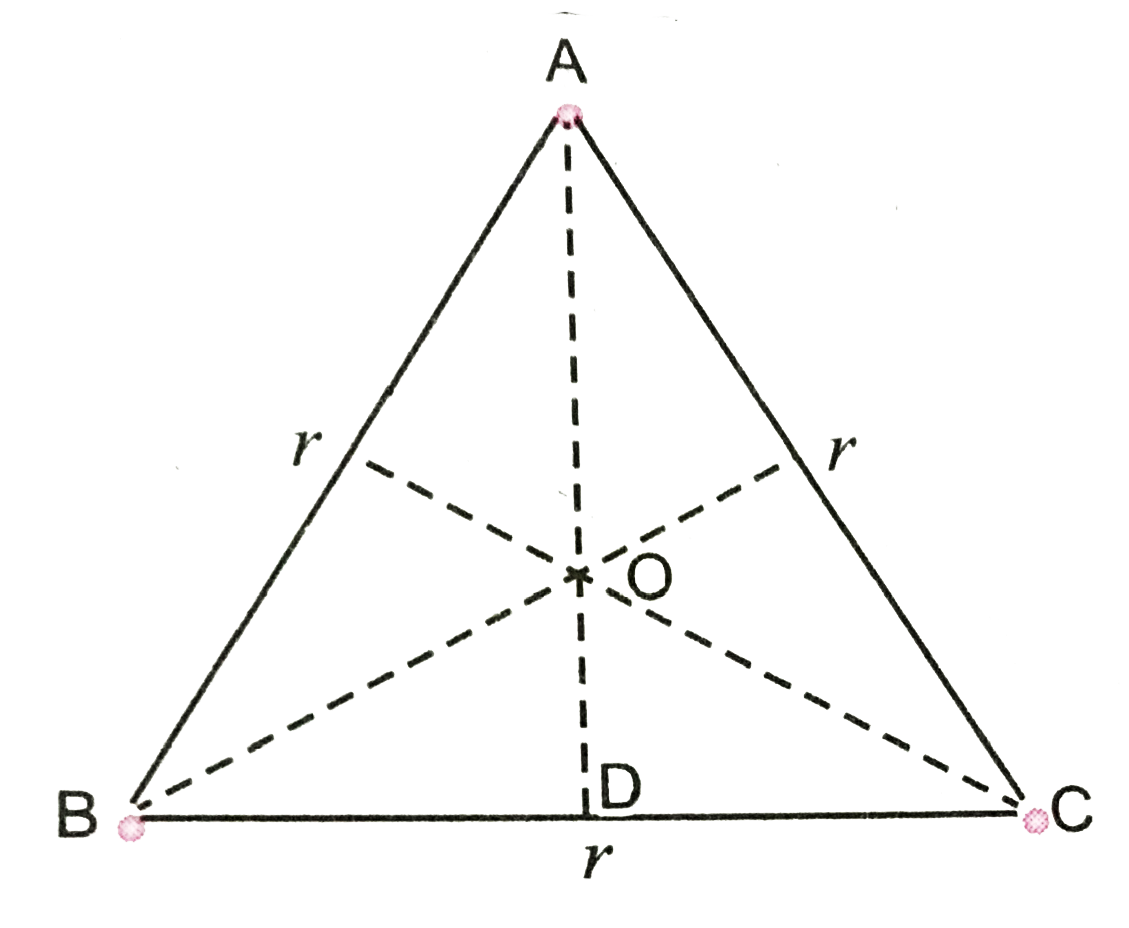
Answer the following questions :
At what speed must they move if they all revolve under the influence of one another's gravitation in a circular orbit circumsribing the triangle still preserving the equilateral triangle
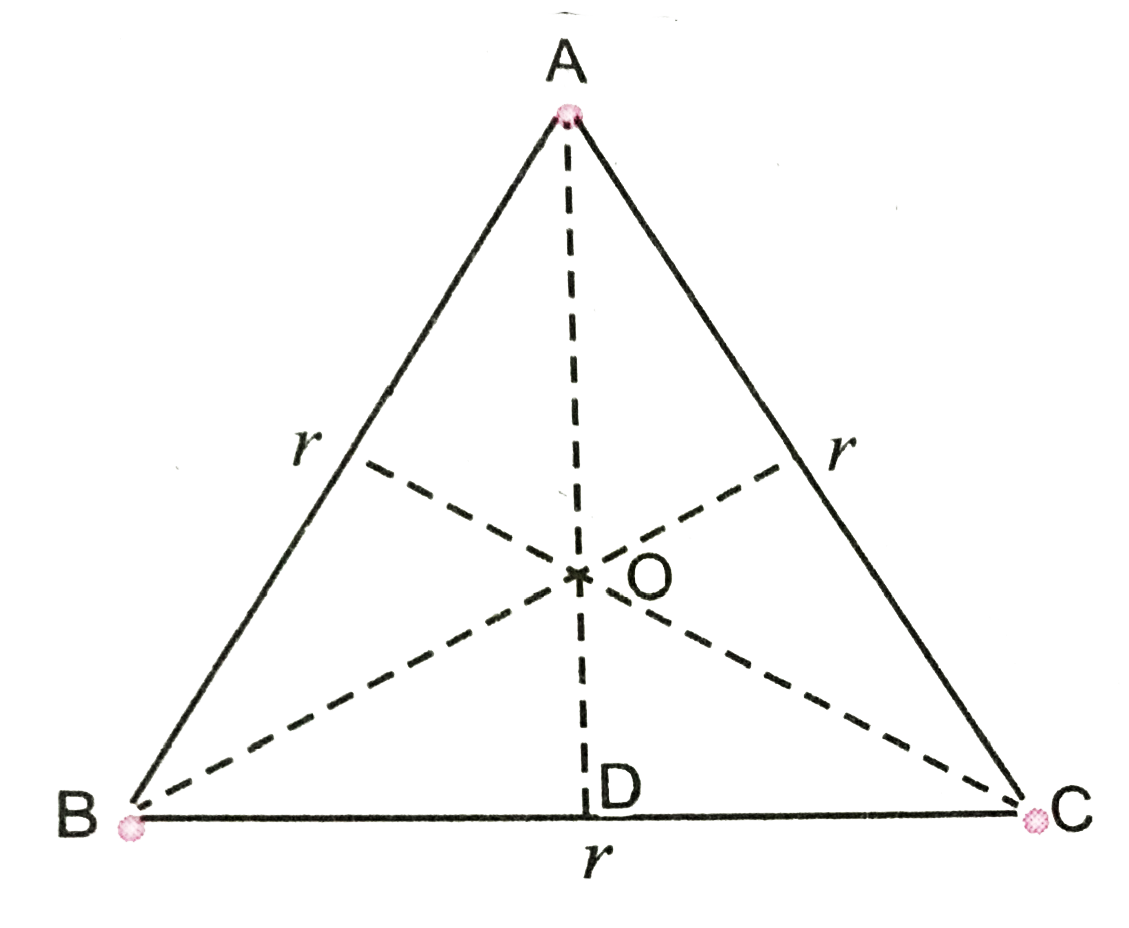
Refer to Fig. (APC).1, force of attracting on body at C due to body at A is
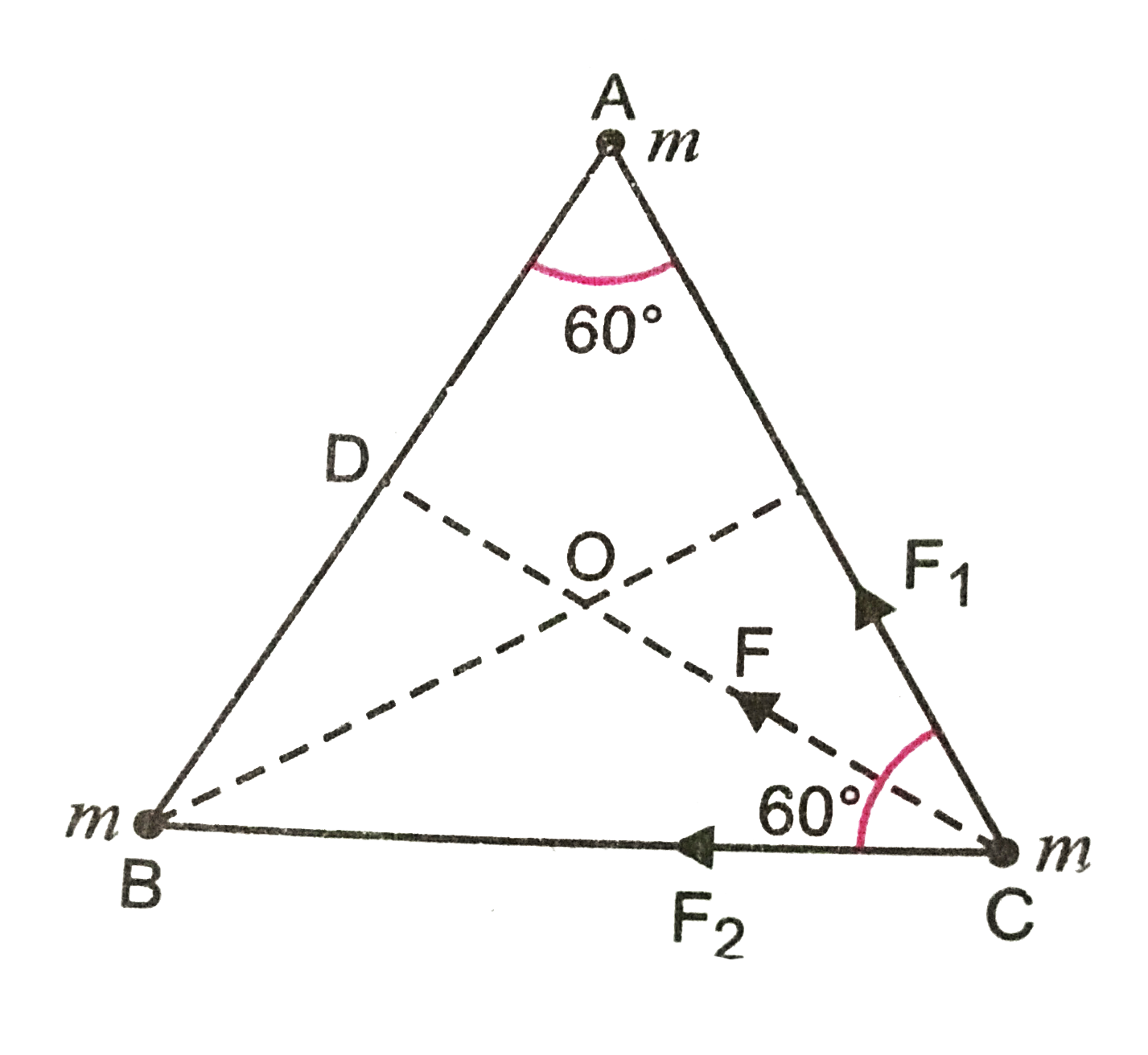
F1=Gm×mr2along CA
Force of attracting on body at C due to body at B is
F2=Gm×mr2 along CB
These force −→F1 and −→F2 are inclined at an angle 60∘, so the resultant force on body at C is
F=√F21+F22+2F1F2cos60∘
=√F21+F21+2F1F2×1/2
=√3F1=√3Gm2r2 along CD
Here, CO=23CD=23×ACsin60∘
=23×r√32=r√3.
When each body is decribing a circular orbit with centre of orbit at O, the force F provides the required centripetel force. The radius of the circular orbit is OC(=r/√3). If υ is the speed of the body in circular orbit, then
mυ2r/√3=√3Gm2r2 or υ=√Gmr
∴υ=√(6.67×10−11)×21=1.155×10−5ms−1
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - NCERT
21 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - ADDITIONAL EXERCISES
4 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - LONG ANSWER QUESTIONS
11 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View Solution
Knowledge Check
There are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are experting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
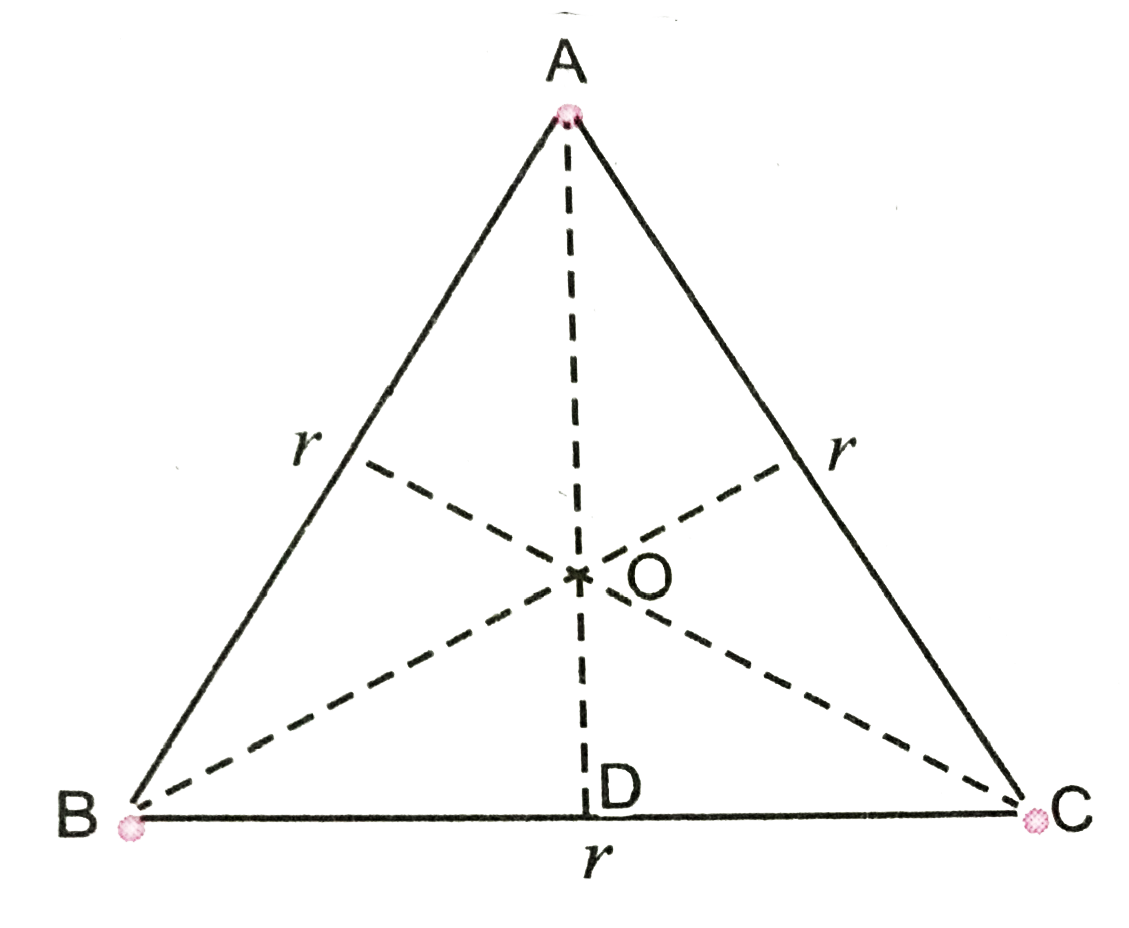
Answer the following questions :
Work done in taking one body far away from the other two bodies isA−Gm2rBGm2rC2Gm2rD−2Gm2rThere are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are experting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
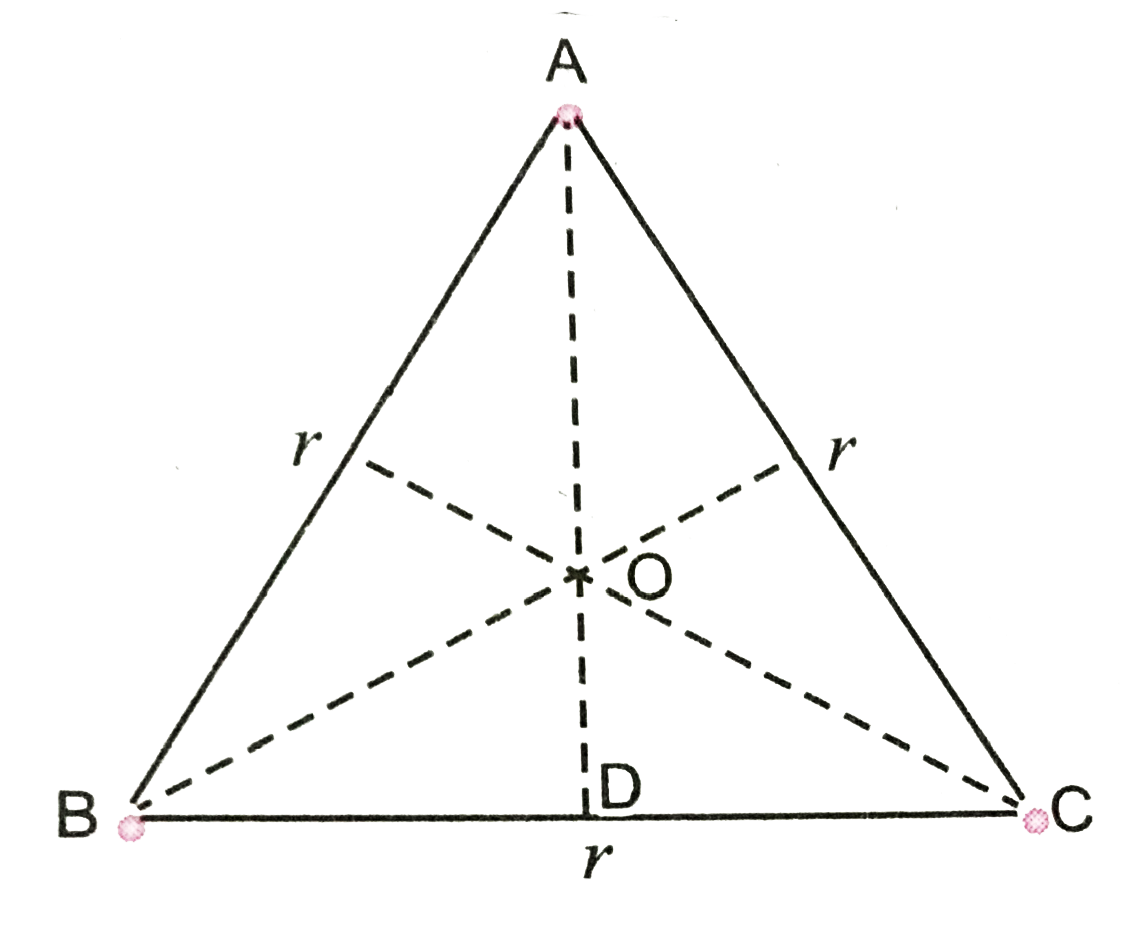
Answer the following questions :
The magnitude of the gravitational force on one body due to other two bodies isAGm2r2B2Gm2r2C3Gm2r2D√3Gm2r2There are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are experting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
Answer the following questions :
Magnitude of gravitational field at the mid point D of arm BC of triangle ABC isAGm2r2BGm3r2C3Gmr2D4Gm3r2
If two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionThree identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View SolutionThree particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution
