There are two blocks of masses and is placed on on a table which is rotating with an angular velocity about the vertical axis . The coefficent of friction between the block is and between and table is if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed

(a)
If there is no sliding between therefore
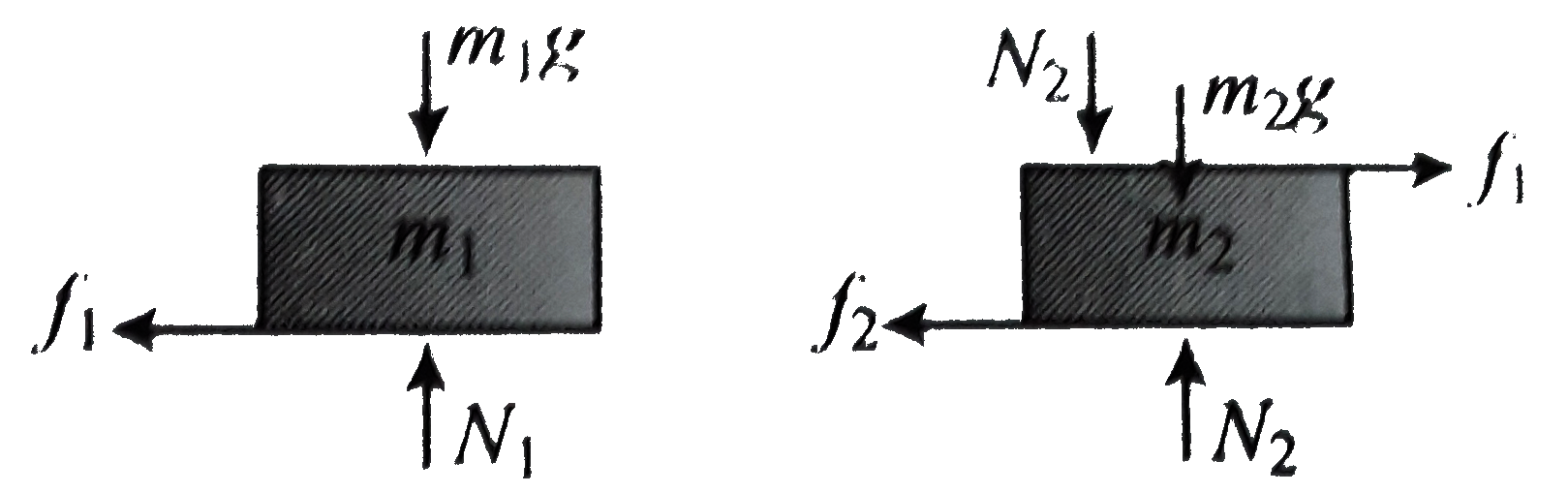
If there is no sliding between and ground
As hence maximum angular velocity will be
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View Solution
Knowledge Check
Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
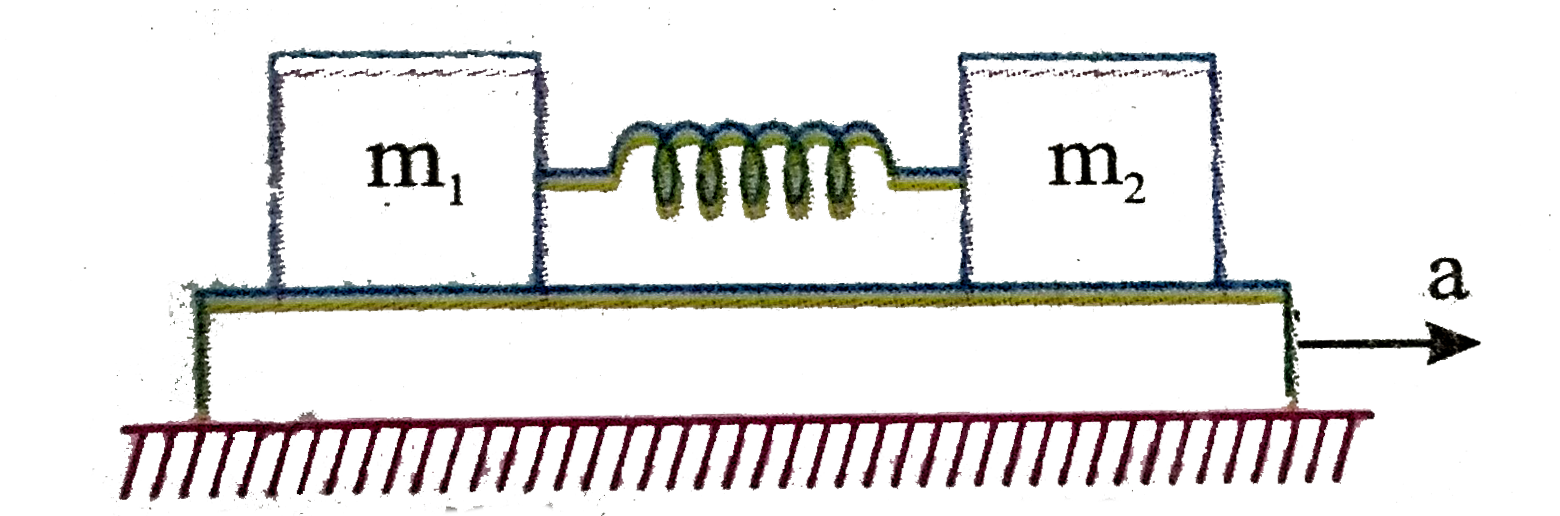 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.Two blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest
 A4/3kgB8/9kgC1kgD8/5kg
A4/3kgB8/9kgC1kgD8/5kgTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is
 Azero in all casesBzero only if m1=m2Cnon zero only if a>2μgDnon zero only if a>μg
Azero in all casesBzero only if m1=m2Cnon zero only if a>2μgDnon zero only if a>μg
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
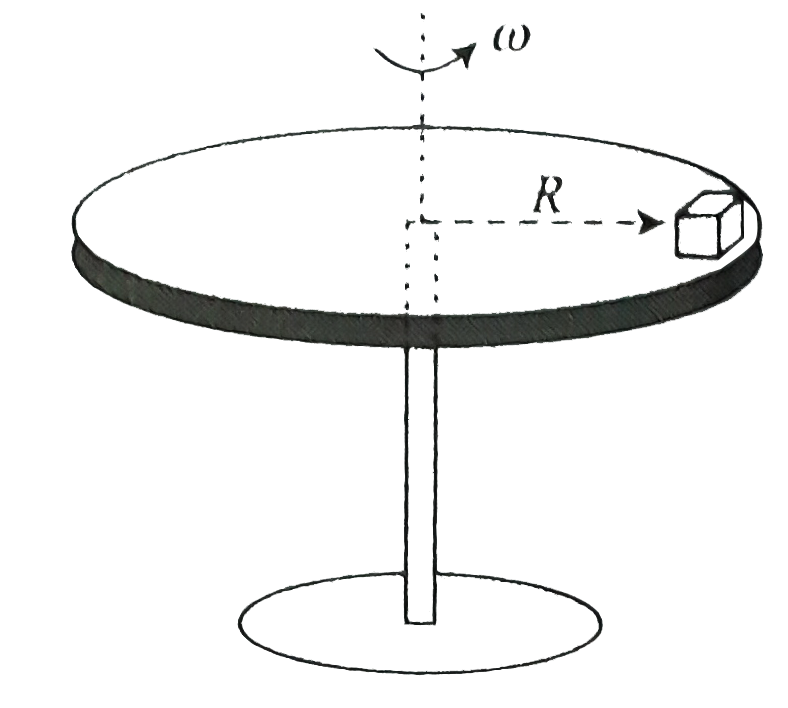
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
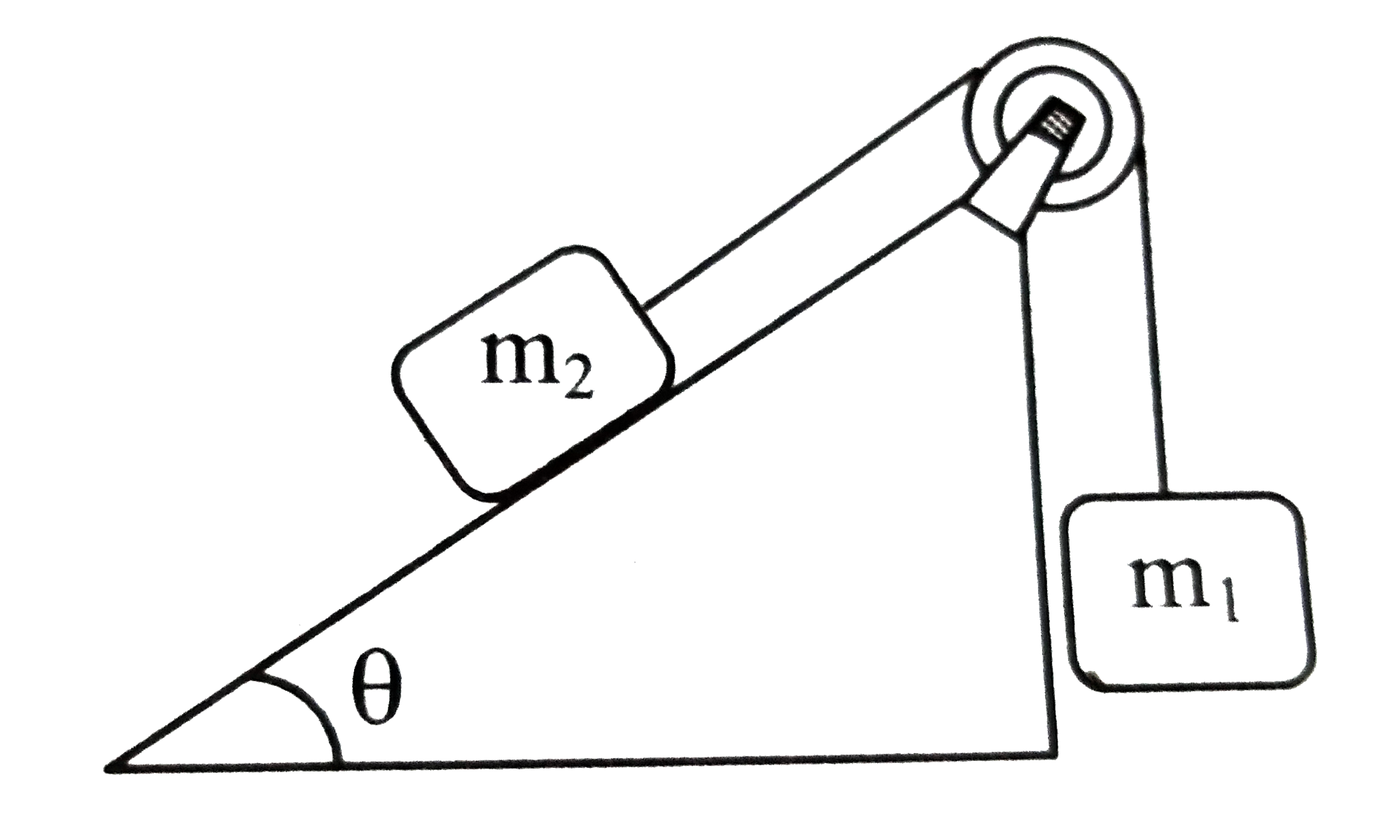
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View Solution
