There exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
(0,1,2)m
(0,−π2/2,−2)m
(2,π2/2,2)m
(0,π2/2,2)m
The correct Answer is:d
To solve the problem step by step, we will analyze the motion of the charged particle in the presence of uniform electric and magnetic fields.
Step 1: Identify the given parameters
- Charge (q) = 1 C
- Mass (m) = 1 kg
- Velocity (v) = 1 m/s (along the x-axis)
- Magnetic field (B) = 1 T (along the y-axis)
- Electric field (E) = 1 V/m (along the y-axis)
- Initial position = (0, 0, 0) at time t=0
Step 2: Determine the force acting on the particle
The total force F acting on the charged particle can be calculated using the Lorentz force equation:
F=q(E+v×B)
Here, since the electric field E and magnetic field B are both in the y-direction, we need to calculate v×B:
- The velocity vector →v=(1,0,0) m/s
- The magnetic field vector →B=(0,1,0) T
Calculating the cross product:
v×B=∣∣
∣
∣∣^i^j^k100010∣∣
∣
∣∣=(0,0,1)
Thus, the magnetic force is:
FB=q(v×B)=1⋅(0,0,1)=(0,0,1) N
The electric force is:
FE=qE=1⋅(0,1,0)=(0,1,0) N
Adding these forces gives:
F=FE+FB=(0,1,0)+(0,0,1)=(0,1,1) N
Step 3: Calculate acceleration
Using Newton's second law F=ma:
a=Fm=(0,1,1)1=(0,1,1) m/s2
Step 4: Determine the motion in the y and z directions
The particle moves linearly in the y and z directions due to the electric and magnetic forces. The equations of motion for the y and z coordinates can be derived from the kinematic equations.
For the y-coordinate:
y(t)=uyt+12ayt2
Here, uy=0 (initial velocity in the y-direction) and ay=1:
y(t)=0⋅t+12⋅1⋅t2=12t2
For the z-coordinate:
z(t)=uzt+12azt2
Here, uz=0 (initial velocity in the z-direction) and az=1:
z(t)=0⋅t+12⋅1⋅t2=12t2
Step 5: Calculate the coordinates at t=π
Substituting t=π:
- For y-coordinate:
y(π)=12π2
- For z-coordinate:
z(π)=12π2
Step 6: Determine the x-coordinate
Since the particle is moving in a circular path in the x-y plane due to the magnetic field, we need to find the x-coordinate. The time period T for the circular motion is given by:
T=2πmqB=2π⋅11⋅1=2π seconds
At t=π, the particle completes half of the circular path, which means the x-coordinate will be 0 (it will be at the y-axis).
Final coordinates
Thus, the coordinates of the particle at t=π seconds are:
(x,y,z)=(0,12π2,12π2)
Answer
The coordinates of the particle at time π seconds are:
(0,π22,π22)
- Charge (q) = 1 C
- Mass (m) = 1 kg
- Velocity (v) = 1 m/s (along the x-axis)
- Magnetic field (B) = 1 T (along the y-axis)
- Electric field (E) = 1 V/m (along the y-axis)
- Initial position = (0, 0, 0) at time t=0
The total force F acting on the charged particle can be calculated using the Lorentz force equation:
F=q(E+v×B)
Here, since the electric field E and magnetic field B are both in the y-direction, we need to calculate v×B:
- The velocity vector →v=(1,0,0) m/s
- The magnetic field vector →B=(0,1,0) T
v×B=∣∣
∣
∣∣^i^j^k100010∣∣
∣
∣∣=(0,0,1)
FB=q(v×B)=1⋅(0,0,1)=(0,0,1) N
FE=qE=1⋅(0,1,0)=(0,1,0) N
F=FE+FB=(0,1,0)+(0,0,1)=(0,1,1) N
Using Newton's second law F=ma:
a=Fm=(0,1,1)1=(0,1,1) m/s2
The particle moves linearly in the y and z directions due to the electric and magnetic forces. The equations of motion for the y and z coordinates can be derived from the kinematic equations.
y(t)=uyt+12ayt2
Here, uy=0 (initial velocity in the y-direction) and ay=1:
y(t)=0⋅t+12⋅1⋅t2=12t2
z(t)=uzt+12azt2
Here, uz=0 (initial velocity in the z-direction) and az=1:
z(t)=0⋅t+12⋅1⋅t2=12t2
Substituting t=π:
- For y-coordinate:
y(π)=12π2
- For z-coordinate:
z(π)=12π2
Since the particle is moving in a circular path in the x-y plane due to the magnetic field, we need to find the x-coordinate. The time period T for the circular motion is given by:
T=2πmqB=2π⋅11⋅1=2π seconds
At t=π, the particle completes half of the circular path, which means the x-coordinate will be 0 (it will be at the y-axis).
Thus, the coordinates of the particle at t=π seconds are:
(x,y,z)=(0,12π2,12π2)
The coordinates of the particle at time π seconds are:
(0,π22,π22)
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionThe magnetic field exists along negative x-axis and electric field exists along positive x-axis. A charged particle moves with a velocity inclined at an angle (θ) with vertical in (x-y) plane. What will be the correct diagram of the helical path?
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionUniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.Thec∞rd∈ateY_(n) of the particle when it crosses the y-axis for the nth time is:
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
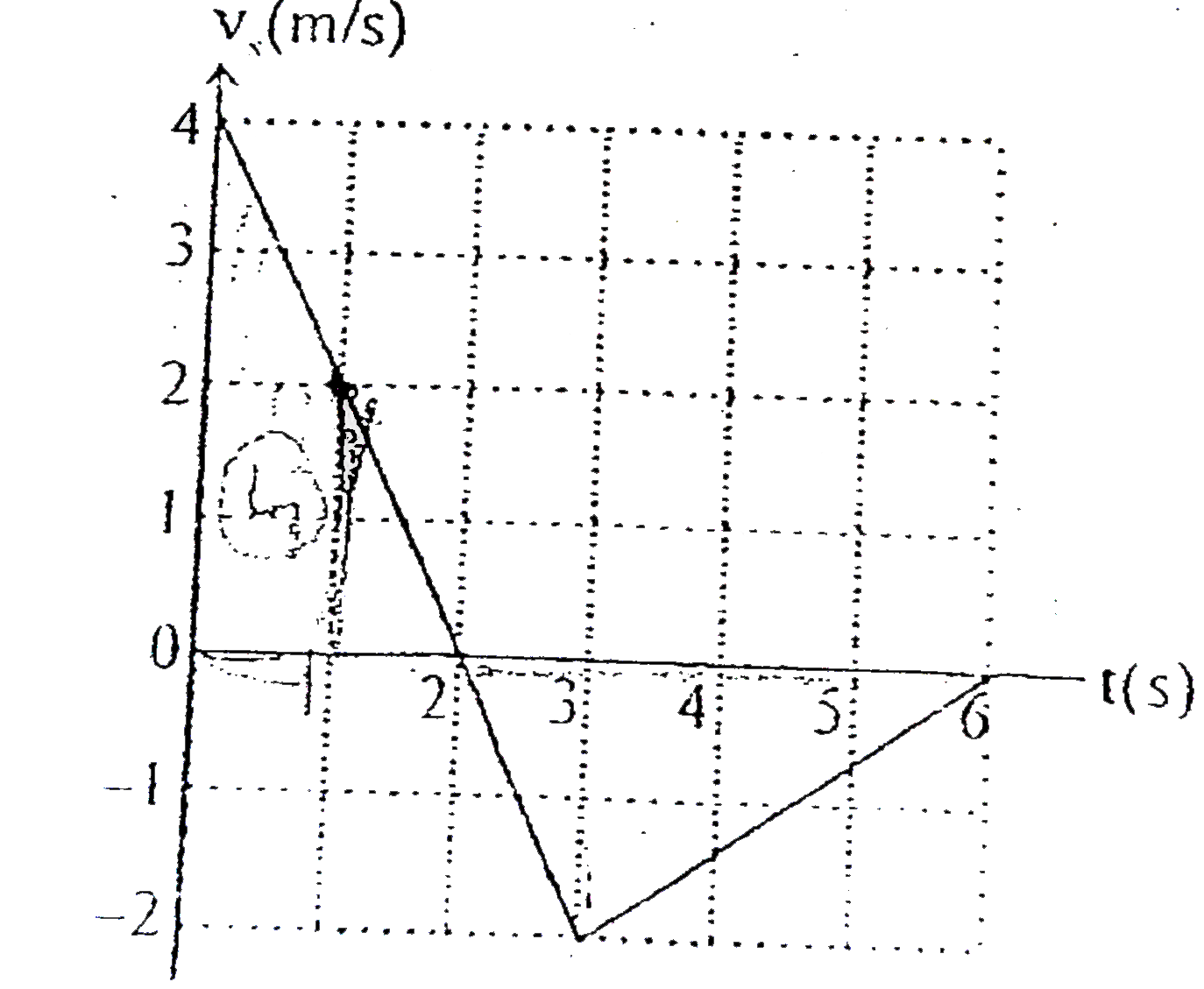
View SolutionA particle of mass 2 kg charge 1 mC is projected vertially with velocity k10ms−1. There is as uniform horizontal electric field of 104N/C, then
View SolutionA uniform magnetic field B and electric field E exist along y and negative z axis respectively. Under the influence of these field a charge particle moves along OA undeflected. If electric field is switched off, find the pitch of helical trajectory in which the particle will move.

View Solution
