There in fairly long solenoid whose length is l and radial of its cross section is b. This solenoid is connected to a battery of emf V and a, resistor of resistance R in series with it along with a key which is initially open. A thin wire ring of radius a and resistance r is kept inside the solenoid in such a manner that axis of solenoid coincides with axis of ring. Assume thay there in no self-inductance at the ring. Find the value of radical force per unit length of the ring as a function of time if key is closed at t=0. What would be the maximum value of this radical force per unit length?
When current grows in solenoid, then flux linked with the ring also changes which induces emf in the ring and it causes flow of current in it. This ring is placed in magnetic feild of solenoid which is acting perpendicular to the plane of ring. When current flows in the ring, then it experiences radical force everywhere on its length.
We can write self-inductance L of the solenoid as follows:
L=μ0n2b2l ...(i)
Current as a function of time in the solenoid can be written as follows:
i=VR(1−e−tRL)
Magnetic field inside the solenoid can be written as
B=μ0ni
⇒B=μ0nVR(1−e−tRL) ...(ii)
Magnetic flux linked with the ring can be written as follows:
ϕ=B(πa2)=μ0nVπa2R(1−e−tRL)
emf induced can be be written as follows:
ε=∣∣∣dϕdt∣∣∣=μ0nVπa2R(RLe−tRL)
ε=μ0nVπa2Le−tRL
We know that r is resistance of ring and hence current flowing in the ring can be written as follows:
I=εr=μ0nVπa2rLe−tRL ...(iii)
If we select a segment of length dl on the circumference of ring then radial force acting on this segment can be written as follows:
dF = IdlB
Hence radial force acting per unit length of the ring can be written as
dFdt=IB
⇒dFdt=(μ0nVπa2rLe−tRL)[μ0nVR(1−e−tRL)]
We can also substitute value of self-inductance L from equation (i) to get the following:
⇒dFdl=(μ0nVπa2rμ0πn2b2le−tRL)[μ0nVR(1−e−tRL)]
⇒dFdl=μ0V2a2rb2lR[e−tRL(1−e−tRL)]
Above expression represents radial force acting on the ring per unit length as a function of time.
To calculate maximum value of this force, we need to differentiate it and put it equal to zero. After calculation we get that above force per unit length is maximum when e−tR/L=1/2. Substituting this above relation we get maximum value of this force per unit length as follows:
⇒(dFdl)maximum=μ0V2a24rb2lR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT TEXTBOOK EXERCISE)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT ADDITIONAL EXERCISE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l, its cross-sectional radius , to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the the radial force acting per unit length of the ring.
View SolutionA thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l, its cross-sectional radius , to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the the radial force acting per unit length of the ring.
View Solution
Knowledge Check
A ring of area A and resistance R is placed on the axis of a solenoid. The mutual inductance between them is M. When the current in the solenoid changes at the rate of I, the magnetic moment of the ring is
AARMIBAI/RMCMRI/ADAMI/RConsider a metal ring kept on top of a fixed solenoid (say on a carboard) The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on then
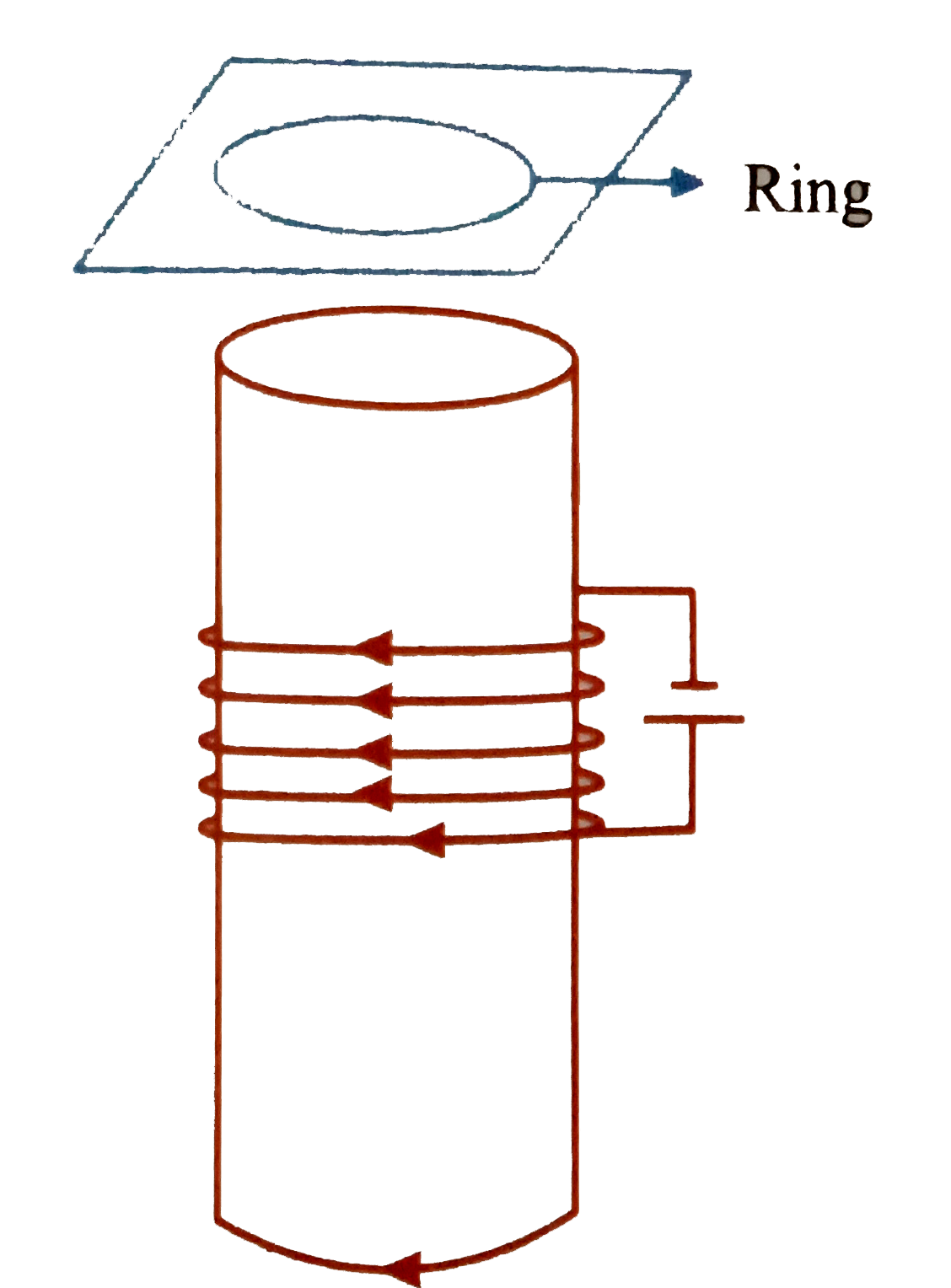 AThe metal ring is attractedBThe metal ring is jumped upCNo change in magnetic flux through the ring when switch is suddenly closedDCan not be decided.
AThe metal ring is attractedBThe metal ring is jumped upCNo change in magnetic flux through the ring when switch is suddenly closedDCan not be decided.The diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
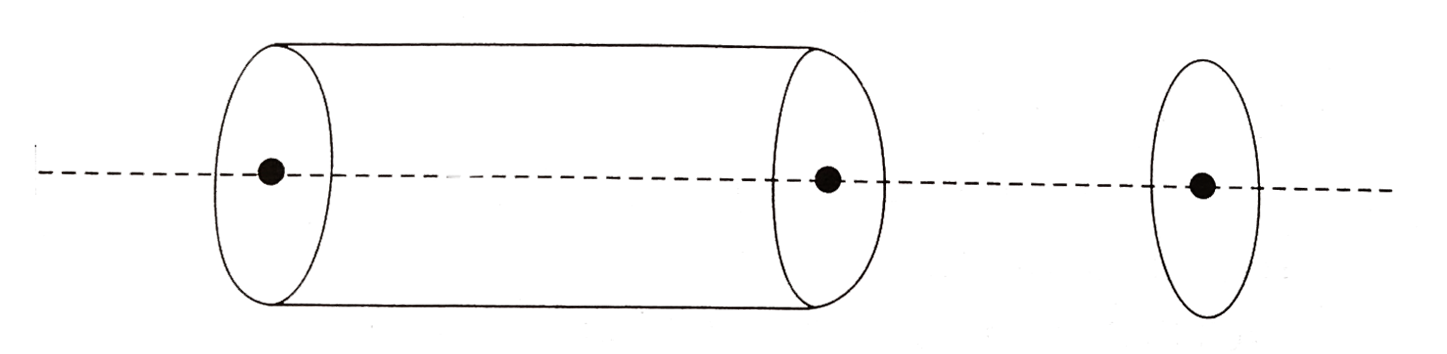 A(2M+L)I0RBMI0RC(2M−L)I0RD(M+L)I0R
A(2M+L)I0RBMI0RC(2M−L)I0RD(M+L)I0R
shows a horizontal solenoid connected to a battery and a switch. A coper ring is placed on a frictionless track, the axis of the ring being along the axis of the solenoid. As the switch is closed, the ring will

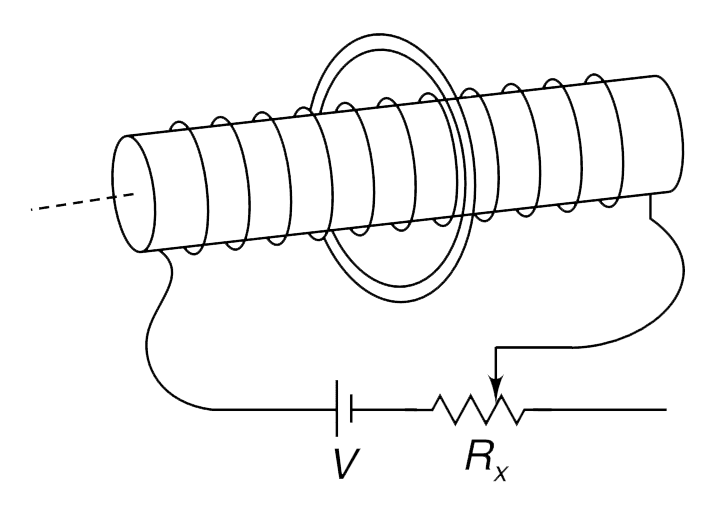
View SolutionA long narrow solenoid of radius a has n turns per unit length and resistance of the wire wrapped on it is R. The solenoid is connected to a battery of emf V through a variable resistance Rx. There is a conducting ring of radius 2a held fixed around the solenoid with its axis coinciding with that of the solenoid. The relaxation time of free electrons inside the material of the conducting ring at given temperature is τ and specific charge of an electron is α. The variable resistance Rx is changed linearly with time from zero to R in an interval Δt. Calculate the drift speed of the free electrons in the ring during this interval. [Neglect inductance]
View SolutionA wire of fixed length is wound on a solenoid of length l and radius r, its self inductance is found to be L. If same wire is wound on a solenoid of length l3 and radius r3, then self inductance will be
View SolutionFind the inductance of a solenoid of length l whose winding is made of copper wire of mass m. The winding resistance is equal to R. The solenoid diameter is considerably less than its length.
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is

View Solution
