There is a cylindrical vessel of radius 10 cm and a cylindrical glass piece of radius 5 cm and height 10 cm is kept inside it. Volume of water 950πcm3 is poured into it. Bottom of the glass piece is seen with paraxial rays. What will be the apparent depth of bottom of glass cylinder? Index of refraction of glass is 3/2 and that of water is 4/3.
Let h be the total height of the water from bottom as shown in figure.
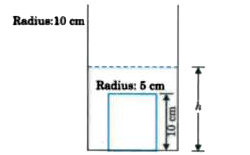
Total volume of water=950πcm3
π(10)2h−π(5)2×10=950π
⇒ 100πh−250π=950π
⇒ h=12cm
Height of layer of water above the cylindrical glass piece is =12−10=2cm. We can use the following relation to calculate apparent depth :
apparent depth=real depthμ
Apparent depth of the bottom of glass piece
=24/3+103/2=32+203=9+406=496cm.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Very Short Answer Questions)82videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)22videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (Exemplar Problems Subjective Questions) (Very Short Answer Type Questions)11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
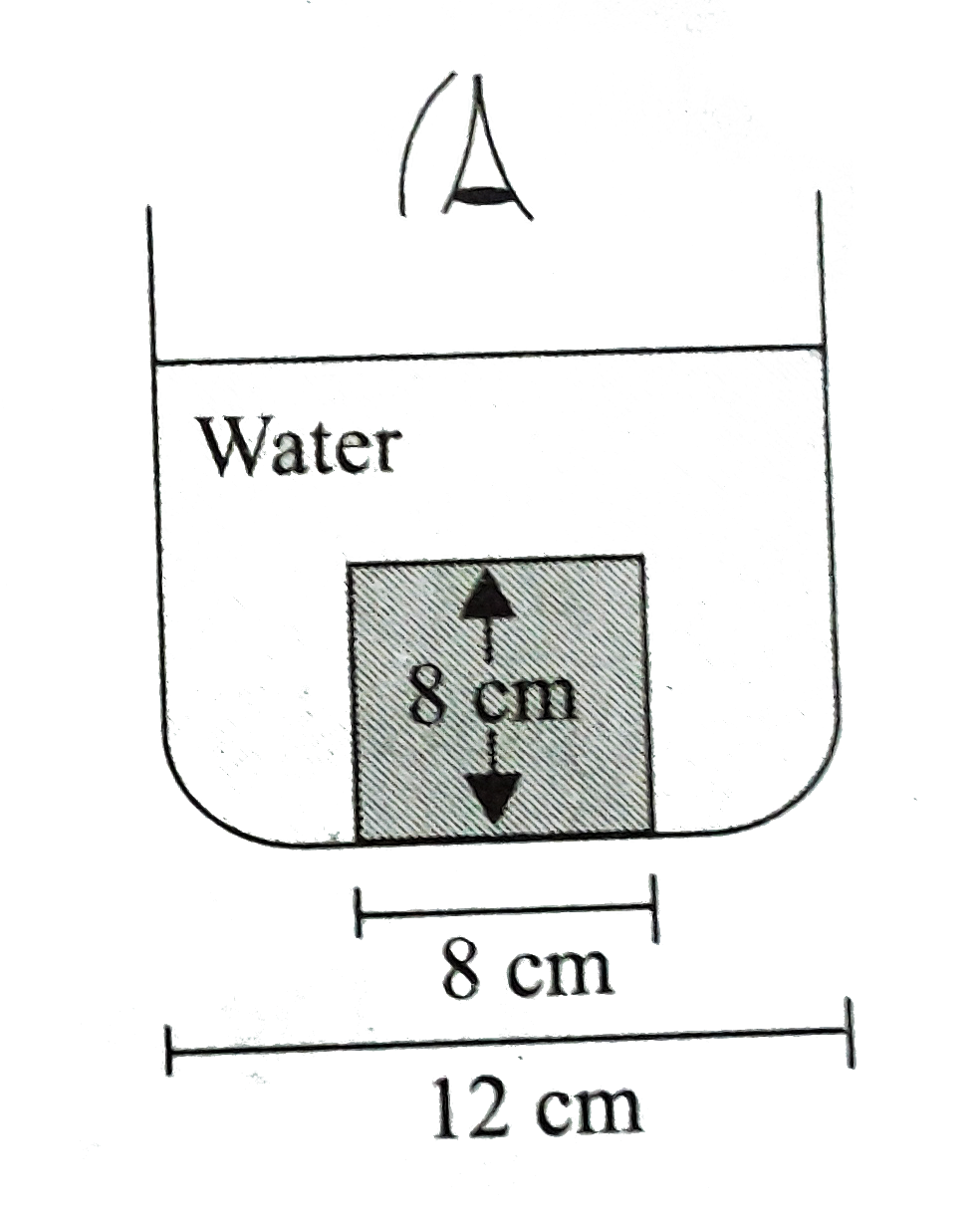
A cylindrical vessel of diameter 12 cm contains 800n cm 3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays (see figure 18-E6), locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.
 View Solution
View SolutionA cylindrical vessel of diameter 12 cm contains 800n cm 3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays (see figure 18-E6), locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical vessel of diameter 12 cm contains 800πcm3 of water. A cylindrical glass piece of diameter 8.0cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays, locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.
 A9.2 cm above the bottomB12.5cm above the bottomC7.1cm above th bottomD7.1 cm below the bottom
A9.2 cm above the bottomB12.5cm above the bottomC7.1cm above th bottomD7.1 cm below the bottom - Question 2 - Select One
A cone of radius 3.5 cm and height 12 cm is completely filled with water. This water is emptied into an empty cylindrical vessel of radius 7 cm. What will be the height of water in this vessel ?
A2 cmB0.33 cmC0.5 cmD1 cm - Question 3 - Select One
3 ice cubes of side π cm when dropped into a cylindrical glass of base diameter 2π cm increase the level of water in the glass by 3 cm.
A(i)(ii)(iii)(iv)FTTFB(i)(ii)(iii)(iv)TTFFC(i)(ii)(iii)(iv)TFTTD(i)(ii)(iii)(iv)TFTF
A glass is in the shape of a cylinder of radius 7 cm and height 10 cm. Find the volume of juice in litre required to fill 6 such glasses. [Use π=227]
View SolutionA conical vessel with radius 10 cm and height 15 cm is completely filled with water. This water is poured into a cylinder with radius 5 cm. Find the height of water in the cylinder.
View SolutionA glass piece is dipped in a liquid of refractive index 43 it gets disappeared in the liquid. The refractive index of the glass piece is?
View SolutionA conical vessel whose internal radius is 10 cm and height 72 cm is full of water . If this water is poured into a cylindrical vessel with internal radius 30 cm, the height of the water level rises in it is :
View SolutionA conical vessel whose internal radius is 10 cm and height 72 cm is full of water . If this water is poured into a cylindrical vessel with internal radius 30 cm, the height of the water level rises in it is :
View Solution
