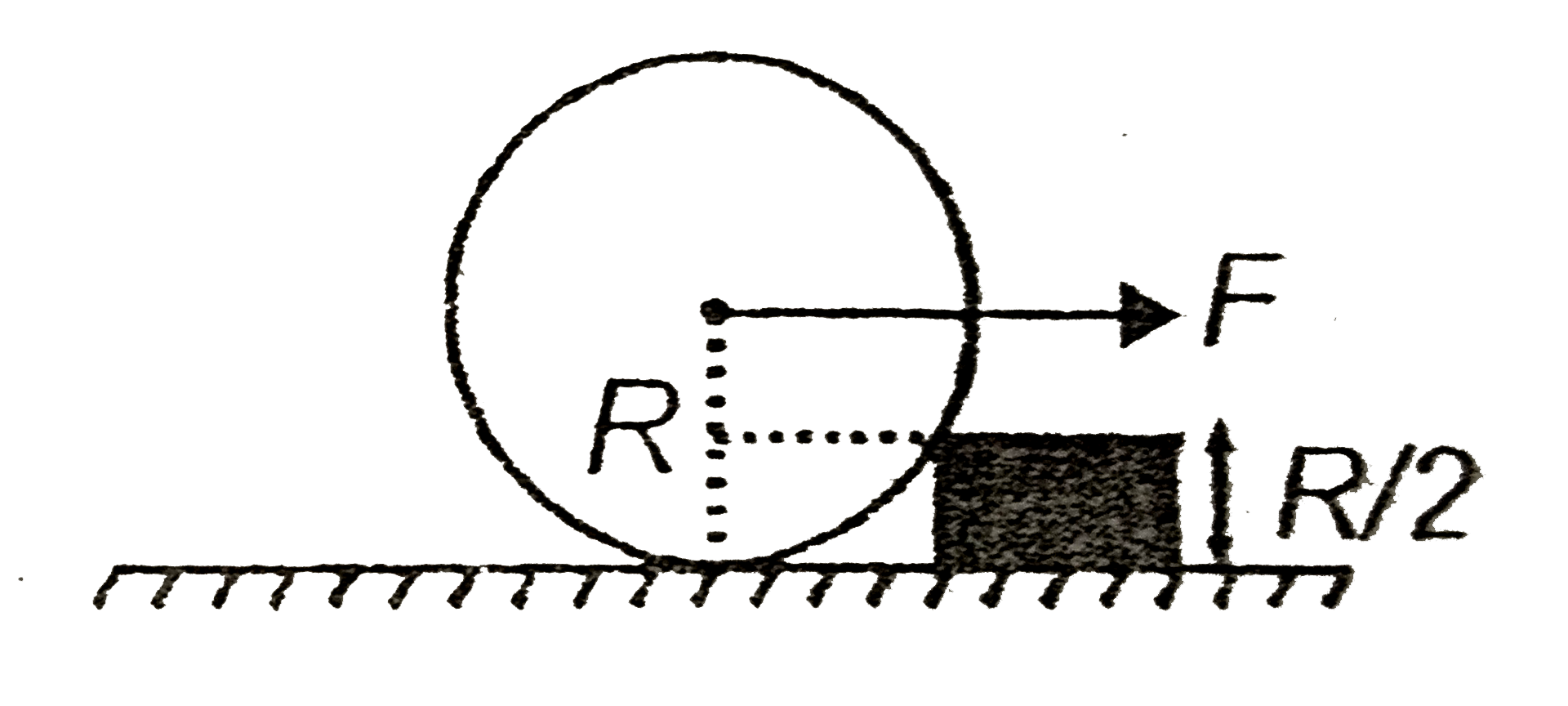
There is an obstruction of height h in front of a wheel of radius r weighing W. What is the minimum horizontal force that is to be applied at the centre O of the wheel to overcome the obstruction? Given, h <r.
The wheel touches the obstacle at point B Fig. Suppose a force F attempts to turn the wheel about the point B. Weight of wheel W , on the other hand, resists this rotation. Hence to overcome the obstacle moment of the force F about B must be greater than the moment of W about B.
For F to be minimum,
F×BD=W×BC
Here, BD = OC = OA-AC=r-h
BC = √OB2−OC2=√r2−(r−h)2=√2rh−h2
Hence, F (r-h) = W√2rh−h2
or, F = W√2rh−h2r−h.

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
Knowledge Check
A wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is
 Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghr
Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghrA heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
A20kgwtB1kgwtC10√3kgwtD10√2kgwtA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Vhoose the correct alternative.
 ASphere will always slide whatever be the value of hBSphere will roll without sliding when h≥104RCSphere will roll without sliding if h=1.4RDNone of the above
ASphere will always slide whatever be the value of hBSphere will roll without sliding when h≥104RCSphere will roll without sliding if h=1.4RDNone of the above
A solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View Solution