Thin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.

Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.

III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
The average human eye sees colors with wavelength between 430 nm to 680 nm. For what visible wavelength (s) will a 350 nm thick (n=1.35) soap film produce maximum destructive interference?
945 nm
473 nm
315 nm
None of these
The correct Answer is:b
Choices (a) and (c ) are eliminated immediately since are outside the visible range. For soap, nair>nsoap. The reflected wave, ray a, undergoes a phase change at the air-soap water interface. Ray Rb does not change phase at the soapy water-air interface. Based on interface reflections, the two rays are out of phase. To maintain this, the optical path difference, 2t, must not produce a phase change in Rb. Therefore, the path must be an integer multiple of λ
2t=mλ/n⇒λ=2tn/m=2(35nm)(1.35)/m=945/m
For m=1,λ=945nm
For m=2,λ=473nm [this is choice (b)]
For m=3,λ=315nm
Choice (b), λ=473nm, is the only choice in the visible range.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
View SolutionA light wave of frequency 5×1014Hz enters a medium of refractive index 1.5. In the velocity of the light wave is ….. And its wavelength is ……
View SolutionStatement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zero
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
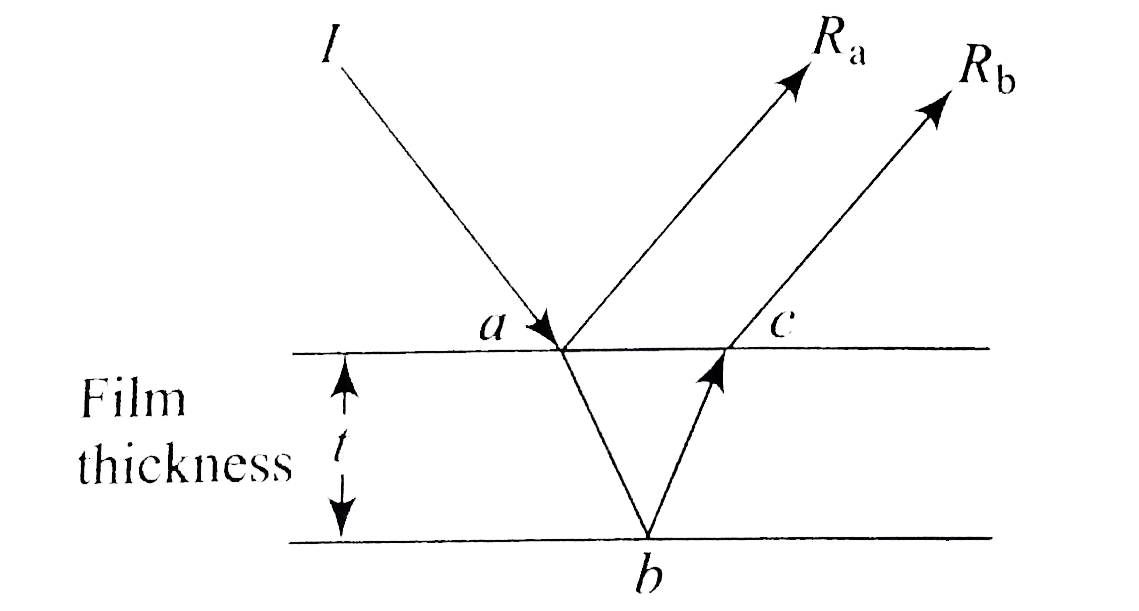
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.

III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
72. A film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
A thin film with index of refraction 1.33 coats a glass lens with index of refraction 1.50. Which of the following choices is the smallest film thickness that will not reflect light with wavelength 640 nm?
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
A soap film of thickness t is surrounded by air and is illuminated at near normal incidence by noonochromatic light wavelength λ in the film. With respect to the wavelength of the monochromatic ligth in the film, what film thickness will produce maximum consturctive interference
View SolutionThin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted. * When incident light, reaches the surface at point a, some of the light is reflected as ray R_(a) and and some is refracted following the path ab to the back of the film. *At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray R_(c) . R_(a) and R_(c) are parallel. However, R_(c) has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if R_(a) and R_(c) are in phase they will undergo constructive interference and the region ac will be bright if R_(a) and R_(c) are out of phase, they will undergo destructive interference. * Refraction at an interface never changes the phase of the wave. * For reflection at the interface between two media 1 and 2, if n_(1)ltn_(2) the reflected wave will change phase by pi . if n_(1)gtn_(2) the reflected wave will not undergo a phase change. for reference n_(air)=1.00 * if the waves are in phase after refection at all interfaces, then the effects of path length in the film are Constructive interference occur when (n= refractive index) 2t=mlamda//n" "m=0,1,2,3... .. Destructive interference occurs when 2t=(m+1//2)lamda//n" "m=0,1,2,3... Q. The average human eye sees colors with wavelengths between 430 nm to 680 nm. For what visible wavelength will a 350 nm thick n=1.35 soap film produce maximum destructive interference?
View SolutionThin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted. * When incident light, reaches the surface at point a, some of the light is reflected as ray R_(a) and and some is refracted following the path ab to the back of the film. *At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray R_(c) . R_(a) and R_(c) are parallel. However, R_(c) has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if R_(a) and R_(c) are in phase they will undergo constructive interference and the region ac will be bright if R_(a) and R_(c) are out of phase, they will undergo destructive interference. * Refraction at an interface never changes the phase of the wave. * For reflection at the interface between two media 1 and 2, if n_(1)ltn_(2) the reflected wave will change phase by pi . if n_(1)gtn_(2) the reflected wave will not undergo a phase change. for reference n_(air)=1.00 * if the waves are in phase after refection at all interfaces, then the effects of path length in the film are Constructive interference occur when (n= refractive index) 2t=mlamda//n" "m=0,1,2,3... .. Destructive interference occurs when 2t=(m+1//2)lamda//n" "m=0,1,2,3... Q. A 600 nm light is perpendicularly incident on a soap film suspended in air. The film is 1.00 mum thick with n=1.35. Which statement most accurately describes the interference of the light reflected by the two surfaces of the film?
View SolutionWhat is the phase difference between two successive crests in the wave
View SolutionTwo waves of equal amplitude when superposed, give a resultant wave having an amplitude equal to that of either wave. The phase difference between the two waves is
View SolutionWhat is the phase difference between consecutive crest and through ?
View SolutionWhat will be intensities of the waves whenthe waves interfere . In phase and
View SolutionWhen a crest of one wave coincides the crest of other wave, the resultant amplitude is maximum at the point, then that point looks:
View SolutionExplain the terms crest and trough of a wave.
View Solution




