Three arrangements are shown in figure.
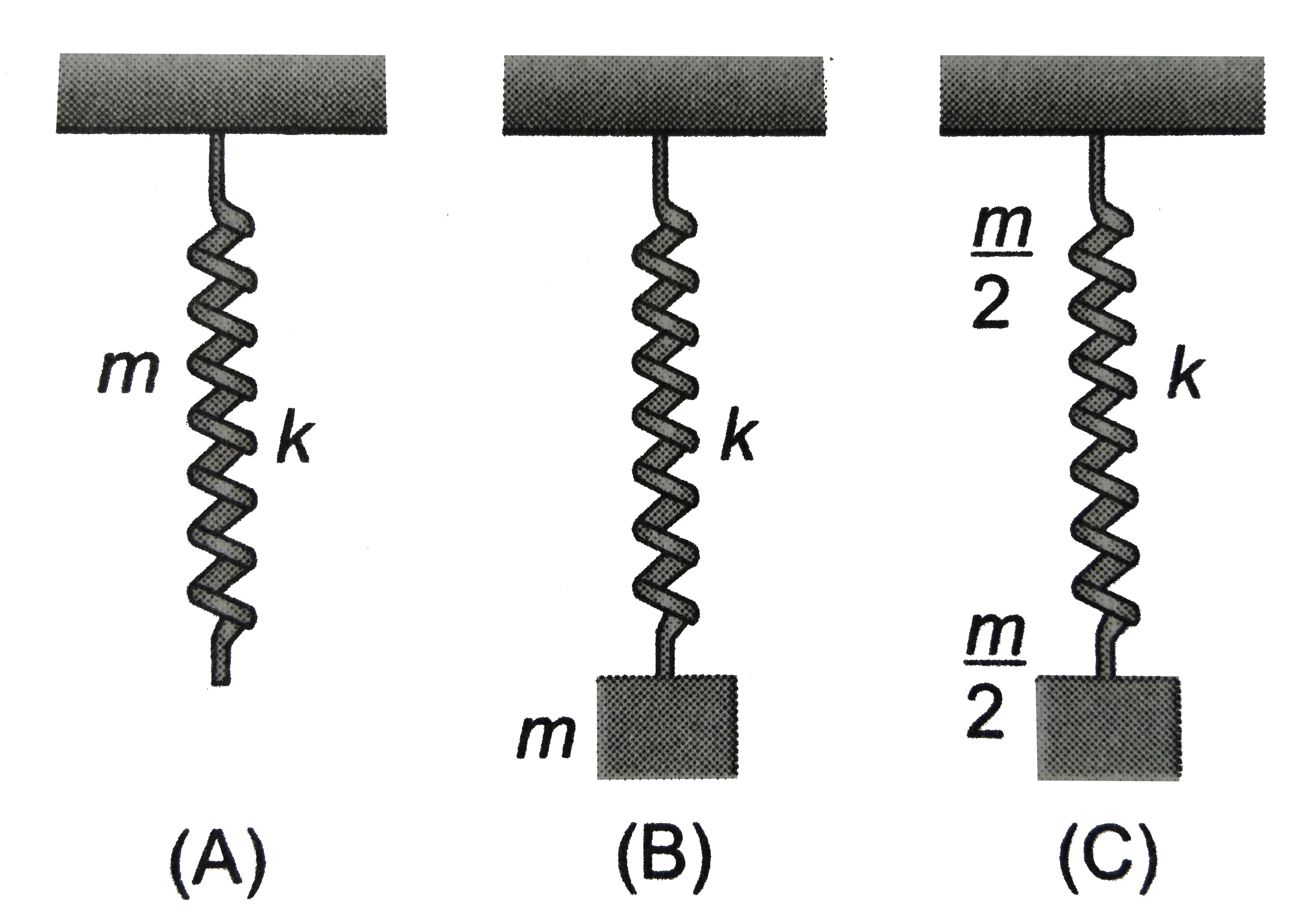
(a) A spring of mass m and stiffness k
(b) A block of mass m attached to massless spring of stiffness k
( c) A block of mass m2 attached to a spring of mass m2 and stiffness k
If T1, T2 and T3 represent the period of oscillation in the three cases respectively, then identify the correct relation.
T1<T2<T3
T1<T3<T2
T1>T3>T2
T3<T1<T2
The correct Answer is:B
T=2π√m+ms/3k(in general)
Here ms = mass of spring
and m = mass of block.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
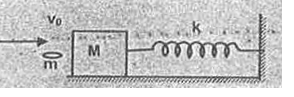
A bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.

View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
View Solution
Knowledge Check
Three arrangements of spring - mass system are shown in figures (A), (B) and ( C). If T1, T2 and T3 represent the respective periods of oscillation, then correct relation is
 AT1>T2>T3BT3>T2>T1CT2>T1>T3DT2>T3>T1
AT1>T2>T3BT3>T2>T1CT2>T1>T3DT2>T3>T1Calculate the period of oscillations of block of mass m attached with a set of springs as shown
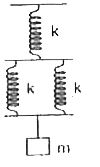 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these
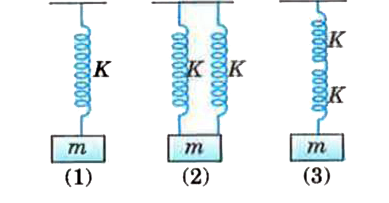
The figure shows the arrangement of block of mass m with one or more identical springs in three different ways . If Force cosntant of each springs is K and T1, T2 and T3 are the time periods of oscillations of the arrangement 1, 2, and 3, respectibely, then
View SolutionA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionA mass m is attached to two springs of same force constant K, as shown in following four arrangements. If T1,T2,T3andT4 respectively be the time periods of oscillation in the following arrangements in which case time period is maximum ?
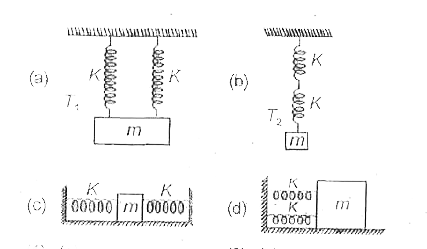
View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution
