Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
the field is zero but potential is non-zero
the field is non-zero but potential is zero
Both field and potential are zero
Both field and potential are non-zero
The correct Answer is:B
To solve the problem of finding the electric field and potential at the center of an equilateral triangle formed by three charges 2q, −q, and −q, we can follow these steps:
Step 1: Understand the Configuration
We have three charges located at the vertices of an equilateral triangle. Let's denote the vertices as A, B, and C:
- Charge at vertex A = 2q
- Charge at vertex B = −q
- Charge at vertex C = −q
Step 2: Determine the Center of the Triangle
The center of an equilateral triangle (also known as the centroid) is the point where the medians intersect. This point is equidistant from all three vertices.
Step 3: Calculate the Electric Field at the Center
The electric field E due to a point charge is given by the formula:
E=14πϵ0Qr2
where Q is the charge and r is the distance from the charge to the point where the field is being calculated.
1. Electric Field due to Charge 2q:
- The electric field at the center O due to charge 2q will point away from the charge since it is positive.
2. Electric Field due to Charge −q at Vertex B:
- The electric field at O due to charge −q will point towards the charge because it is negative.
3. Electric Field due to Charge −q at Vertex C:
- Similar to charge at B, the electric field at O due to charge −q will also point towards the charge.
Since the two −q charges are symmetrically located with respect to the center, their electric fields will have components that cancel each other in the horizontal direction (if we assume the triangle is oriented with one side horizontal). The vertical components will add up.
Step 4: Resultant Electric Field
The resultant electric field at the center O will not be zero because the contributions from the two −q charges will add up, while the contribution from 2q will also point in the same direction. Therefore, the electric field at the center is non-zero.
Step 5: Calculate the Electric Potential at the Center
The electric potential V due to a point charge is given by:
V=14πϵ0Qr
1. Potential due to Charge 2q:
V2q=14πϵ02qr
2. Potential due to Charge −q at Vertex B:
V−q=14πϵ0−qr
3. Potential due to Charge −q at Vertex C:
V−q=14πϵ0−qr
Step 6: Total Electric Potential
The total potential V at the center O will be:
V=V2q+V−q+V−q=14πϵ0(2qr−qr−qr)=14πϵ0(2q−q−qr)=0
Conclusion
- The electric field at the center of the triangle is non-zero.
- The electric potential at the center of the triangle is zero.
Thus, the correct answer is that the electric field is non-zero but the potential is zero.
We have three charges located at the vertices of an equilateral triangle. Let's denote the vertices as A, B, and C:
- Charge at vertex A = 2q
- Charge at vertex B = −q
- Charge at vertex C = −q
The center of an equilateral triangle (also known as the centroid) is the point where the medians intersect. This point is equidistant from all three vertices.
The electric field E due to a point charge is given by the formula:
E=14πϵ0Qr2
where Q is the charge and r is the distance from the charge to the point where the field is being calculated.
- The electric field at the center O due to charge 2q will point away from the charge since it is positive.
2. Electric Field due to Charge −q at Vertex B:
- The electric field at O due to charge −q will point towards the charge because it is negative.
- Similar to charge at B, the electric field at O due to charge −q will also point towards the charge.
The resultant electric field at the center O will not be zero because the contributions from the two −q charges will add up, while the contribution from 2q will also point in the same direction. Therefore, the electric field at the center is non-zero.
The electric potential V due to a point charge is given by:
V=14πϵ0Qr
V2q=14πϵ02qr
V−q=14πϵ0−qr
V−q=14πϵ0−qr
The total potential V at the center O will be:
V=V2q+V−q+V−q=14πϵ0(2qr−qr−qr)=14πϵ0(2q−q−qr)=0
- The electric field at the center of the triangle is non-zero.
- The electric potential at the center of the triangle is zero.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
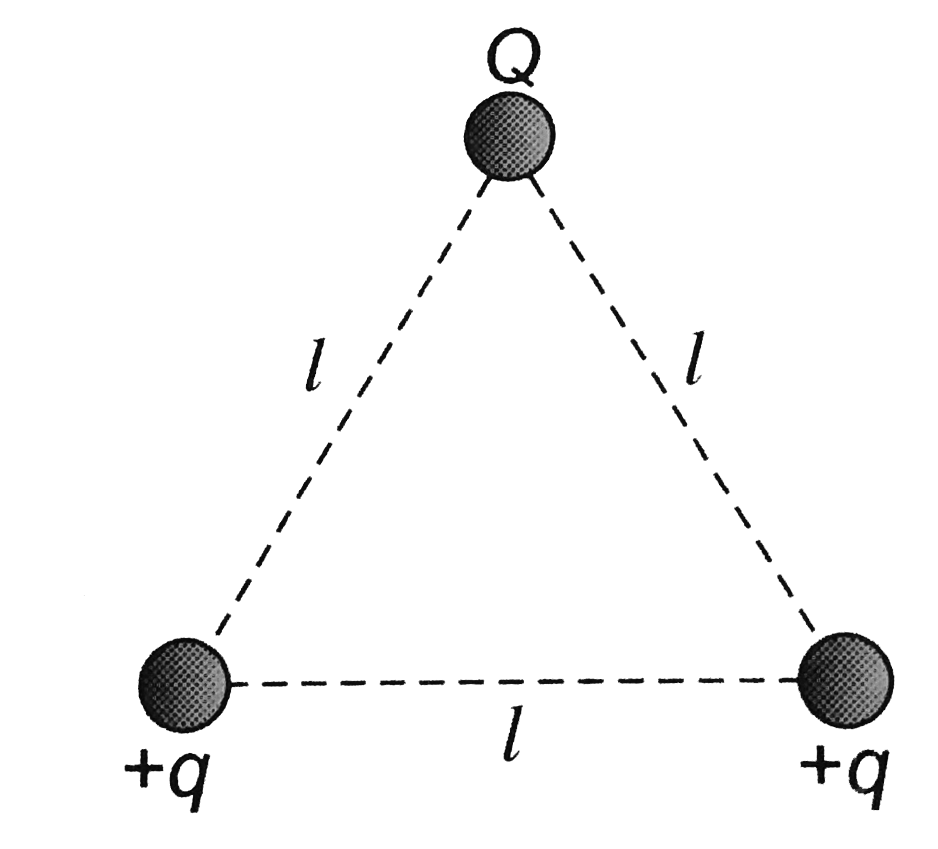
View Solution
Knowledge Check
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.
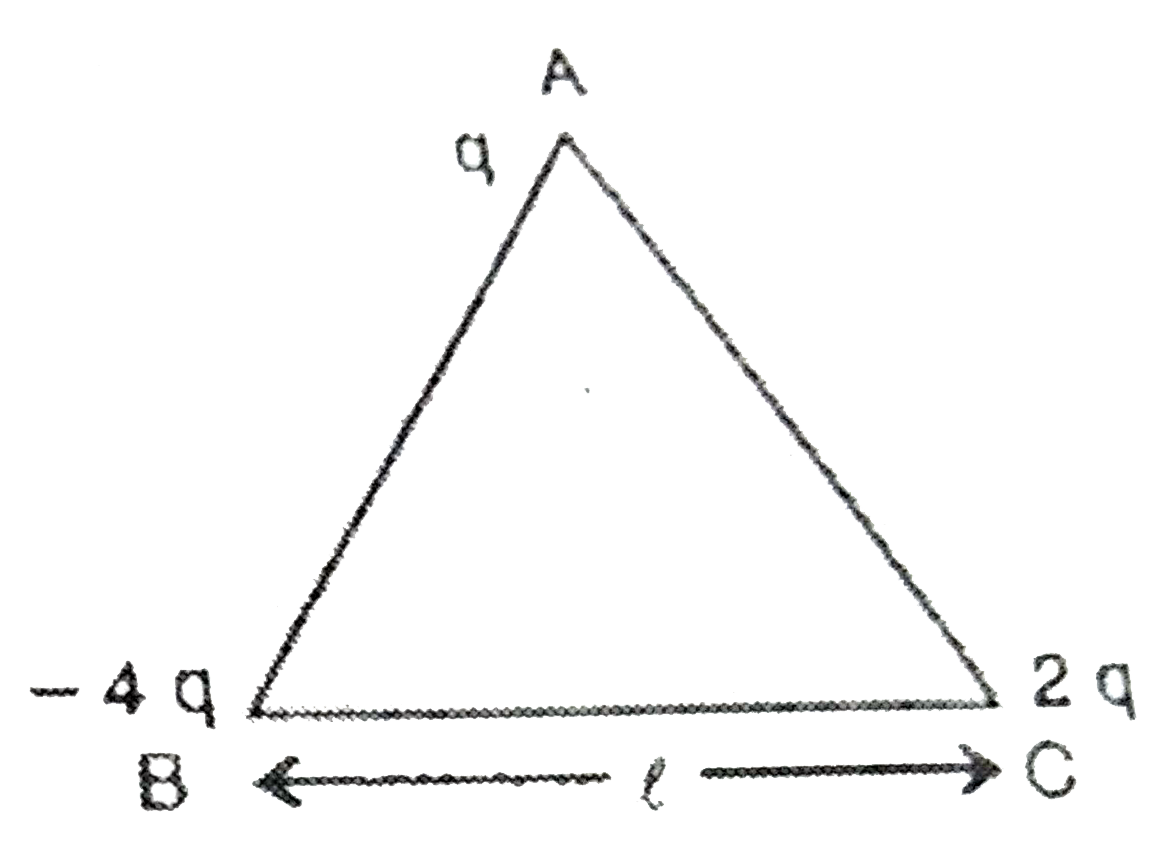
View SolutionThree poistive charges of equal value q are placed at the vertices of an equilateral triangle. The resulting lines of force should be sketched as in
View SolutionThree charges +q, -q and +q are kept at the corners of an equilateral triangle of side d. Find the resultant electric force on a charge +q placed at the centroid O of the triangle.
View SolutionThe point charges −2q,−2q and +q are put on the vertices of an equilateral triangle of side a. Find the work done by some external force in increasing the separation to 2a (in joules).
View SolutionThree charges Q0,−q and −q are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if Q 0 is equal to :
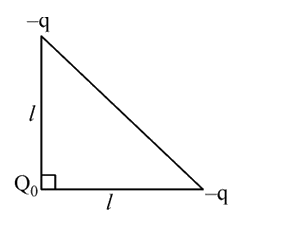
View Solution
