Three charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
To find the electrostatic potential at a point equidistant from the three corners of an equilateral triangle with charges placed at those corners, we can follow these steps:
1. Identify the Charges and Geometry:
- The charges are Q1=1nC=1×10−9C
- Q2=2nC=2×10−9C
- Q3=3nC=3×10−9C
- The side length of the equilateral triangle is a=√3m.
2. Determine the Distance from the Charges to the Point:
- The point equidistant from the three corners of the triangle is the centroid of the triangle.
- The distance from each vertex of the triangle to the centroid can be calculated as:
R=a√3=√3√3=1m
3. Calculate the Electrostatic Potential:
- The electrostatic potential V due to a point charge is given by:
V=kQr
where k=9×109N m2/C2 is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point of interest.
4. Calculate the Total Potential at the Centroid:
- The total potential Vnet at the centroid due to all three charges is the sum of the potentials due to each charge:
Vnet=V1+V2+V3
- Substituting the values:
V1=kQ1R=9×1091×10−91=9V
V2=kQ2R=9×1092×10−91=18V
V3=kQ3R=9×1093×10−91=27V
5. Sum the Potentials:
- Now, add the potentials:
Vnet=V1+V2+V3=9V+18V+27V=54V
Final Answer:
The electrostatic potential at the point equidistant from the three corners of the triangle is Vnet=54V.
- The charges are Q1=1nC=1×10−9C
- Q2=2nC=2×10−9C
- Q3=3nC=3×10−9C
- The side length of the equilateral triangle is a=√3m.
- The point equidistant from the three corners of the triangle is the centroid of the triangle.
- The distance from each vertex of the triangle to the centroid can be calculated as:
R=a√3=√3√3=1m
- The electrostatic potential V due to a point charge is given by:
V=kQr
where k=9×109N m2/C2 is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point of interest.
- The total potential Vnet at the centroid due to all three charges is the sum of the potentials due to each charge:
Vnet=V1+V2+V3
- Substituting the values:
V1=kQ1R=9×1091×10−91=9V
V2=kQ2R=9×1092×10−91=18V
V3=kQ3R=9×1093×10−91=27V
- Now, add the potentials:
Vnet=V1+V2+V3=9V+18V+27V=54V
The electrostatic potential at the point equidistant from the three corners of the triangle is Vnet=54V.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)17videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (ASSERTION REASON TYPE QUESTIONS)8videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Long Answer Questions)13videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Three charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
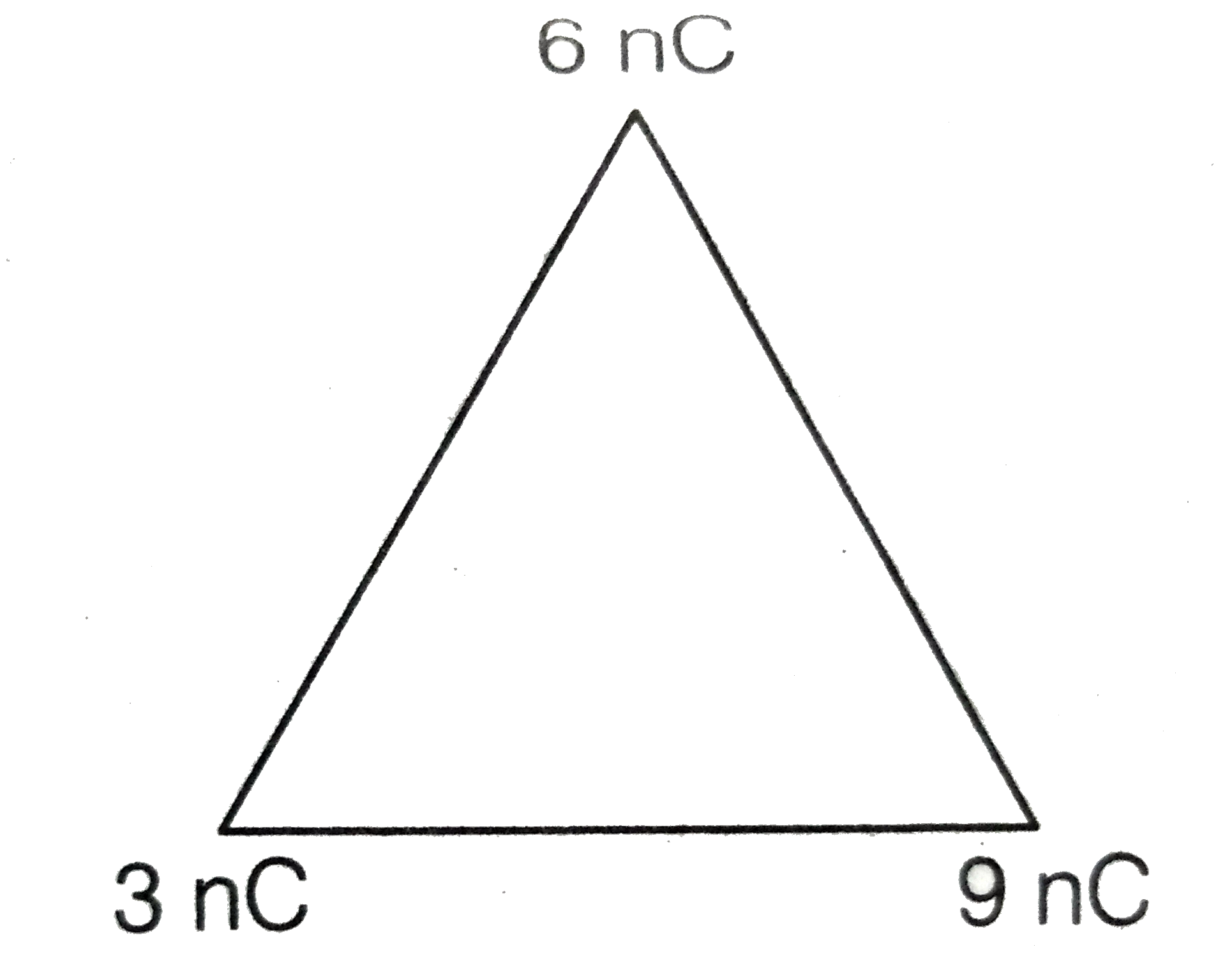
View SolutionThree point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27J - Question 2 - Select One
Charge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
A78 NB39 NC29 ND22.5 N
Three point charges of 1C, 2C and 3C are placed at the . corners of an equilateral triangle of side 1m. Calculate the work required to move these charges to the corners of a smaller equilateral triangle of side 1.5m.
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
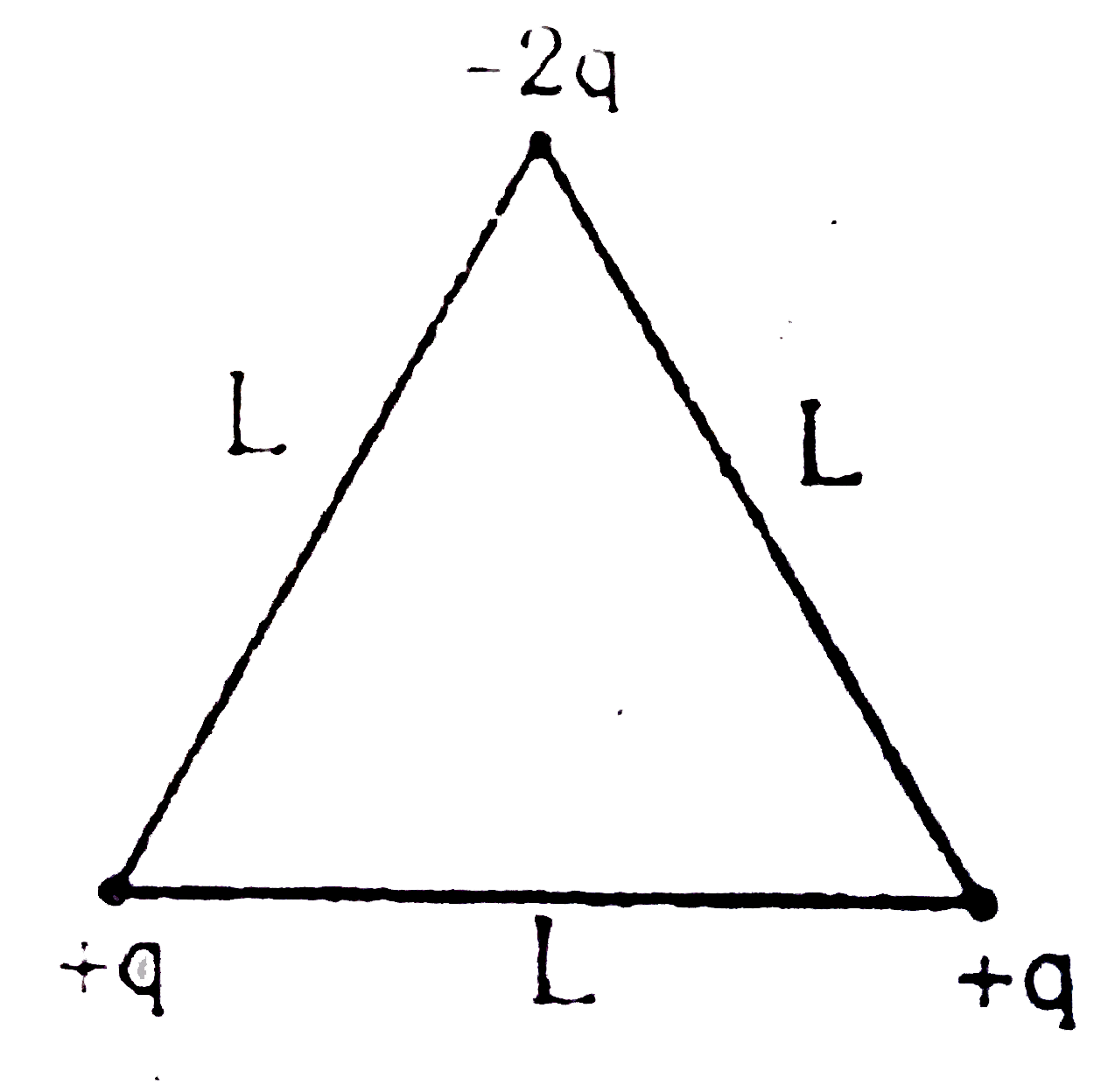
View SolutionThree points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
 View Solution
View SolutionThree charges −1μC,2μCand3νCare placed respectively at the corners A, B, C of an equiliateral triangle of sides 2m. Calculate the potential and electric field at the midpoint of the side BC.
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View Solution

