Three condensers each of capacity C microfarad are connected in series. An exactly similar set is connected in parallel to the first one. The effective capacity of the combination is 4μF. Then, the value of C in microfard is
8
6
4
2
The correct Answer is:B
To solve the problem, we need to find the value of C in microfarads given that three capacitors of capacity C each are connected in series, and another identical set is connected in parallel to the first one, resulting in an effective capacity of 4 µF.
1. Understand the Configuration:
- We have two sets of capacitors.
- Each set contains three capacitors (C) connected in series.
- The two sets are connected in parallel.
2. Calculate the Equivalent Capacitance for One Set in Series:
- For capacitors in series, the formula for equivalent capacitance (C_eq) is given by:
1Ceq=1C1+1C2+1C3
- Since all capacitors have the same capacitance C:
1Ceq=1C+1C+1C=3C
- Therefore, the equivalent capacitance for one set of three capacitors in series is:
Ceq=C3
3. Calculate the Equivalent Capacitance for Both Sets in Parallel:
- Since we have two sets of capacitors in series (each with capacitance C3) connected in parallel, the total equivalent capacitance (C_total) is:
Ctotal=Ceq1+Ceq2=C3+C3=2C3
4. Set Up the Equation:
- We are given that the effective capacity of the combination is 4 µF:
2C3=4
5. Solve for C:
- To find C, multiply both sides by 3:
2C=12
- Now, divide by 2:
C=6µF
Final Answer:
The value of C is 6 µF.
- We have two sets of capacitors.
- Each set contains three capacitors (C) connected in series.
- The two sets are connected in parallel.
- For capacitors in series, the formula for equivalent capacitance (C_eq) is given by:
1Ceq=1C1+1C2+1C3
- Since all capacitors have the same capacitance C:
1Ceq=1C+1C+1C=3C
- Therefore, the equivalent capacitance for one set of three capacitors in series is:
Ceq=C3
- Since we have two sets of capacitors in series (each with capacitance C3) connected in parallel, the total equivalent capacitance (C_total) is:
Ctotal=Ceq1+Ceq2=C3+C3=2C3
- We are given that the effective capacity of the combination is 4 µF:
2C3=4
- To find C, multiply both sides by 3:
2C=12
- Now, divide by 2:
C=6µF
The value of C is 6 µF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three.condensers of capacity 4mF,2mFand3mF are connected such that 2 mF and 3 mF are in series and 4 mF is parallel to them. The equivalent capacity of the combination is
View SolutionThree condensers of same capacity connected in series has effective capacity 2mF. If they are connected in parallel and charged using a battery of emf 12V, the total energy stored in the combination is
View SolutionFour capacitors are connected as shown in figure. Their capacities are indicated in the figure. The effective capacitance between points x and y is (in μF )

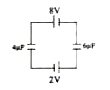
View SolutionTwo condensers of capacities 4mF and 6mF are connected to two cells as shown. Then
View SolutionTwo capacitors of capacitance C are connected in series. If one of them is filled with dielectric substance K, what is the effective capacitance?
View SolutionTwo inductors each of inductance L are connected in parallel. One more inductor of value 5 mH is connected in series of this configuration then the effective inductance is 15 mH . The value of L is ………..mH.
View SolutionA combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 Ω, find the resistance of the combination.
View SolutionTwo condensers of capacity 0.3μF and 0.6μF respectively are connected in series. The combination is connected across a potential of 6 volts. The ratio of energies stored by the condensers will be
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View Solution
