Three conducting spherical shells have radii (a, b, and c) such that a<b<c (Fig. 3.113). Initially, the inner shell is uncharged, the middle shell has a positive charge Q, and the outer shell has a negative charge −Q.
 .
.
a. Find the electric potential of the three shells.
b. If the inner and outer shells are now connected by a wire that is insulated as it passes through the middle shell, what is the electric potential of each of the three shells ? Also, what is the final charge on each shell ?
The correct Answer is:a. VA−VB=Q4πε0[c−bbc],VC=0
b. Charge on A−Qab[c−bc−a]
Charge on B,Qb=Q
Charge on C,Qcb[c−bc−a].
a. Potential of shell A
VA=Vdue to charge on A+Vdue to charge on B+Vdue to charge on C
=0+Q4πε0b−Q4πε0c
Potential of shell B
VB=Vdue to charge on A+Vdue to charge on B+Vdue to charge on C
=0+Q4πε0b−Q4πε0c
Potential of shell C
VC=Vdue to charge on A+Vdue to charge on B+Vdue to charge on C
=0+Q4πε0c−Q4πε0c=0
B After connecting inner and outer shells, we get
 .
.
VA=VC
or qa−qb+Q+qb−Q+qc=q−q+Q+q−(Q+q)c
or q=Qab(b−c)(c−a)
Final potential of A and C is zero.
VB=k[qa−qb+Q+qb−(Q+q)c]=k(Q+q)[c−bbc]
=k[Q+Qa(b−c)b(c−a)][c−bbc]=kQ[(b−a)(c−b)b2(c−a)].
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
In (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionThere are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
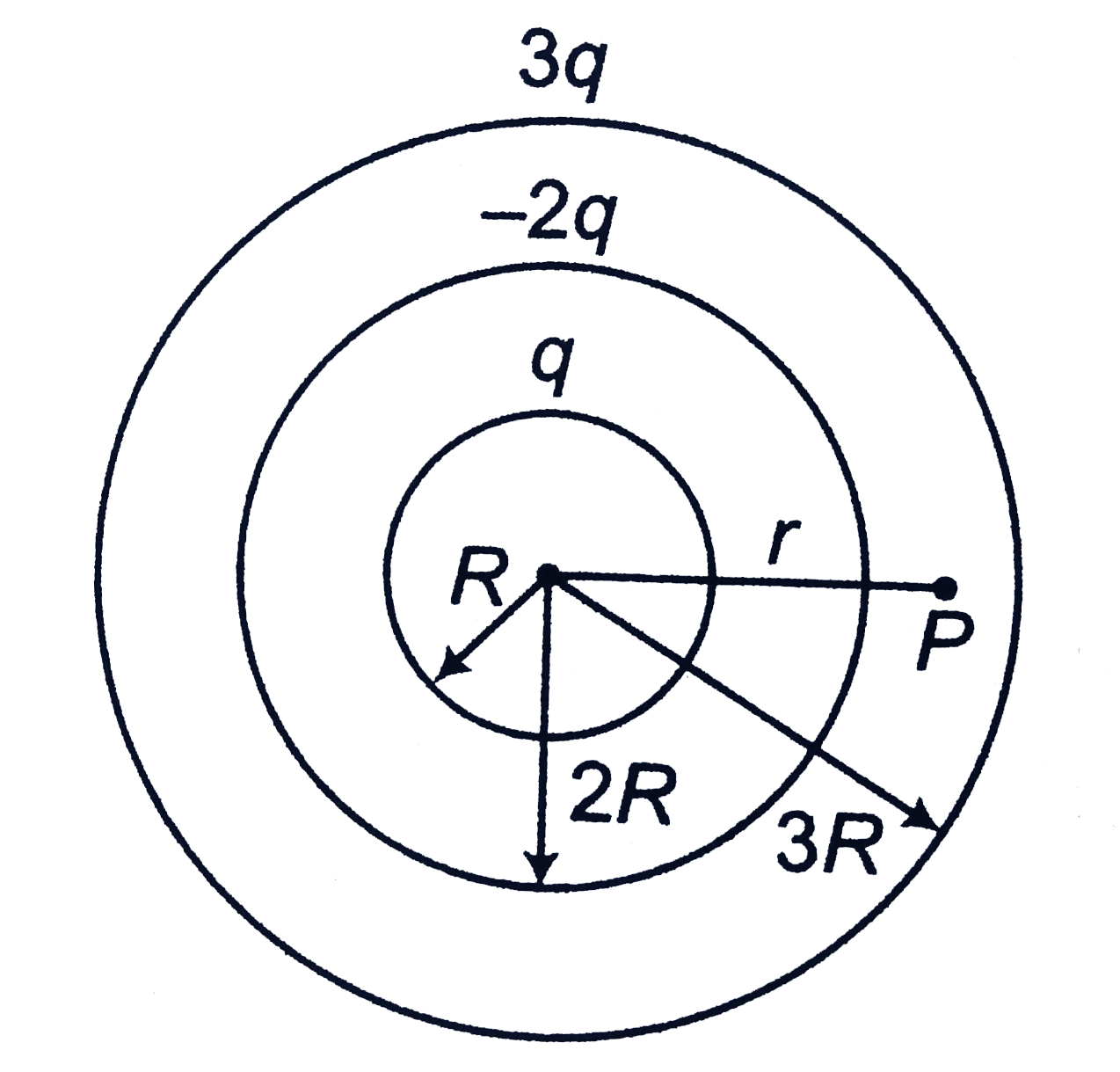
View SolutionThree conducting spherical shells have charges q,−2q and 3q as shown in figure. Find electric Potential at point P as shown in figure.
View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric in terms of q and the distance r from the common centre of the two shells for r>d.
View SolutionIn Fig a conducting spherical shell of inner radius .x. and outer radius .y. is concentric with a larger conducting spherical shell of inner radius .a. and outer radius .b.. Inner shell has a total charge +3Q and the outer shell has a charge +5Q. Let r be the distance of any point from the common centre O.

View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View Solution
