Three equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
If a fourth particle of equal mass is placed at the centre of triangle, then net force acting on it, is equal to
Gm2a2
4Gm23a2
3Gm2a2
zero
The correct Answer is:D
To solve the problem, we need to determine the net gravitational force acting on a mass placed at the center of an equilateral triangle formed by three other equal masses at its corners.
1. Understand the Configuration:
We have three equal masses (each of mass 'm') located at the vertices of an equilateral triangle with side length 'a'. A fourth mass (also of mass 'm') is placed at the center of this triangle.
2. Determine the Distance from the Center to a Vertex:
The distance from the center of the triangle to any vertex can be calculated using geometry. For an equilateral triangle, this distance (R) can be derived as:
R=a√3
This is because the center divides the median in a 2:1 ratio, and using trigonometric relationships, we find that the distance from the center to a vertex is a√3.
3. Calculate the Gravitational Field at the Center:
The gravitational field (E) due to one mass at the center is given by the formula:
E=GmR2
Substituting R=a√3:
E=Gm(a√3)2=Gm⋅3a2=3Gma2
Since there are three masses, the gravitational fields due to each mass will be directed towards the respective masses.
4. Components of the Gravitational Fields:
The gravitational fields due to the three masses will have both horizontal and vertical components. Due to symmetry, the horizontal components will cancel each other out. The vertical components will add up.
If we denote the gravitational field due to one mass as E:
- The vertical component of each gravitational field (pointing towards the center) can be calculated as:
Evertical=E⋅sin(30∘)=3Gma2⋅12=3Gm2a2
5. Net Gravitational Field at the Center:
Since there are three masses, the total vertical component of the gravitational field at the center will be:
Enet=3⋅Evertical=3⋅3Gm2a2=9Gm2a2
However, since the horizontal components cancel out, the net gravitational field at the center is:
Enet=0
6. Calculate the Gravitational Force on the Fourth Mass:
The gravitational force (F) acting on the mass at the center due to the net gravitational field is given by:
F=m⋅Enet=m⋅0=0
Final Answer:
The net force acting on the fourth mass placed at the center of the triangle is 0.
We have three equal masses (each of mass 'm') located at the vertices of an equilateral triangle with side length 'a'. A fourth mass (also of mass 'm') is placed at the center of this triangle.
The distance from the center of the triangle to any vertex can be calculated using geometry. For an equilateral triangle, this distance (R) can be derived as:
R=a√3
This is because the center divides the median in a 2:1 ratio, and using trigonometric relationships, we find that the distance from the center to a vertex is a√3.
The gravitational field (E) due to one mass at the center is given by the formula:
E=GmR2
Substituting R=a√3:
E=Gm(a√3)2=Gm⋅3a2=3Gma2
Since there are three masses, the gravitational fields due to each mass will be directed towards the respective masses.
The gravitational fields due to the three masses will have both horizontal and vertical components. Due to symmetry, the horizontal components will cancel each other out. The vertical components will add up.
- The vertical component of each gravitational field (pointing towards the center) can be calculated as:
Evertical=E⋅sin(30∘)=3Gma2⋅12=3Gm2a2
Since there are three masses, the total vertical component of the gravitational field at the center will be:
Enet=3⋅Evertical=3⋅3Gm2a2=9Gm2a2
However, since the horizontal components cancel out, the net gravitational field at the center is:
Enet=0
The gravitational force (F) acting on the mass at the center due to the net gravitational field is given by:
F=m⋅Enet=m⋅0=0
The net force acting on the fourth mass placed at the center of the triangle is 0.
Topper's Solved these Questions
Similar Questions
Three equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
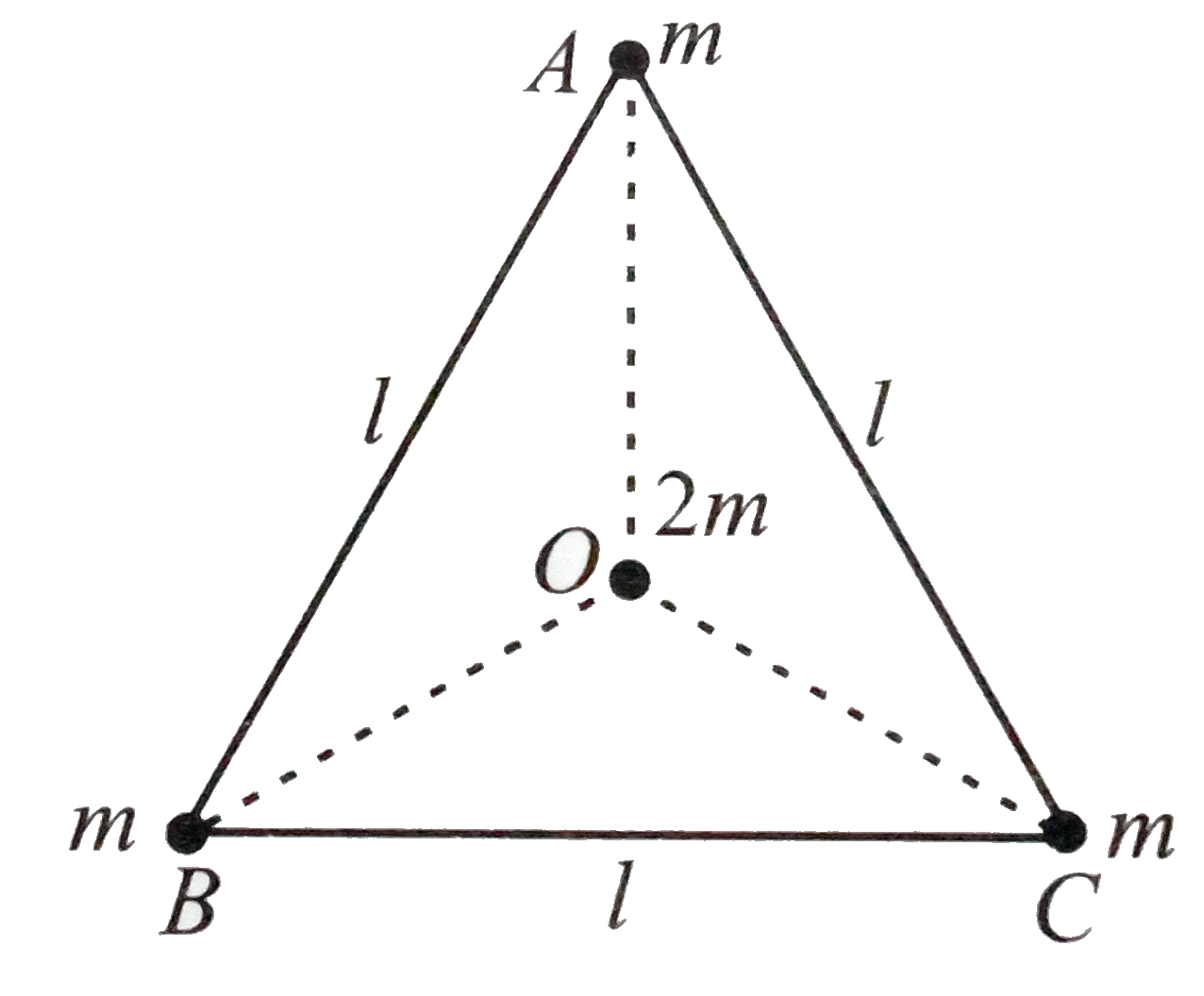 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
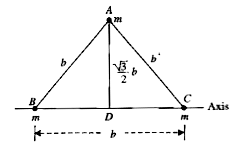 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree equal masses m are placed at the three corners of an equilateral triangle of side a. The force exerted by this system on another particle of mass m placed at the mid-point of a side.
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
In the above system, if two particles are kept fixed and third particle is released, then speed of the particle when it reaches to the mid point of the side connectiong other two masses is
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionThree equal masses m are placed at the three corners of an equilateral triangle of side a. find the force exerted by this system on another particle of mass m placed at (a) the mid point of a side (b) at the center of the triangle.
View Solution
