A particle is projected from the surface of earth of mass M and radius R with speed v. Suppose it travels a distance x(<<R) when its speed becomes v to v/2 and y(<<R) when speed changes from v/2 to 0. Similarly, the corresponding times are suppose t1andt2. Then
Column-IColumn-II(A)x/y(p)=1(B)t1/t2(r)>1(r)<1
The correct Answer is:A, B
To solve the problem, we need to analyze the motion of a particle projected from the surface of the Earth. We will use the equations of motion under uniform acceleration due to gravity.
Step 1: Analyze the first segment of motion (from speed v to v2)
1. Initial conditions:
- Initial speed, \( u = v \)
- Final speed, \( v' = \frac{v}{2} \)
- Acceleration, \( a = -g \) (negative because gravity acts downwards)
2. Using the equation of motion:
\(
v' = u - g t_1
\)
Substituting the values:
\(
\frac{v}{2} = v - g t_1
\)
Rearranging gives:
\(
g t_1 = v - \frac{v}{2} = \frac{v}{2}
\)
Thus,
\(
t_1 = \frac{v}{2g}
\)
3. Finding distance \( x \):
Using the second equation of motion:
\(
v'^2 = u^2 - 2g x
\)
Substituting the values:
\(
\left(\frac{v}{2}\right)^2 = v^2 - 2g x
\)
This simplifies to:
\(
\frac{v^2}{4} = v^2 - 2g x
\)
Rearranging gives:
\(
2g x = v^2 - \frac{v^2}{4} = \frac{3v^2}{4}
\)
Therefore,
\(
x = \frac{3v^2}{8g}
\)
Step 2: Analyze the second segment of motion (from speed v2 to 0)
1. Initial conditions:
- Initial speed, \( u = \frac{v}{2} \)
- Final speed, \( v' = 0 \)
2. Using the equation of motion:
\(
0 = \frac{v}{2} - g t_2
\)
Rearranging gives:
\(
g t_2 = \frac{v}{2}
\)
Thus,
\(
t_2 = \frac{v}{2g}
\)
3. Finding distance \( y \):
Using the second equation of motion:
\(
0 = \left(\frac{v}{2}\right)^2 - 2g y
\)
This simplifies to:
\(
0 = \frac{v^2}{4} - 2g y
\)
Rearranging gives:
\(
2g y = \frac{v^2}{4}
\)
Therefore,
\(
y = \frac{v^2}{8g}
\)
Step 3: Compare \( \frac{x}{y} \) and \( \frac{t_1}{t_2} \)
1. Calculating \( \frac{x}{y} \):
\(
\frac{x}{y} = \frac{\frac{3v^2}{8g}}{\frac{v^2}{8g}} = 3
\)
Thus, \( \frac{x}{y} = 3 > 1 \).
2. Calculating \( \frac{t_1}{t_2} \):
\(
\frac{t_1}{t_2} = \frac{\frac{v}{2g}}{\frac{v}{2g}} = 1
\)
Thus, \( \frac{t_1}{t_2} = 1 \).
Conclusion
- From the calculations:
- \( \frac{x}{y} = 3 \) (greater than 1)
- \( \frac{t_1}{t_2} = 1 \)
Final Matching
- (A) \( \frac{x}{y} \) matches with (r) \( > 1 \)
- (B) \( \frac{t_1}{t_2} \) matches with (p) \( = 1 \)
- Initial speed, \( u = v \)
- Final speed, \( v' = \frac{v}{2} \)
- Acceleration, \( a = -g \) (negative because gravity acts downwards)
\(
v' = u - g t_1
\)
Substituting the values:
\(
\frac{v}{2} = v - g t_1
\)
Rearranging gives:
\(
g t_1 = v - \frac{v}{2} = \frac{v}{2}
\)
Thus,
\(
t_1 = \frac{v}{2g}
\)
Using the second equation of motion:
\(
v'^2 = u^2 - 2g x
\)
Substituting the values:
\(
\left(\frac{v}{2}\right)^2 = v^2 - 2g x
\)
This simplifies to:
\(
\frac{v^2}{4} = v^2 - 2g x
\)
Rearranging gives:
\(
2g x = v^2 - \frac{v^2}{4} = \frac{3v^2}{4}
\)
Therefore,
\(
x = \frac{3v^2}{8g}
\)
- Initial speed, \( u = \frac{v}{2} \)
- Final speed, \( v' = 0 \)
\(
0 = \frac{v}{2} - g t_2
\)
Rearranging gives:
\(
g t_2 = \frac{v}{2}
\)
Thus,
\(
t_2 = \frac{v}{2g}
\)
Using the second equation of motion:
\(
0 = \left(\frac{v}{2}\right)^2 - 2g y
\)
This simplifies to:
\(
0 = \frac{v^2}{4} - 2g y
\)
Rearranging gives:
\(
2g y = \frac{v^2}{4}
\)
Therefore,
\(
y = \frac{v^2}{8g}
\)
\(
\frac{x}{y} = \frac{\frac{3v^2}{8g}}{\frac{v^2}{8g}} = 3
\)
Thus, \( \frac{x}{y} = 3 > 1 \).
\(
\frac{t_1}{t_2} = \frac{\frac{v}{2g}}{\frac{v}{2g}} = 1
\)
Thus, \( \frac{t_1}{t_2} = 1 \).
- \( \frac{x}{y} = 3 \) (greater than 1)
- \( \frac{t_1}{t_2} = 1 \)
- (B) \( \frac{t_1}{t_2} \) matches with (p) \( = 1 \)
Topper's Solved these Questions
Similar Questions
A particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V < escape velocity , g is the acceleration due to gravity on the surface of the earth )
View SolutionMatch the column :
A particle at a distance r from the centre of a uniform spherical planet of mass M radius R(<r) has a velocity v magnitude of which is given in column I. Match trajectory from column II about possible nature of orbit.
Column IColumn II(A)0<V<√GMr(P)Straight line(B)√GMr(Q)Circle(C)√2GMr(R)Parabola(D)v>√2GMr(S)Ellipse
View SolutionThe area of hole (1) is A1 and of hole (2) is A2. The velocity of efflux and range of liquid is v1,v2andx1,x2 for holes (1) and (2) respectively. The time taken by liquid, jet to reach the ground from holes (1) and (2) are t1andt2 respectively. Cross section of tank is very very large compared to size of holes.
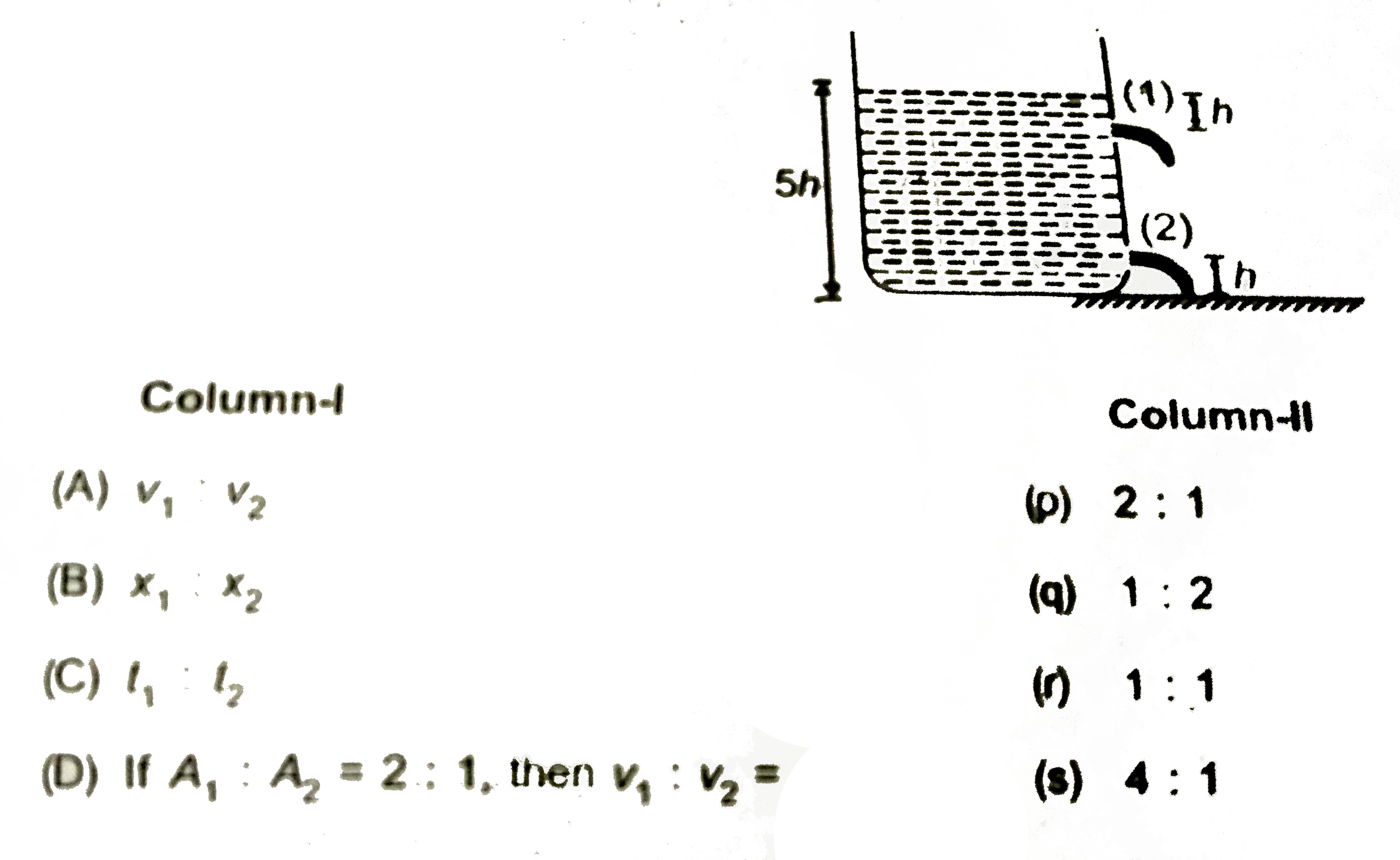
Column-IColumn-II(A)v1:v2(p)2:1(B)x1:x2(q)1:2(C)t1:t2(r)1:1(D)ifA1:A2=2:1,thenv1:v2=(s)4:1
View Solution_S01_038_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h(<<R) above the shell. There is a hole in the shell.
Q. With what approximate speed will it collide at B?
View Solution_S01_038_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h(<<R) above the shell. There is a hole in the shell.
Q. With what approximate speed will it collide at B?
View SolutionA person travels along a straight road for the first t3 time with a speed v1 and for next 2t3 time with a speed v2. Then the mean speed v is given by
View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight t1. If the same projectile is projected with same speed at another angle to have the saem range, time of flight is t2. Show that:
t1t2=(2R/g)
View SolutionTwo planets are at distance R1andR2 from the Sun. Their periods are T1andT2 then (T1T2)2 is equal to
View SolutionA particle is thrown up vertically with a speed v1 in air . If takes time t1 in upward journey and t2(>t1) in the downward journey and returns to the starting point with a speed v2. Then:-
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View Solution
