Three identical particles each of mass M move along a common circlar path of radius R under the mutual interaction of each other. The velocity of each particle is
√GMR√23
√GM√3R
√GM3R
√23GMR
The correct Answer is:B
To find the velocity of each of the three identical particles of mass M moving in a circular path of radius R under mutual gravitational interaction, we can follow these steps:
1. Understanding the System:
We have three identical particles, each of mass M, moving in a circular path of radius R. The particles exert gravitational forces on each other, and we need to find the velocity of each particle.
2. Configuration of the Particles:
The three particles will form the vertices of an equilateral triangle, with the center of the circle coinciding with the centroid of the triangle. The distance from the centroid to each vertex (the radius R) can be related to the side length A of the triangle.
3. Finding the Side Length of the Triangle:
The relationship between the radius R of the circumcircle and the side length A of the equilateral triangle is given by:
R=A√3
Thus, we can express A in terms of R:
A=R√3
4. Calculating the Gravitational Force:
The gravitational force between any two particles (say A and B) is given by:
F=GM2A2
Substituting A=R√3:
F=GM23R2
5. Net Force Acting on a Particle:
Each particle experiences forces due to the other two particles. The net force acting towards the center of the circle can be calculated using vector addition. The angle between the forces due to two particles is 60∘. The net force Fnet can be calculated as:
Fnet=√F2+F2+2F⋅F⋅cos(60∘)=√F2+F2+F2=√3F
6. Centripetal Force Requirement:
For circular motion, the net force must equal the centripetal force required to keep the particle in circular motion:
Mv2R=√3F
Substituting F:
Mv2R=√3⋅GM23R2
7. Solving for Velocity v:
Rearranging the equation gives:
v2=√3GM3R⋅R=GM√3R
Taking the square root:
v=√GM√3R
Final Answer:
The velocity of each particle is:
v=√GM√3R
We have three identical particles, each of mass M, moving in a circular path of radius R. The particles exert gravitational forces on each other, and we need to find the velocity of each particle.
The three particles will form the vertices of an equilateral triangle, with the center of the circle coinciding with the centroid of the triangle. The distance from the centroid to each vertex (the radius R) can be related to the side length A of the triangle.
The relationship between the radius R of the circumcircle and the side length A of the equilateral triangle is given by:
R=A√3
Thus, we can express A in terms of R:
A=R√3
The gravitational force between any two particles (say A and B) is given by:
F=GM2A2
Substituting A=R√3:
F=GM23R2
Each particle experiences forces due to the other two particles. The net force acting towards the center of the circle can be calculated using vector addition. The angle between the forces due to two particles is 60∘. The net force Fnet can be calculated as:
Fnet=√F2+F2+2F⋅F⋅cos(60∘)=√F2+F2+F2=√3F
For circular motion, the net force must equal the centripetal force required to keep the particle in circular motion:
Mv2R=√3F
Substituting F:
Mv2R=√3⋅GM23R2
Rearranging the equation gives:
v2=√3GM3R⋅R=GM√3R
Taking the square root:
v=√GM√3R
The velocity of each particle is:
v=√GM√3R
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
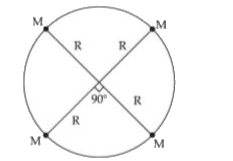
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
View SolutionTwo particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.

View Solution
Knowledge Check
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
AGmRB√2√2GMRC√GMR(2√2+1)D√GMR2√2+14Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
A√GM√2RB√GM√3RC√GM2RD√GM3R
For particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles of equal mass are moving round a circle of radius r due to their mutual gravitational attraction . Find the angular velocity of each particle .
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionTwo identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
View SolutionTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
View Solution
