A body of mass 2kg is moving under the influence of a central force whose potential energy is given by U=2r3J. If the body is moving in a circular orbit of 5m, its energy will be
625J
250J
500J
125J
The correct Answer is:A
To solve the problem, we need to find the total energy of a body of mass 2 kg moving in a circular orbit of radius 5 m under the influence of a central force with a given potential energy function U=2r3 J.
1. Identify the Potential Energy Function:
The potential energy U is given by:
U=2r3 J
2. Calculate the Force:
The force F associated with the potential energy can be found using the relation:
F=−dUdr
First, we differentiate U with respect to r:
dUdr=ddr(2r3)=6r2
Therefore, the force is:
F=−6r2
3. Centripetal Force Requirement:
For an object moving in a circular orbit, the centripetal force required is given by:
Fc=mv2r
Setting the magnitude of the gravitational force equal to the centripetal force:
mv2r=6r2
4. Express mv2:
Rearranging the equation gives:
mv2=6r3
5. Calculate Kinetic Energy:
The kinetic energy K is given by:
K=12mv2
Substituting mv2=6r3:
K=12(6r3)=3r3
6. Calculate Potential Energy:
The potential energy at radius r is:
U=2r3
7. Total Energy:
The total energy E is the sum of kinetic and potential energy:
E=K+U=3r3+2r3=5r3
8. Substituting r=5 m:
Now, substituting r=5 m into the total energy equation:
E=5(53)=5(125)=625 J
Final Answer:
The total energy of the body is 625 Joules.
---
The potential energy U is given by:
U=2r3 J
The force F associated with the potential energy can be found using the relation:
F=−dUdr
First, we differentiate U with respect to r:
dUdr=ddr(2r3)=6r2
Therefore, the force is:
F=−6r2
For an object moving in a circular orbit, the centripetal force required is given by:
Fc=mv2r
Setting the magnitude of the gravitational force equal to the centripetal force:
mv2r=6r2
Rearranging the equation gives:
mv2=6r3
The kinetic energy K is given by:
K=12mv2
Substituting mv2=6r3:
K=12(6r3)=3r3
The potential energy at radius r is:
U=2r3
The total energy E is the sum of kinetic and potential energy:
E=K+U=3r3+2r3=5r3
Now, substituting r=5 m into the total energy equation:
E=5(53)=5(125)=625 J
The total energy of the body is 625 Joules.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct10videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective14videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective19videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
A particle of mass 3 kg is moving under the action of a central force whose potential energy is given by U(r) = 10r3 joule. For what energy and angular momentum will the orbit be a circle of radius 10 m ?
View SolutionA particle of mass 9 kg is moving under the action of a central force whose potential energy is given by U=10/r For what energy it will orbit a circle of radius 10 m ? Calculate the time period of this motion
View Solution
Knowledge Check
- Question 1 - Select One
A body with mass 2kg moves in one direction in the presence of a force which is described by the potential energy graph. If the body is released from rest at x=2m, then its speed when it crosses x=5m is :−
 AzeroB1ms−1C2ms−1D3ms−1
AzeroB1ms−1C2ms−1D3ms−1 - Question 2 - Select One
A body with mass 1kg moves in one direction in the presence of a force which is described by the potential energy graph. If the body is releasd from rest at x=2m, than its speed when it crosses x=5m, is (Neglect dissipative forces).
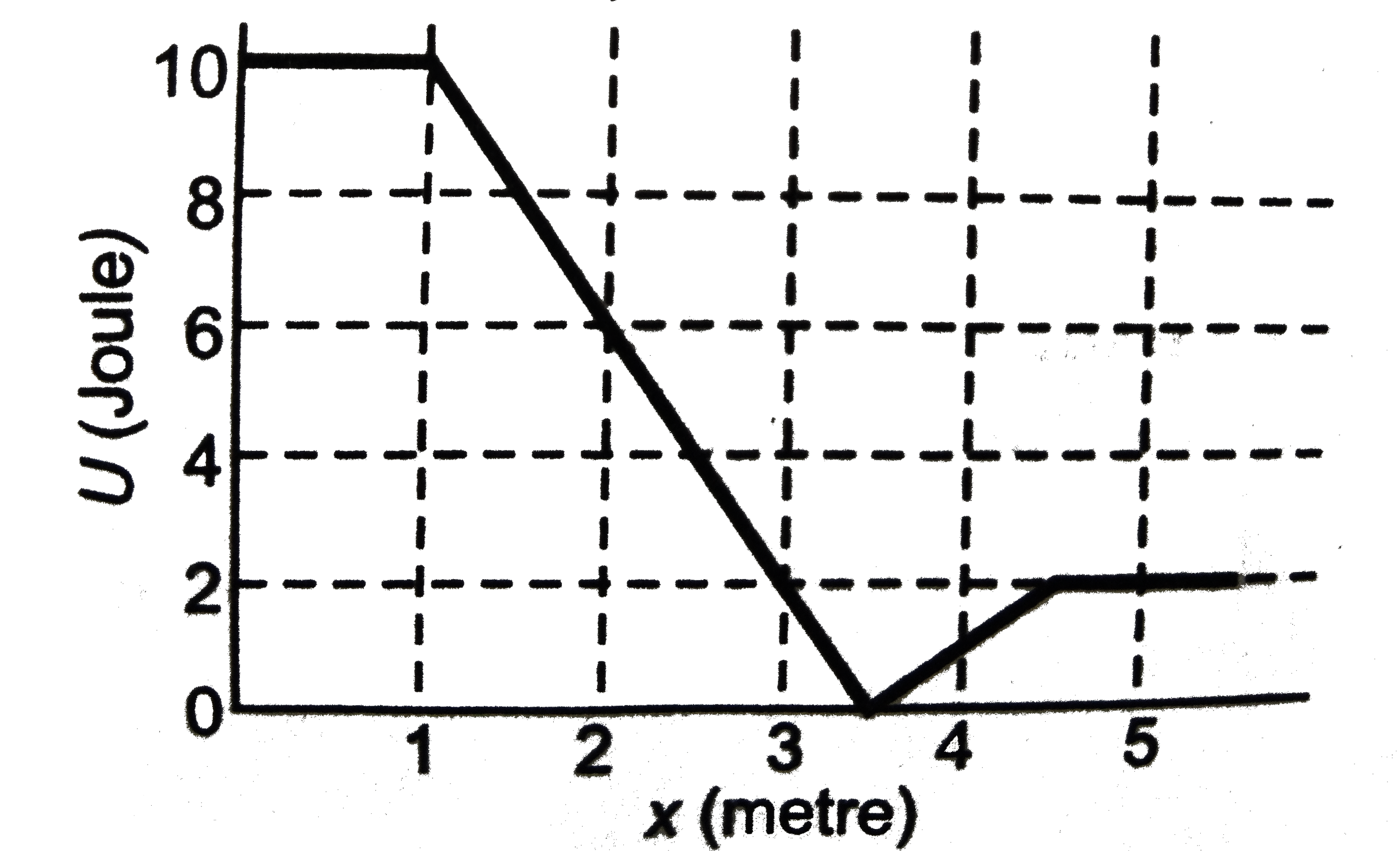 A2√2ms−1B1ms−1C2ms−1D3ms−1
A2√2ms−1B1ms−1C2ms−1D3ms−1 - Question 3 - Select One or More
A body of mass m is in a field where its potential energy is given by U=ax3+bx4, where a and b are positive constants. Then, [The body moves only along x]
Ax=0 is a point of equilibriumBx=−3a4b is a point of stable equilibriumCx=−3a4b is a point of unstable equilibriumDfor small displacements from stable equilibrium position the body executes SHM with angular frequency 3a2√bm
A body of mass 4kg moving along a straight line under the action of a force.If kinetic energy varies with time as k=8t .The force acting on the body is ?
View SolutionThe total energy of a satellite moving in a circular orbit is [−1.5×109J]. What is its bilding energy?
View SolutionA body of mass 2kg is projected vertically upwards with a speed of 3m/s. The maximum gravitational potential energy of the body is :
View SolutionThe potential energy of body of mass m given by U=px+qy+rz. The magnitude of the acceleration of the body will be
View SolutionA body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to-
View Solution

