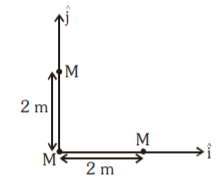
Three identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass

Text Solution

Verified by Experts

$x = \frac{m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}}{m_{1} + m_{2} + m_{3}}$
$∴ = \frac{(M \times 0) + (M \times 0) + (M \times 2)}{M + M + M} = \frac{2 M}{3 M} = \frac{2}{3} m$

$∴$ x-coordination = $2 / 3 \hat{i}$
Again $y = \frac{(M \times 2) + (M \times 0) + (M \times 0)}{M + M + M}$
or $y = \frac{2 M}{3 M} = \frac{2}{3}$ m
$∴$ y-coordinate = $2 / 3 \hat{j}$
$∴$ Position vector of centre of mass = $\frac{2}{3} \hat{i} + \frac{2}{3} \hat{j} = \frac{2}{3} (\hat{i} + \hat{j})$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
A $2 (ˆ i + ˆ j)$
B $(ˆ i + ˆ j)$
C $2 \frac{ˆ i + ˆ j}{3}$
D $4 \frac{ˆ i + ˆ j}{3}$
Question 2 - Select One
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
A(##PW_NEET_45_DAY_PHY_C06_E03_004_Q01##)
B $\frac{2}{3} (ˆ i + ˆ j)$
C $\frac{4}{3} (ˆ i + ˆ j)$
D $2 (ˆ i + ˆ j)$
Question 3 - Select One
Three equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
A $x = 5 cm, y = 5 cm$
B $x = \frac{5}{3} cm, y = 5 cm$
C $x = \frac{5}{3} cm, y = \frac{5}{2} cm$
D $x = \frac{5}{3} cm, y = \frac{5}{3} cm$

MTG GUIDE-MOTION OF SYSTEM OF PARTICLES AND RIGID BODY -AIPMT / NEET (MCQs)

Home
Ask Doubt
Profile