Three identical thin rods, each of mass $m$ and length $l$ , are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the moment of inertia of the equilateral triangular frame made of three identical thin rods about an axis parallel to one side and passing through the opposite vertex, we can follow these steps:
Step 1: Understand the Geometry of the Triangle
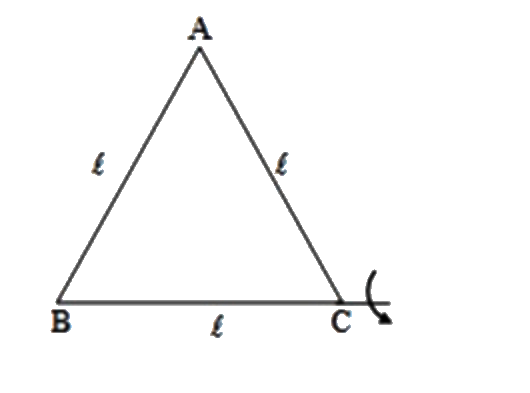
We have an equilateral triangle formed by three rods, each of mass $m$ and length $l$ . Let's denote the vertices of the triangle as $A$ , $B$ , and $C$ . The axis of rotation is parallel to side $A B$ and passes through vertex $C$ .
Step 2: Identify the Moment of Inertia Contributions
The moment of inertia $I$ about the axis can be calculated by considering the contributions from each rod:
- The rod $A C$ is perpendicular to the axis and will contribute to the moment of inertia.
- The rod $B C$ is also perpendicular to the axis and will contribute to the moment of inertia.
- The rod $A B$ is parallel to the axis, so its contribution to the moment of inertia about this axis is zero.
Step 3: Calculate the Moment of Inertia for Rods AC and BC
For a thin rod of length $l$ and mass $m$ about an axis through one end and perpendicular to its length, the moment of inertia is given by:
$I_{end} = \frac{1}{3} m l^{2}$
However, since we need the moment of inertia about the axis that is at a distance $h$ from the end of the rod, we will use the parallel axis theorem:
$I = I_{end} + m d^{2}$
where $d$ is the distance from the center of mass of the rod to the new axis.
Step 4: Determine the Distance $d$
For rods $A C$ and $B C$ :
- The distance $d$ from the center of mass of each rod to the axis is $\frac{l sin (60^{\circ})}{2} = \frac{l \sqrt{3}}{4}$ .
Step 5: Calculate Moment of Inertia for Rods AC and BC
Using the parallel axis theorem:
$I_{A C} = \frac{1}{3} m l^{2} + m {(\frac{l \sqrt{3}}{4})}^{2}$
Calculating this gives:
$I_{A C} = \frac{1}{3} m l^{2} + m \cdot \frac{3 l^{2}}{16} = \frac{1}{3} m l^{2} + \frac{3}{16} m l^{2}$
Finding a common denominator (48):
$I_{A C} = \frac{16}{48} m l^{2} + \frac{9}{48} m l^{2} = \frac{25}{48} m l^{2}$
Since $I_{B C}$ will be the same as $I_{A C}$ :
$I_{B C} = \frac{25}{48} m l^{2}$
Step 6: Total Moment of Inertia
The total moment of inertia $I$ about the axis is:
$I = I_{A C} + I_{B C} + I_{A B}$
Since $I_{A B} = 0$ :
$I = \frac{25}{48} m l^{2} + \frac{25}{48} m l^{2} = \frac{50}{48} m l^{2} = \frac{25}{24} m l^{2}$
Step 7: Calculate the Radius of Gyration
The radius of gyration $k$ is given by:
$k = \sqrt{\frac{I}{M}}$
where $M$ is the total mass of the system. The total mass $M = 3 m$ :
$k = \sqrt{\frac{\frac{25}{24} m l^{2}}{3 m}} = \sqrt{\frac{25 l^{2}}{72}} = \frac{5 l}{6 \sqrt{2}}$
Final Results
- The moment of inertia $I$ about the given axis is:
$I = \frac{25}{24} m l^{2}$
- The radius of gyration $k$ about the given axis is:
$k = \frac{5 l}{6 \sqrt{2}}$

Three indentical thin rods each of mass m and length L are joined together to form an equilateral triangular frame . The moment of inertia of frame about an axis perpendicular to the palne of frame and apssing through a corner is
A $\frac{2 m L^{2}}{3}$
B $\frac{3 m L^{2}}{2}$
C $\frac{4 m L^{2}}{3}$
D $\frac{3 m L^{2}}{4}$
Three identical rods, each of mass $m$ and length $l$ , form an equaliteral triangle. Moment of inertia about one of the sides is

A $\frac{m l^{2}}{6}$
B $m l^{2}$
C $\frac{3 m l^{2}}{4}$
D $\frac{2 m l^{2}}{3}$
Three identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
A $\frac{1}{6} M l^{2}$
B $\frac{1}{4} M l^{2}$
C $\frac{2}{3} M l^{2}$
D $\frac{4}{3} M l^{2}$